НАХОЖДЕНИЕ КВАДРАТУРЫ КРУГА В КЛАССИЧЕСКОЙ ГЕОМЕТРИИ С НАИБОЛЬШЕЙ ТОЧНОСТЬЮ И РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ

 Скачать статью в формате PDF

В статье автора [1] была поставлена и решена задача: найти квадратуру круга в рамках классической геометрии. В настоящей статье эта же задача решается с наибольшей точностью.
В классической геометрии все построения выполняются простой линейкой, не имеющей шкалы, и циркулем. Расстояния измеряются раствором циркуля.

Дано: Круг произвольного диаметра (Рис. 1а).
Задача: С помощью простой линейки и циркуля построить квадрат, площадь которого равна площади данного круга.
Решение:

1. Разбиение круга на четыре квадранта.

Если центр окружности, включающей в своей внутренней области данный круг, не задан, то для его нахождения выбираем на окружности три некоторые точки, которые обозначаем через А, F и J. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника (по теореме 8.8.2., [4]). Поэтому строим серединный перпендикуляр п к отрезку AF и серединный перпендикуляр р к отрезку FJ. Точку пересечения прямых п и р обозначаем через О. Точка О является искомым центром окружности. Проводим диаметр АЕ. Из точки О восставляем перпендикуляр k к прямой АЕ (порядок построения восставленного к прямой перпендикуляра приведен в [1]). Точки пересечения прямой k с окружностью обозначаем через В и N; отрезок ВN является диаметром окружности. Отрезок ОA является радиусом; обозначим его длину через R (Рис. 1б).

При этом круг разбит на четыре квадранта (Рис. 1б).

2. Деление квадранта на четыре равных сектора.

Строим биссектрису прямого угла АОВ (порядок построения биссектрисы угла приведен в [1]); обозначим точку пересечения биссектрисы с дугой АВ через Р (Рис. 2).
Строим биссектрису угла АОР; обозначим точку пересечения биссектрисы с дугой АР через Е (Рис. 2).
Строим биссектрису угла РОВ; обозначим точку пересечения биссектрисы с дугой РВ через Т (Рис. 2).

Таким образом, прямой угол АОВ разбит на четыре равных угла: АОЕ, ЕОР, РОТ и ТОВ.

3. Разбиение каждого из углов, составляющих одну четверть прямого, на четыре равных угла.

Рассмотрим угол АОЕ. Строим его биссектрису ОА₂; строим биссектрису ОА₁ угла АОА₂; строим биссектрису ОА₃ угла А₂ОЕ (Рис. 3).

Угол АОЕ разбит на четыре равных угла: АОА₁, А₁ОА₂, А₂ОА₃ и А₃ОЕ.

Углы ЕОР, РОТ и ТОВ разбиваются на четыре равных угла таким же способом.

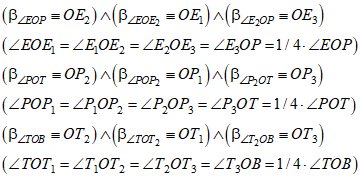
В итоге квадрант АОВ разбит на 16 равных секторов (Рис. 4а).

4. Нахождение в рассматриваемом квадранте длины дуги, равной радиусу окружности.

В квадранте АОВ от точки А нужно вымерить длину дуги, приблизительно равную радиусу данной в задаче окружности. Раствором циркуля последовательно измеряются длины l₀ хорд, соединяющих точки пересечения дуги АВ с лучами, делящими квадрант АОВ на 16 равных секторов (Рис. 4а). Измеренные расстояния последовательно откладываются на отдельно проведенном луче от его начала (Рис. 4б, 5). От начальной точки откладывается расстояние R. Длина дуги, приблизительно равная радиусу окружности, определяется с учетом того, что длины l дуг несколько больше длин l₀ хорд: , где  – средняя длина хорды, стягивающей дугу малого сектора,  – средняя длина дуги, ограничивающей малый сектор.

5. Расчет площади круга.

Площадь круга равна: , где  – площадь квадранта АОВ; площадь квадранта АОВ равна умноженному на 16 усредненному значению площади малого сектора, который будем обозначать через АОА₁. Площадь малого сектора равна [2]: , где  – средняя длина дуги, ограничивающей малый сектор, которая приблизительно равна: . Тогда площадь круга равна:
.
Площадь круга равна: .

6. Построение квадрата, площадь которого равна площади данного круга.

Сторона квадрата, площадь которого равна площади данного круга, равна: . Порядок умножения длины отрезка на корень квадратный в классической геометрии приведен в статье автора [3], в которой изложен порядок построения прямоугольных треугольников, нужных для нахождения искомых длин отрезков.
Сначала строим прямоугольный треугольник АВС с равными катетами длиной R (Рис. 6а).
Порядок построения прямоугольного треугольника следующий: проводим прямую, обозначаем ее через е; выбираем на ней некоторую точку, которую обозначаем через А. Раствором циркуля замеряем расстояние R. Откладываем расстояние R на прямой е от точки А, конец отрезка обозначаем через В.
Из точки В восставляем перпендикуляр к прямой е, который обозначаем через с (Рис. 5.2) (порядок построения восставленного перпендикуляра приведен в статье [1]).

От точки В на прямой с откладываем циркулем расстояние R, конец отрезка обозначаем через С. Соединяем отрезком точки А и С. Образуется треугольник АВС, в котором угол В – прямой и стороны АВ и ВС равны R (Рис. 5.2).
По теореме Пифагора (по теореме 8.3., [4]), которая доказывается в рамках классической геометрии, гипотенуза АС треугольника АВС равна .

Строим прямоугольный треугольник ЕНК, катет НК которого равен R, а катет ЕН равен  (Рис. 6б); для этого замеряется раствором циркуля длина гипотенузы АС построенного перед этим треугольника АВС с равными катетами (Рис. 6а) и откладывается на прямой, на которой лежит сторона ЕН треугольника ЕНК. Порядок построения треугольника ЕНК аналогичен порядку построения треугольника АВС.
По теореме Пифагора, гипотенуза ЕК построенного прямоугольного треугольника ЕНК равна .

Нужно получить геометрически длину, равную . Для этого строим прямоугольный треугольник ОРТ, катет ОР которого равен , а катет РТ равен  (Рис. 6г); для этого замеряется раствором циркуля длина  гипотенузы ЕК построенного перед этим треугольника ЕНК (Рис. 6б) и откладывается на прямой, на которой лежит сторона ОР треугольника ОРТ.
Длина  получается путем разбиения отрезка А₁А₉ длиной R на 8 равных частей и замера расстояния А₁А₄ в 3 части:  (Рис. 6в); порядок разбиения отрезка на восемь равных частей приведен в Приложении к этой статье; в [4] приведен порядок деления отрезка на п равных частей на примере пяти частей (следствие 6.5.9. теоремы 6.5.5.).
По теореме Пифагора, гипотенуза d треугольника ОРТ равна: .

Строим квадрат со стороной, равной:  (Рис. 7); длина стороны квадрата замеряется раствором циркуля по гипотенузе d прямоугольного треугольника ОРТ с катетами, равными  и  (Рис. 6г).
Квадрат строится следующим образом. Проводим прямую, обозначаем ее через р. На прямой р берем некоторую точку, которую обозначаем через А. Из точки А восставляем перпендикуляр к прямой р, обозначим его через АК. Проводим дугу окружности с центром в точке А и радиусом d, точки пересечения дуги с прямой АК и с прямой р обозначаем через В и D соответственно. Расстояния АВ и АD равны d. Из точки D восставляем перпендикуляр к прямой р, обозначим его через DМ. От точки D на прямой DМ откладываем расстояние d, конец отрезка обозначаем через С. Соединяем отрезком точки В и С, при этом образуется четырехугольник АВСD. Прямые АD и ВС – равноудаленные и, следовательно, параллельные (по теореме 3.10. [4]); прямые АВ и DС параллельны как перпендикулярные одной и той же прямой р (по теореме 3.3., [4]), следовательно, четырехугольник АВСD является параллелограммом. По второму свойству параллелограмма (по теореме 6.4.2., [4]), стороны АD и ВС равны, углы ВАD и ВСD, углы АВС и АDС равны, следовательно, четырехугольник АВСD является квадратом.

Площадь квадрата АВСD (Рис. 7) равна площади данного круга: , то есть построенный квадрат представляет собой решение поставленной задачи.

7. Решение обратной задачи – построение круга, площадь которого равна площади данного квадрата.Дано: Квадрат со стороной а_□ некоторой длины b (Рис. 10).
Задача: По правилам классической геометрии построить круг, площадь которого равна площади данного квадрата.
Решение: Из задачи нахождения квадратуры круга следует, что: , следовательно, для нахождения радиуса искомого круга нужно провести деление длины b на корень квадратный: . Геометрическое деление длины отрезка на корень квадратный отлично от алгебраического, так как все рассматриваемые отрезки не коллинеарны.
Порядок деления длины отрезка на корень квадратный подробно изложен в статье автора [3]; здесь он будет приводиться кратко, без доказательств, которые приведены в указанной статье.
Сначала нужно построить прямоугольный треугольник, гипотенуза которого пропорциональна. Для этого берем раствором циркуля некоторое расстояние с. Строим прямоугольный треугольник ОРТ с равными катетами длиной с (Рис. 8а). По теореме Пифагора, его гипотенуза ОТ равна .

Строим прямоугольный треугольник ЕНF с катетами длиной с и  (Рис. 8б); длина  замеряется по гипотенузе ОТ построенного перед этим треугольника ОРТ с равными катетами (Рис. 8а). По теореме Пифагора, гипотенуза EF треугольника ЕНF равна .

Чтобы получить длину , строим прямоугольный треугольник KTM с катетом KT длиной  и катетом TM длиной  (Рис. 8г); длина  замеряется по гипотенузе EF треугольника ЕНF с катетами длиной с и  (Рис. 8б).
Длина  определяется путем разбиения отрезка длиной с на 8 равных частей и замера суммарной длины трех частей (Рис. 8в); порядок разбиения отрезка на 8 равных частей описан в Приложении к этой статье.
По теореме Пифагора, гипотенуза КМ треугольникa КТМ (Рис. 8г) равна .

Строим прямоугольный треугольник, подобный треугольнику КМТ по стороне и двум прилежащим углам, гипотенуза которого равна b. Для этого: проводим прямую р; берем на ней некоторую точку, которую обозначаем через А; откладываем от точки А расстояние b, обозначаем конец отрезка через В (Рис. 9а): .

От прямой р строим угол с вершиной в точке В, равный углу КМТ: проводим дугу окружности с центром в точке М и некоторым радиусом r; точки пересечения этой дуги с отрезками КМ и МТ обозначаем через С и Е соответственно (Рис. 8г). Проводим дугу окружности с центром в точке В и тем же радиусом r; точку пересечения этой дуги с отрезком АВ обозначаем через Р. Замеряем раствором циркуля расстояние СЕ. Проводим дугу окружности с центром в точке Р и радиусом СЕ; точку пересечения этой дуги с предыдущей дугой обозначаем через О. Через точку О проводим луч с началом в точке В (Рис. 9а).

От прямой р в той же полуплоскости строим угол с вершиной в точке А, равный углу МКТ: проводим дугу окружности с центром в точке К и некоторым радиусом R; точки пересечения этой дуги с отрезками КМ и КТ обозначаем через G и F соответственно (Рис. 8г). Проводим дугу окружности с центром в точке А и тем же радиусом R; точку пересечения этой дуги с отрезком АВ обозначаем через J. Замеряем раствором циркуля расстояние GF. Проводим дугу окружности с центром в точке J и радиусом GF; точку пересечения этой дуги с предыдущей дугой обозначаем через Н. Через точку Н проводим луч с началом в точке А (Рис. 9а).

Луч АН пересекается с лучом ВО, точку их пересечения обозначим через С (Рис. 9а). Образуется треугольник АВС, подобный треугольнику КМТ по стороне и двум прилежащим углам (Ах. 8.7.2., [4]) и, следовательно, прямоугольный; его катеты считаем соответственно пропорциональными R. Из определения подобных треугольников (Def. 8.6., [4]) следует, что: , при этом , , , следовательно, .

Нужно геометрически определить длину R. Делим отрезок ВС на три равные части (Рис. 9б); порядок разделения отрезка ВС на три равные части – тот же, что и порядок разбиения отрезка на восемь равных частей (в Приложении). Длина отрезка ВI равна 2/3 длины отрезка ВС. Проводим луч а от некоторой точки, которую обозначим через В; от точки В последовательно откладываем четыре раза расстояние ВI, конечную точку обозначаем через Н (Рис. 9в). Длина отрезка ВН равна искомому радиусу круга (Рис. 9в).

На плоскости выбираем некоторую точку, обозначаем ее через О и проводим окружность с центром в точке О и радиусом R (длиной ВН) (Рис. 10). Площадь круга, ограниченного проведенной окружностью, равна площади заданного квадрата, таким образом, задача решена.

Приложение.

Разбиение отрезка на восемь равных частей.

Нужно разбить отрезок длиной R на восемь равных отрезков. Проведем прямую а, выберем на ней некоторую точку, которую обозначим через А₁. От точки А₁ отложим отрезок длиной R, конец отрезка обозначим через А₉. На произвольном расстоянии от прямой а проводим параллельную ей прямую, обозначаем ее через с; порядок построения параллельной прямой приведен в [4, п. 3.10.2.]. На прямой с берем произвольную точку С₁ (со стороны точки А₁); от нее откладываем циркулем некоторое расстояние l и обозначаем полученную точку через С₂, расстояние С₁С₂ равно l; от точки С₂ откладываем то же самое расстояние l и получаем точку С₃, расстояние С₂С₃ равно l; от точки С₃ откладываем то же самое расстояние l и получаем точку С₄ и так далее; от точки С₈ откладываем то же самое расстояние l и получаем точку С₉, расстояние С₈С₉ равно l. Через точки А₁ и С₁, точки А₉ и С₉ проводим прямые до их пересечения в точке, которую обозначаем через М. Через точки М и С₂, М и С₃ и так далее проводим прямые, точки их пересечения с отрезком А₁А₉ обозначаем через А₁, А₂, …, А₇, А₈ (Рис. 11); эти точки разбивают отрезок А₁А₉ на восемь равных частей.

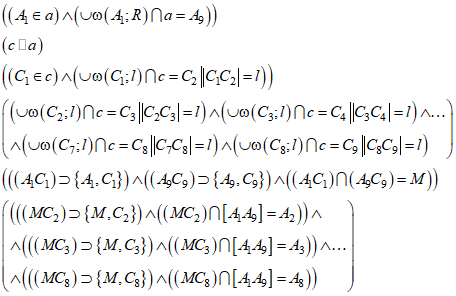
Доказательство: Углы С₁С₃М и А₁А₃М являются соответственными при пересечении секущей МС₃ параллельных прямых а и с и, следовательно, равными (по теореме 6.2.1., [4]). Углы С₁МС₃ и А₁МА₃ равны по аксиоме о независимости величины угла от длины его сторон (Ах. 4.3.2., [4]). Значит, треугольники С₁С₃М и А₁А₃М (Рис. 11) подобны по двум углам (Ах. 8.7.2., [4]); коэффициент подобия k может быть определен отношением: . Из определения подобия (Def. 6.11., [4]) следует, что: , , при этом . Отсюда следует, что: .

Углы С₃С₅М и А₃А₅М являются соответственными при пересечении секущей МС₅ параллельных прямых а и с и, следовательно, равными (по теореме 6.2.1., [4]). Углы С₃МС₅ и А₃МА₅ равны по аксиоме о независимости величины угла от длины его сторон (Ах. 4.3.2., [4]). Значит, треугольники С₃С₅М и А₃А₅М (Рис. 11) подобны по двум углам (Ах. 8.7.2., [4]); коэффициент подобия k₂ может быть определен отношением:
 – в силу подобия треугольников С₁С₃М и А₁А₃М. Из определения подобия (Def. 6.11., [4]) следует, что: , , при этом . Следовательно: . Так как , то, по определению подобия (Def. 6.11.): .

Углы С₅С₇М и А₅А₇М являются соответственными при пересечении секущей МС₇ параллельных прямых а и с и, следовательно, равными (по теореме 6.2.1., [4]). Углы С₅МС₇ и А₅МА₇ равны по аксиоме о независимости величины угла от длины его сторон (Ах. 4.3.2., [4]). Значит, треугольники С₅С₇М и А₅А₇М (Рис. 11) подобны по двум углам (Ах. 8.7.2., [4]); коэффициент подобия k₃ может быть определен отношением:  – в силу подобия треугольников С₃С₅М и А₃А₅М. Из определения подобия (Def. 6.11., [4]) следует, что: , , при этом . Следовательно: . Так как , то, по определению подобия (Def. 6.11.): .

Углы С₇С₉М и А₇А₉М являются соответственными при пересечении секущей МС₉ параллельных прямых а и с и, следовательно, равными (по теореме 6.2.1., [4]). Углы С₇МС₉ и А₇МА₉ равны по аксиоме о независимости величины угла от длины его сторон (Ах. 4.3.2., [4]). Значит, треугольники С₇С₉М и А₇А₉М (Рис. 11) подобны по двум углам (Ах. 8.7.2., [4]); коэффициент подобия k₄ может быть определен отношением:  – в силу подобия треугольников С₅С₇М и А₅А₇М. Из определения подобия (Def. 6.11., [4]) следует, что: , , при этом . Следовательно: . Так как , то, по определению подобия (Def. 6.11.): .

Выводы. В рамках классической геометрии найдена квадратура круга с наибольшей точностью, то есть с помощью простой линейки и циркуля построен квадрат, площадь которого равна площади данного круга. Наиболее точно решена и обратная задача, являющаяся более сложной, – с помощью простой линейки и циркуля построен круг, площадь которого равна площади данного квадрата.

1. Плисова Н.Н. Нахождение квадратуры круга в классической геометрии и решение обратной задачи // Современные научные исследования и инновации, 2022, № 10 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2022/10/98924
2. Выгодский М.Я. Справочник по элементарной математике. – М.: АСТ: Астрель, 2006. – 509 с.
3. Плисова Н.Н. Умножение и деление длины отрезка на корни квадратные в классической геометрии // Современные научные исследования и инновации. 2022, № 10 [Электронный ресурс]. URL:  https://web.snauka.ru/issues/2022/10/98923
4. Плисова Н.Н. Основания геометрии. – 5-е изд. – М.: Эдитус, 2023. – 284 с.

Все статьи автора «Плисова Ника Николаевна»