Задача построения по правилам классической геометрии отрезка, длина которого равна длине заданного геометрически отрезка, умноженной или деленной на корень квадратный из некоторого целого числа, представляет тем больший теоретический интерес, что в классической геометрии расстояния или длины отрезков не имеют числового выражения, а корни квадратные выражаются иррациональными числами.
В классической геометрии все построения выполняются простой линейкой, не имеющей шкалы, и циркулем. Расстояния измеряются раствором циркуля. Углы непосредственно не измеряются (транспортир не применяется).
Доказательство базируется на аксиоматике планиметрии, которая приведена в книге автора [1] и не приводится заново в этой статье.
Дано: расстояние а, заданное геометрически (Рис. 2).
1. Умножение длины отрезка на корень квадратный из двух.
Задача: построить по правилам классической геометрии отрезок, длина которого равна длине а исходного отрезка, умноженной на корень квадратный из двух.
Сначала строим прямоугольный треугольник с равными катетами длиной а, заданной геометрически.
Для этого: проводим прямую, обозначаем ее через е; выбираем на ней некоторую точку, которую обозначаем через А. Раствором циркуля замеряем расстояние а. Откладываем расстояние а на прямой е от точки А, конец отрезка обозначаем через В.
Из точки В восставляем перпендикуляр к прямой е. Перпендикуляр восставляется следующим способом: проводим дуги окружности с центром в точке В и некоторым радиусом r, точки пересечения дуг с прямой е обозначаем через К и М (Рис. 1); проводим дугу окружности с центром в точке К и радиусом КМ; проводим дугу окружности с центром в точке М и радиусом МК=КМ; точку пересечения дуг обозначаем через Р. Через точки В и Р проводим прямую; прямая ВР перпендикулярна прямой е (Рис. 1).
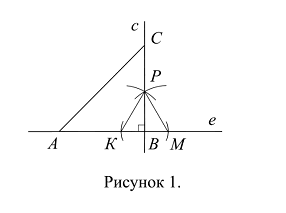
Нужно доказать, что прямая ВР перпендикулярна прямой е. Радиусы окружности с центром в точке К и окружности с центром в точке М равны: КР=МР, при том что ВК=ВМ. ![]() по трем сторонам (Ax. 8.5.3.), следовательно,
по трем сторонам (Ax. 8.5.3.), следовательно, ![]() по аксиоме о равенстве фигур (Ax. 6.8.). Эти углы – смежные, то есть:
по аксиоме о равенстве фигур (Ax. 6.8.). Эти углы – смежные, то есть: ![]() (Def. 4.14.), следовательно,
(Def. 4.14.), следовательно, ![]() , то есть эти углы являются прямыми (Def. 4.10.). Перпендикулярность прямых ВР и е доказана (Def. 2.10.).
, то есть эти углы являются прямыми (Def. 4.10.). Перпендикулярность прямых ВР и е доказана (Def. 2.10.).
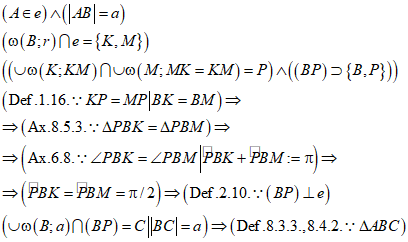
От точки В на прямой ВР откладываем циркулем расстояние а, конец отрезка обозначаем через С. Соединяем отрезком точки А и С. Образуется треугольник АВС, в котором угол В – прямой и стороны АВ и ВС равны (Рис. 2).
По теореме Пифагора (теореме 9.3.), которая доказывается в рамках классической геометрии [1, п. 9.3.], гипотенуза этого треугольника равна: ![]() .
.
Гипотенуза прямоугольного треугольника с равными катетами длиной а равна ![]() и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из двух.
и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из двух.
2. Умножение длины отрезка на корень квадратный из трех.
Задача: построить по правилам классической геометрии отрезок, длина которого равна длине а исходного отрезка, умноженной на корень квадратный из трех.
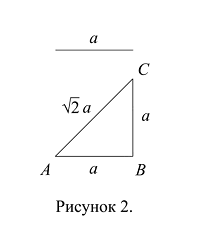
Строим прямоугольный треугольник с катетами, равными а и ![]() (Рис. 3); порядок построения этого треугольника – тот же, что и порядок построения прямоугольного треугольника с равными катетами (п. 1. этой статьи), только от точки А на прямой е откладывается расстояние
(Рис. 3); порядок построения этого треугольника – тот же, что и порядок построения прямоугольного треугольника с равными катетами (п. 1. этой статьи), только от точки А на прямой е откладывается расстояние ![]() (а не а), от точки В на прямой ВР откладывается расстояние а. Расстояние
(а не а), от точки В на прямой ВР откладывается расстояние а. Расстояние ![]() замеряется по длине гипотенузы прямоугольного треугольника с равными катетами (Рис. 2).
замеряется по длине гипотенузы прямоугольного треугольника с равными катетами (Рис. 2).
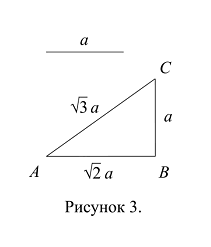
По теореме Пифагора (теореме 9.3.), гипотенуза прямоугольного треугольника с катетами длиной а и ![]() равна:
равна: ![]() .
.
Гипотенуза прямоугольного треугольника с катетами длиной а и ![]() равна
равна ![]() и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из трех.
и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из трех.
3. Умножение длины отрезка на корень квадратный из четырех.
Задача: построить по правилам классической геометрии отрезок, длина которого равна длине а исходного отрезка, умноженной на корень квадратный из четырех.
Вместо простого умножения исходной длины на два проводим то же построение, что и в предыдущем случае, чтобы сохранить общую схему построений и данное звено в ней. Строим прямоугольный треугольник с катетами длиной а и ![]() (Рис. 4); порядок построения этого треугольника – тот же, что и порядок построения прямоугольного треугольника с катетами длиной а и
(Рис. 4); порядок построения этого треугольника – тот же, что и порядок построения прямоугольного треугольника с катетами длиной а и ![]() , только от точки А на прямой е откладывается расстояние
, только от точки А на прямой е откладывается расстояние ![]() (а не
(а не ![]() ), от точки В на прямой ВР откладывается расстояние а. Расстояние
), от точки В на прямой ВР откладывается расстояние а. Расстояние ![]() замеряется по длине гипотенузы прямоугольного треугольника с катетами а и
замеряется по длине гипотенузы прямоугольного треугольника с катетами а и ![]() (Рис. 3).
(Рис. 3).
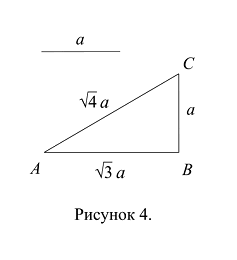
По теореме Пифагора (теореме 9.3.), гипотенуза прямоугольного треугольника с катетами длиной а и ![]() равна:
равна: ![]() .
.
Гипотенуза прямоугольного треугольника с катетами длиной а и ![]() равна
равна ![]() и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из четырех.
и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из четырех.
4. Умножение длины отрезка на корень квадратный из пяти.
Задача: построить по правилам классической геометрии отрезок, длина которого равна длине а исходного отрезка, умноженной на корень квадратный из пяти.
Строим прямоугольный треугольник с катетами длиной а и ![]() (Рис. 5); порядок построения этого треугольника – тот же, что и порядок построения прямоугольного треугольника с катетами длиной а и
(Рис. 5); порядок построения этого треугольника – тот же, что и порядок построения прямоугольного треугольника с катетами длиной а и![]() , только от точки А на прямой е откладывается расстояние
, только от точки А на прямой е откладывается расстояние ![]() (а не
(а не ![]() ), от точки В на прямой ВР откладывается расстояние а. Расстояние
), от точки В на прямой ВР откладывается расстояние а. Расстояние ![]() замеряется по длине гипотенузы прямоугольного треугольника с катетами длиной а и
замеряется по длине гипотенузы прямоугольного треугольника с катетами длиной а и ![]() (Рис. 4) (или же простым умножением на два).
(Рис. 4) (или же простым умножением на два).
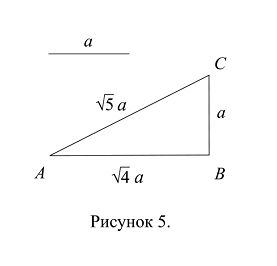
По теореме Пифагора (теореме 9.3.), гипотенуза прямоугольного треугольника с катетами длиной а и ![]() равна:
равна: ![]() .
.
Гипотенуза прямоугольного треугольника с катетами длиной а и ![]() равна
равна ![]() и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из пяти.
и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине а данного отрезка, умноженной на корень квадратный из пяти.
Этим же способом может быть осуществлено геометрически умножение длины а данного отрезка на корень квадратный из чисел, бoльших пяти.
5. Деление длины отрезка на корень квадратный из двух.
Дано: отрезок длиной b (задан геометрически).
Задача: построить по правилам классической геометрии отрезок, длина а которого равна длине b данного отрезка, деленной на корень квадратный из двух: ![]() .
.
Из п. 1. этой статьи следует, что гипотенуза прямоугольного треугольника с равными катетами длиной а равна ![]() . Нужно построить прямоугольный треугольник, гипотенуза которого равна
. Нужно построить прямоугольный треугольник, гипотенуза которого равна ![]() , при этом его катеты будут равны а, то есть катет даст искомую длину.
, при этом его катеты будут равны а, то есть катет даст искомую длину.
Проводим прямую р; берем на ней некоторую точку и обозначаем ее через А. От точки А на прямой р откладываем расстояние b, точку пересечения обозначаем через В. Из точки А восставляем перпендикуляр к прямой р, который обозначаем через п; из точки В восставляем перпендикуляр к прямой р, который обозначаем через с (Рис. 6); порядок построения восставленного перпендикуляра приведен в п. 1. этой статьи.
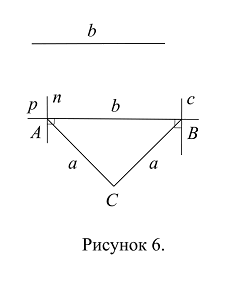
Строим биссектрису угла между прямой р и прямой п с вершиной в точке А и биссектрису угла между прямой р и прямой с с вершиной в точке В. Биссектриса угла (рп) строится следующим образом: проводим дугу окружности с центром в точке А и некоторым радиусом r1, точку пересечения дуги с прямой р обозначаем через К, точку пересечения дуги с прямой п обозначаем через М (Рис. 7); проводим дугу окружности с центром в точке К и радиусом КА; проводим дугу окружности с центром в точке М и радиусом МА=КА; точку пересечения дуг обозначаем через Р. Через точки А и Р проводим прямую; прямая АР является биссектрисой угла (рп) (Рис. 7).
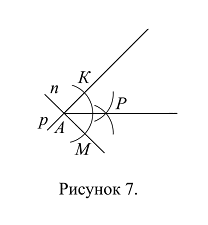
Действительно, так как радиусы окружностей равны (Def. 1.16.), треугольник АКР равен треугольнику АМР по трем сторонам (Ax. 8.5.3.), следовательно, угол КАР равен углу МАР по аксиоме о равенстве фигур (Ax. 6.8.), следовательно, луч АР является биссектрисой угла КАМ (Def. 8.9.3.), то есть биссектрисой угла (рп) (по аксиоме 4.3.2.).
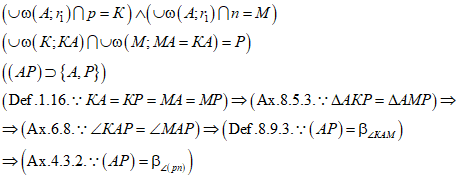
Биссектриса угла (рс) строится таким же образом. Точку пересечения биссектрис обозначаем через С (Рис. 6).
По аксиоме 8.8. о свойствах треугольника, треугольник АВС является равнобедренным и, по теореме 5.4. о сумме углов в треугольнике, прямоугольным. Гипотенуза АВ равна b, следовательно, по теореме Пифагора (по теореме 9.3.), длина а равна ![]() и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине b данного отрезка, деленной на корень квадратный из двух.
и является искомым результатом построения по правилам классической геометрии отрезка, длина которого равна длине b данного отрезка, деленной на корень квадратный из двух.
.gif)
6. Деление длины отрезка на корень квадратный из трех.
Дано: отрезок длиной b (задан геометрически).
Задача: построить по правилам классической геометрии отрезок, длина а которого равна длине b данного отрезка, деленной на корень квадратный из трех: ![]() .
.
Согласно п. 2. этой статьи, гипотенуза прямоугольного треугольника с катетами длиной а и ![]() равна
равна ![]() . Нужно построить прямоугольный треугольник, гипотенуза которого равна
. Нужно построить прямоугольный треугольник, гипотенуза которого равна ![]() , при этом его катеты будут равны а и
, при этом его катеты будут равны а и ![]() , то есть меньший катет даст искомую длину. Это задача, обратная задаче построения прямоугольного треугольника по катетам а и
, то есть меньший катет даст искомую длину. Это задача, обратная задаче построения прямоугольного треугольника по катетам а и ![]() .
.
Берем раствором циркуля некоторое расстояние с. Строим прямоугольный треугольник с равными катетами длиной с; порядок построения такого треугольника описан в п. 1. этой статьи. По теореме Пифагора (по теореме 9.3.), его гипотенуза равна ![]() (Рис. 8).
(Рис. 8).
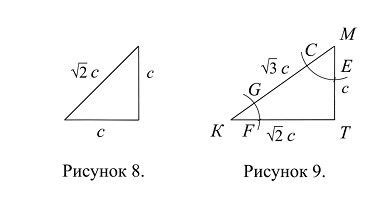
Строим прямоугольный треугольник с катетами длиной с и ![]() ; по теореме Пифагора (по теореме 9.3.), его гипотенуза равна
; по теореме Пифагора (по теореме 9.3.), его гипотенуза равна ![]() (Рис. 9); порядок построения прямоугольного треугольника с такими катетами описан в п. 2. этой статьи. Обозначим построенный треугольник через КМТ (Рис. 9).
(Рис. 9); порядок построения прямоугольного треугольника с такими катетами описан в п. 2. этой статьи. Обозначим построенный треугольник через КМТ (Рис. 9).
Строим прямоугольный треугольник, подобный треугольнику КМТ по стороне и двум прилежащим углам. Для этого: проводим прямую р; берем на ней некоторую точку, которую обозначаем через А; откладываем от точки А расстояние b, обозначаем конец отрезка через В (Рис. 10): ![]() .
.
От прямой р строим угол с вершиной в точке В, равный углу КМТ (Рис. 9): проводим дугу окружности с центром в точке М и некоторым радиусом r; точки пересечения этой дуги с отрезками КМ и МТ обозначаем через С и Е соответственно. Проводим дугу окружности с центром в точке В и тем же радиусом r; точку пересечения этой дуги с отрезком АВ обозначаем через Р. Замеряем раствором циркуля расстояние СЕ. Проводим дугу окружности с центром в точке Р и радиусом СЕ; точку пересечения этой дуги с предыдущей дугой обозначаем через О. Через точку О проводим луч с началом в точке В (Рис. 10).
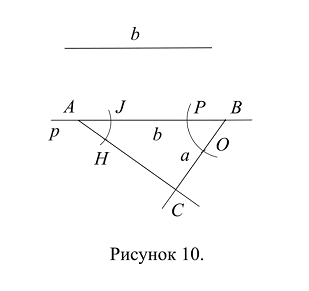
Треугольник РВО равен треугольнику СМЕ по трем сторонам (Ах. 8.5.3.), следовательно, угол РВО равен углу СМЕ по аксиоме о равенстве фигур (Ах. 6.8.); по аксиоме 4.3.2. о независимости величины угла от длины его сторон, угол РВО равен углу КМТ.
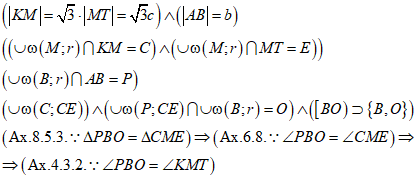
От прямой р строим угол с вершиной в точке А, равный углу МКТ (Рис. 9): проводим дугу окружности с центром в точке К и некоторым радиусом R; точки пересечения этой дуги с отрезками КМ и КТ обозначаем через G и F соответственно. Проводим дугу окружности с центром в точке А и тем же радиусом R; точку пересечения этой дуги с отрезком АВ обозначаем через J. Замеряем раствором циркуля расстояние GF. Проводим дугу окружности с центром в точке J и радиусом GF; точку пересечения этой дуги с предыдущей дугой обозначаем через Н. Через точку Н проводим луч с началом в точке А (Рис. 10).
Треугольник JAH равен треугольнику GKF по трем сторонам (Ах. 8.5.3.), следовательно, угол JAH равен углу GKF по аксиоме о равенстве фигур (Ах. 6.8.); по аксиоме 4.3.2. о независимости величины угла от длины его сторон, угол JAH равен углу МKТ.
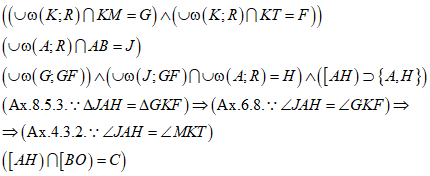
Луч АН пересекается с лучом ВО, точку их пересечения обозначим через С (Рис. 10). Образуется треугольник АВС, подобный треугольнику КМТ по стороне и двум прилежащим углам (Ах. 8.7.2.) и, следовательно, прямоугольный. Из определения подобных треугольников (Def. 8.6.) следует, что: ![]() , при этом
, при этом ![]() , следовательно,
, следовательно, ![]() , значит,
, значит, ![]() , то есть длина отрезка ВС является искомой.
, то есть длина отрезка ВС является искомой.
.gif)
Деление длины заданного отрезка на корни из бoльших чисел проводится этим же способом, то есть сначала строится прямоугольный треугольник с одним катетом произвольной длины и вторым катетом в соответствующей пропорции, а затем строится прямоугольный треугольник, подобный построенному треугольнику, гипотенуза которого равна заданному отрезку. Из подобия треугольников следует пропорциональность их сторон; меньший катет треугольника, гипотенуза которого равна заданной длине, даст искомую длину.
Выводы. Решена, причем точно, задача построения по правилам классической геометрии отрезка, длина которого равна длине заданного геометрически отрезка, умноженной или деленной на корень квадратный из некоторого целого числа. На принципе умножения длины отрезка на корень квадратный путем геометрического построения отрезка искомой длины основана, например, система древнерусских саженей, представляющая собой систему пропорций.
Библиографический список
- Плисова Н.Н. Основания геометрии. – 4-е изд. – М.: Эдитус, 2022. – 224 с.
- Выгодский М.Я. Справочник по элементарной математике. – М.: АСТ: Астрель, 2006. – 509 с.
