ВЕРОЯТНОСТНЫЕ ПОКАЗАТЕЛИ СПОСОБНОСТИ К ОБУЧЕНИЮ ДЛЯ РАЗЛИЧНЫХ РЕЖИМОВ РАБОТЫ АВИАЦИОННОГО ОПЕРАТОРА

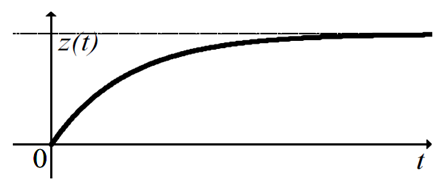
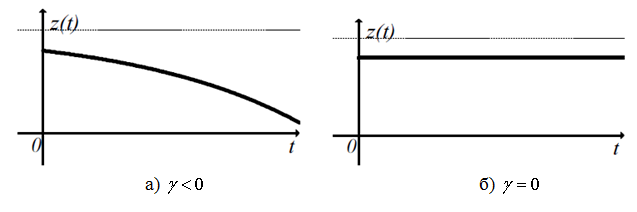Введение Как известно из предыдущих исследований [1], [2], в идеальном случае кривая, описывающая количество освоенных знаний, умений и навыков (ЗУН), со временем приобретает экспоненциальную природу (рис. 1).

Рис. 1 – Идеальная кривая обучения

В начале процесса обучения или тренировки за единицу учебного времени авиационный оператор овладевает большое количество ЗУН. Чем больше сплошная количества затраченного учебного времени – тем меньше ЗУН будет освоено авиационным оператором за единицу учебного времени. В общем случае этот процесс описывается формулой

где  – время обучения, - показатель обучаемости  – показатель начальной обученности  – показатель конечной (желаемой) обучаемости,  – константа, определяющая скорость обучения.

При  происходит процесс обучения, при  процесс обучения приобретает негативной динамики и превращается в процесс забывания (рис. 2а), при уровень ЗУН сохраняется постоянным (рис. 2б).

Рис. 2 Показатель процесса обучения при  и 

В отличие от теории, в реальном процессе обучения всегда непредсказуема часть показателя обучаемости, обусловленная личными свойствами авиационного оператора, его опытом, его эмоциональным состоянием и другими параметрами, которые можно отнести к эргономичности [3].

Таким образом, хотя общий вид функции, описывающей изменение показателя обучаемости для каждого авиационного оператора, будет единственным, каждая частичная ее реализация будет отличаться.

Такие данные лучше описываются стохастическими стационарными моделями с постоянным средним значением [4-6].

Актуальность и постановка задачи Моделирование процесса обучения, тренировки, освоения и воспроизводства ЗУН проводились многими способами и достаточно изучено. Однако, несмотря на наличие стохастических методов моделирования [7], [8], в них не проводится глубокий анализ составляющих элементов показателя обучаемости. Как результат, не различаются чисто стохастические и детерминированные составляющие показателя обучаемости, не проводится их анализ, который позволит распределить авиационных операторов по составляющим их показателей обученности на группы и разработать рекомендации по планированию процесса обучения для групп и каждого авиационного оператора отдельно, улучшая эффективность этого процесса с течением времени и накоплением статистических данных. Этот вопрос всегда актуален, поскольку технически тренажеры и системы обучения постоянно меняются, требующих методологических и алгоритмических разработок.

Таким образом обнаружения указанных составляющих, их математическое описание и анализ и является целью данной статьи.

Результаты исследований Как известно, показатели стационарного стохастического процесса можно представить в виде

где - показатель процесса, - постоянный средний уровень, - случайное отклонение процесса в настоящее время . В идеальном случае при  имеем

Если принять, что функция  соответствует идеальной возрастающей экспоненте из рис. 1, то можно ввести нормированный показатель процесса  . Тогда стационарный стохастический процесс относительно приобретения знаний с нормированным показателем приобретает вид

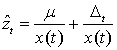
Известно, что  является неизменным средним уровнем стохастического процесса. Для чисто детерминированного процесса без случайной составляющей нормированный средний уровень  . Тогда показатель нормированного стационарного стохастического процесса равна.

то есть описывает стационарный стохастический процесс относительно среднего уровня 1.  В случае считается, что авиационный оператор демонстрирует уровень овладения навыками, что описывается идеальным показательному закону. В реальном тренировке все авиационные операторы обладают личными качествами, которые вносят изменения в значения  . Эти черты аккумулируются в случайное отклонение процесса и сами по себе могут бить разделены на две составляющие  . Первая составляющая – это показатель постоянных личных свойств (ПЛС) авиационных операторов, вторая составляющая – это действительно отклонения случайной величины.

Показатель нормированного стационарного стохастического процесса в таком случае принимает вид

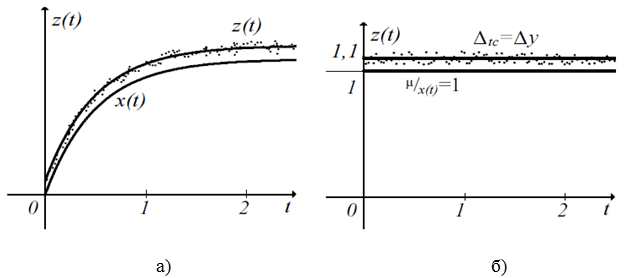
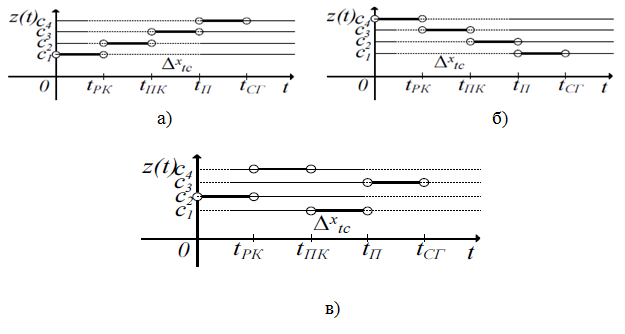
Графически три составляющие графиков нормированного и ненормированного показателей процесса обучения показано на рис. 3 (за базовую функцию взята экспонента).

Рис. 3 – Графики показателей процесса обучения: а) ненормированный, б) нормированный

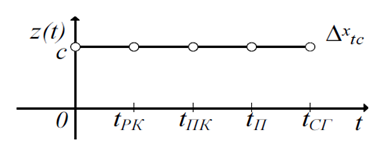
На графиках линиями показано детерминированные составляющие показателя процесса обучения и , а точками показано реальные значения  Как следует из данных  в процессе профессиональной подготовки и деятельности авиационных операторов последовательно проходят четыре стадии, показанные на рис. 4.

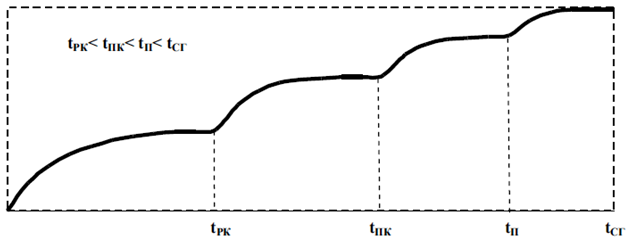Рис. 4 – Трансформация профессиональных ЗУН в процессе тренировок:  - время, необходимое для достижения уровня работы в режиме компенсации;  – преследование с компенсацией;  – оптимальный предсказатель; - предсказание

Согласно модели, представленной на рис. 4, для каждого этапа функция показателя стационарного стохастического процесса может отличаться. Обозначим показатели четырех режимов как  , а соответствующие нормированные показатели как 

где - текущий момент времени. Каждый из нормируемых показателей в свою очередь делится на три составляющие. Обозначим показатели (ПЛС) авиационных операторов как , а настоящие отклонения случайной величины как  .  принимает вид

Функция  остается одинаковой для всех трех режимов при предположении идеальной экспоненты как базовой функции для всех режимов. Учитывая, что различные режимы могут иметь различные базовые функции, обозначим их как  . Тогда  принимает вид

Соответствующие приложения  равны единице в каждом случае, поскольку значение  остаются детерминированными для каждого режима работы авиационного оператора.

Для отдельного авиационного оператора изменение режима в работе может иметь различные последствия с точки зрения его эффективности. Проведение анализа таких изменений лучше всего выполнять, опираясь на детерминированы составляющие показателя нормированного стационарного стохастического процесса. Одна из детерминированных составляющих – это совокупность функций  , которые непосредственно равны постоянном среднему уровню , но их использование позволит только определить, по каким именно идеальным законом воспроизводятся ненормированные кривые показателя процесса обучения в каждом режиме. Другая детерминирована составляющая – это , показатель ПЛС авиационного оператора, который изменяется в соответствии реагируя на особенности работы авиационного оператора.

Рассмотрим переход от режима компенсации к режиму преследования с компенсацией. Этот переход характеризуется изменением данных, предоставляемых авиационным операторам. Если в первом режиме он получал только отклонения контролируемой величины  , то уже во втором режиме он работает с двумя дополнительными параметрами , такими как,  . Итак информационная нагрузка растет, что может привести как к изменению базовой функции обучения, так и к изменению показателя личных свойств. Дальнейший переход к режимам оптимального предсказания и предсказание также увеличивает количество информации, полученной авиационным оператором. Причем, начиная с режима оптимального предсказания, полученная информация осложняется не только количественно, но и качественно. При переходе к третьему режиму она начинает частично приобретать вероятностных характеристики, а при переходе к четвертому режиму в состав имеющейся информации вводятся правила, которые нельзя напрямую вывести из наблюдений за контролируемой величиной.

Рассмотрим случай, когда базовая функция остается постоянной, а показатели личных свойств могут меняться. Для удобства отбросим действительное отклонение случайной величины и обозначим 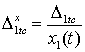 . Тогда необходимо сравнить четыре параметра 

Рассмотрим простейший случай, когда  Очевидно, что в таком случае авиационный оператор демонстрирует одинаковые личные свойства в каждом режиме. Как результат, такой авиационный оператор считается стабильным, и в зависимости от значения c определяется его способность к обучению. В случае авиационный оператор обладает повышенной способностью, в случае авиационный оператор имеет сниженную способность. Графически описан случай представлено на рис. 5.

Рис. 5 – График сравнения показателя ПЛС стабильного авиационного оператора для различных режимов

В усложненном случае с изменением констант соответствуют выражение В данном случае авиационный оператор демонстрирует различные личные свойства в каждом режиме. Способность такого авиационного оператора к обучению нестабильна и дальнейшие выводы зависят от значений  . Если , то авиационный оператор нестабильно улучшает результаты. Если , то авиационный оператор  нестабильно ухудшает результаты. В любом другом случае дополнительные выводы зависят от детального анализа его результатов. Графически описан случай представлен на рис. 6.

Рис. 6 – Сравнение показателей ПЛС нестабильного авиационного оператора для различных режимов: а) нестабильное улучшения; б) нестабильное ухудшения; в) нестабильная неопределенность

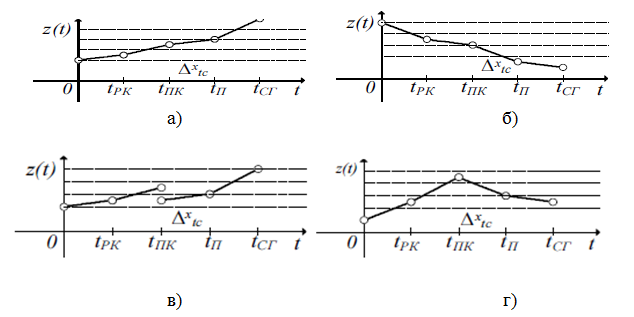
 Следующее усложнение модели – изменение установившегося значения на линейную функцию  . Тогда . При наличии линейной функции когнитивные свойства авиационного оператора меняются с течением времени в пределах каждого охваченного режима. Способность такого авиационного оператора к обучению нестабильна и дальнейшие выводы зависят от динамики

Если  , и одновременно, то авиационный оператор постоянно улучшает результаты. Напротив при и одновременно , то авиационный оператор постоянно ухудшает результаты. Если и одновременно, то имеет место точка резкого падения демонстрируемого уровня ПЛС авиационного оператора при переходе к новому режиму с последующим ростом. Если такое, что , то присутствует точка изменения динамики демонстрируемого уровня ПЛС авиационного оператора, до которой его показатели росли, а после которой его показатели начали спадать. Графически описан случай представлен на рис. 7.

Рис. 7 – Сравнение показателей ПЛС авиационного оператора для различных режимов с линейным законом их изменения: а) постоянное улучшение; б) постоянное ухудшение; в) с точкой временного ухудшения; г) с точкой постоянного ухудшения

Замена линейных функций на нелинейные принципиально не повлияет на графическое описание модели. Каждый граф можно будет разбить на составляющие типа точек разрывов, перегиба и постоянного роста или промежутков падения.

Опираясь на динамику ПЛС авиационного оператора, можно отработать рекомендации, по программе их тренировок. Например, для модели с рис. 5, 6а, 7а и 7в рекомендовать оставить учебную программу без изменений; для рис. 6б и 7б рекомендуется уменьшить темп и увеличить количество времени для освоения ЗУН; для рис. 6в и 7г рекомендуется выделить те режимы, в которых авиационный оператор демонстрировал худшие результаты, и уделить больше внимания тем задачам, которые авиационный оператор должен выполнять в этих режимах. Типовые рекомендации для каждого авиационного оператора также могут учитывать – какие именно ЗУН он овладел во время работы в каждом из режимов, как связаны между собой освоены ЗУН, какой была форма базовой функции обучения и тому подобное.

Выводы. Согласно полученным результатам (график показателей постоянных личных свойств стабильного авиационного оператора, график показателей постоянных личных свойств нестабильного авиационного оператора, график показателей переменных личных свойств авиационного оператора), которые впервые формально описывают составляющие показателя обучаемости для четырех режимов работы авиационного оператора, можно утверждать, что авиационный оператор с различными показателями динамики ПЛС должен получать откорректированы учебные программы. Обычно изменение учебных программ осложняется ограниченным временем, предназначенным для освоения включенных в программу ЗУН, но даже к случае невозможности внесения изменений в саму программу, ряд авиационных операторов может быть допущенной к дальнейшей учебе или работы с учетом особенностей их динамики ПЛС различных режимах.

1. Акофф Р., Эмери Ф. О целеустремленных системах. М.: Сов. радио, 1974. – 272 с
2. Введение в эргономику, М., 1974; 3инченко В. П., Мунипов В. М., Смолян Г. Л., Эргономические основы организации труда, М., 1974
3. Ильин О .И. Эргономика : учеб. пособие / О .И . Ильин, В .Н . Сидорова. –  М . : Рос. эк. акад. им. Г .В . Плеханова. 2001. – 154 с
4. Антонова Г.М. Методика ЛП-поиска с усреднением для исследования динамических стохастических процессов или систем, представленных имитационными моделями // Препринт, Институт проблем управления им. В.А. Трапезникова РАН, Москва, 2000, 74 с.
5. W.A.Fuller    Introduction to Statistical Time Series. – 2nd ed., N.Y., Wiley, 1996
6. Вильсон А.Дж. Энтропийные методы моделирования сложных систем. М.: Наука, 1978
7. Аткинсон Р., Бауэр Г., Кротерс З. Введение в математическую теорию обучения: Пер. с англ. – М.: Мир, 1969. – 486 с
8. Игнатьев М. Б. Мир как модель внутри сверхмашины и виртуальные миры // Искусственный интеллект: междисциплинарный подход. Под ред. Д.И. Дубровского и В.А. Лекторского – М.: ИИнтеЛЛ, 2006. – С. 264-275.
9. Авиационные цифровые системы контроля и управления. / Под редакцией В.А. Мясникова и В.П. Петрова. Л: Машиностроение, Ленингр. отд., 1976.

Все статьи автора «Бадекин Максим Юрьевич»