В классической геометрии все построения выполняются простой линейкой, не имеющей шкалы, и циркулем; расстояния измеряются раствором циркуля.
Вывод равенства построенных углов основывается на аксиоматике планиметрии, которая приведена в книге автора [1] и не приводится заново в этой статье.
Способ точного деления угла и дуги окружности на три равные части по правилам классической геометрии.
Дано: угол произвольной величины, заданный геометрически.
Задача: с помощью простой линейки и циркуля разделить данный угол на три равные части.
Решение: Пускай угол с вершиной в точке О образован лучами а и с. Проводим дугу окружности с центром в точке О и некоторым радиусом R; точки ее пересечения с лучами а и с, являющимися сторонами данного угла, обозначаем через А и С соответственно (Рис. 1).
Проводим дугу окружности с центром в точке О и радиусом 2R; точку ее пересечения с лучом а обозначаем через В (до луча с эту дугу не доводим). Соотношение между радиусами второй и первой окружностей может быть и другим; удвоение радиуса наиболее просто и удобно, для чего на луче а от точки А откладывается расстояние R, конец отрезка обозначается через В. На дуге окружности с центром в точке О и радиусом 2R от точки В последовательно откладываем три раза некоторое расстояние п: раствором циркуля последовательно откладываются хорды длиной п, не достигая луча с; концы отложенных отрезков обозначаются через В1, В2 и В3 (Рис. 1). По теореме 5.2.4., длины дуг ВВ1, В1В2 и В2В3, которые стягивают равные хорды ВВ1, В1В2 и В2В3, равны.
Через точки С и В3 проводим прямую; луч а продолжаем по прямой до пересечения его с прямой СВ3, точку пересечения обозначаем через Р. Проводим прямую через точки Р и В1, точку ее пересечения с дугой АС обозначаем через А1; проводим прямую через точки Р и В2, точку ее пересечения с дугой АС обозначаем через А2 (Рис. 1).
Через точку А1 проводим луч с началом в точке О; через точку А2 проводим луч с началом в точке О. Лучи ОА1 и ОА2 разбивают угол АОС на три равные части (Рис. 1).


Действительно, хорды ВВ1, В1В2, В2В3 равны: ![]() , следовательно, по теореме 5.2.4. (доказанной в п. 2. этой статьи), длины соответствующих дуг тоже равны:
, следовательно, по теореме 5.2.4. (доказанной в п. 2. этой статьи), длины соответствующих дуг тоже равны: ![]() .
.
Окружности с центром в точке О и радиусами R и k·R являются концентрическими (Def. 5.15.1.), где ![]() ; дуги ВВ3 и АС параллельны по определению параллельных кривых, данному в [3]. По аксиоме 4.3.2. о независимости величины угла от длины его сторон, угол АРА1 равен углу ВРВ1, угол А1РА2 равен углу В1РВ2, угол А2РС равен углу В2РВ3 (Рис. 1):
; дуги ВВ3 и АС параллельны по определению параллельных кривых, данному в [3]. По аксиоме 4.3.2. о независимости величины угла от длины его сторон, угол АРА1 равен углу ВРВ1, угол А1РА2 равен углу В1РВ2, угол А2РС равен углу В2РВ3 (Рис. 1): ![]() ,
, ![]() ,
, ![]() , при этом длины дуг ВВ1, В1В2, В2В3, ограниченных сторонами углов ВРВ1, В1РВ2, В2РВ3, равны:
, при этом длины дуг ВВ1, В1В2, В2В3, ограниченных сторонами углов ВРВ1, В1РВ2, В2РВ3, равны: ![]() , следовательно, длины дуг АА1, А1А2 и А2С, ограниченных сторонами углов АРА1, А1РА2 и А2РС, тоже равны по аксиоме 6.7. о равенстве фигур:
, следовательно, длины дуг АА1, А1А2 и А2С, ограниченных сторонами углов АРА1, А1РА2 и А2РС, тоже равны по аксиоме 6.7. о равенстве фигур: ![]() . Значит, дуга АС разбита на три равные части (Рис. 1); таким образом решена задача разделения дуги окружности на три равные части.
. Значит, дуга АС разбита на три равные части (Рис. 1); таким образом решена задача разделения дуги окружности на три равные части.
Длина дуги окружности равна произведению радиуса окружности на угловую величину дуги, выраженную в радианах [2]: ![]() ,
, ![]() ,
, ![]() ; угловая величина дуги равна величине центрального угла, стороны которого ограничивают эту дугу. Из равенства длин дуг АА1, А1А2 и А2С следует равенство их угловых величин:
; угловая величина дуги равна величине центрального угла, стороны которого ограничивают эту дугу. Из равенства длин дуг АА1, А1А2 и А2С следует равенство их угловых величин: ![]() . Равенство угловых величин дуг АА1, А1А2 и А2С означает равенство соответствующих им центральных углов (Рис. 1):
. Равенство угловых величин дуг АА1, А1А2 и А2С означает равенство соответствующих им центральных углов (Рис. 1): ![]() ; величина каждого из них равна 1/3 величины угла АОС (по аксиоме 4.7.1.).
; величина каждого из них равна 1/3 величины угла АОС (по аксиоме 4.7.1.).

Доказательства теоремы о равенстве длин дуг при равенстве стягивающих их хорд и обратной теоремы.
Теорема 5.2.4.: Если длины хорд, стягивающих дуги окружностей равного радиуса, равны, то равны и длины этих дуг.
Доказательство: Пускай длины хорд АВ и СЕ, стягивающих соответствующие дуги окружности с центром в точке О и радиусом r, равны (Рис. 2). Тогда треугольники АОВ и СОЕ равны по трем сторонам (Ах. 8.5.3.), следовательно, углы АОВ и СОЕ равны по аксиоме о равенстве фигур (Ах. 6.8.).

Длина дуги окружности равна произведению ее угловой величины, выраженной в радианах, на радиус окружности [2]; угловая величина дуги равна величине центрального угла, ограничивающего эту дугу. Длина дуги АВ равна: ![]() ; длина дуги СЕ равна:
; длина дуги СЕ равна: ![]() ; при этом
; при этом ![]() , следовательно, длины дуг АВ и СЕ равны:
, следовательно, длины дуг АВ и СЕ равны: ![]() , что и требовалось доказать.
, что и требовалось доказать.

Теорема 5.2.5., обратная теореме 5.2.4.: Если длины дуг окружностей равного радиуса равны, то равны и длины хорд, стягивающих эти дуги.
Доказательство: Пускай длины дуг АВ и СЕ окружности с центром в точке О и радиусом r равны (Рис. 2). Длина дуги АВ равна: ![]() ; длина дуги СЕ равна:
; длина дуги СЕ равна: ![]() ; при этом
; при этом ![]() , следовательно,
, следовательно, ![]() . Тогда треугольники АОВ и СОЕ равны по двум сторонам и углу между ними (Ах. 8.5.1.), следовательно, хорды АВ и СЕ равны по аксиоме о равенстве фигур (Ах. 6.8.), что и требовалось доказать.
. Тогда треугольники АОВ и СОЕ равны по двум сторонам и углу между ними (Ах. 8.5.1.), следовательно, хорды АВ и СЕ равны по аксиоме о равенстве фигур (Ах. 6.8.), что и требовалось доказать.
.gif)
Примеры точного деления острых углов разной величины на три равные части.
Предложенный способ деления угла на три равные части применен к углам в 30°, 45°, 60° и 90°. Эти углы строились с помощью транспортира; деление каждого из них на три равные части проводилось только с помощью простой линейки и циркуля; результаты деления проверялись с помощью транспортира, при этом было установлено, что результаты деления – точные.
На рисунке 2 угол АОС равен 60° и разделен на три части лучами е и р; радиус ОВ в 2 раза больше радиуса ОА. Углы АОА1, А1ОА2 и А2ОС равны; величина каждого из них равна 20°, то есть 1/3 величины угла АОС. При этом дуга АС также разделена на три равные части: АА1, А1А2 и А2С.
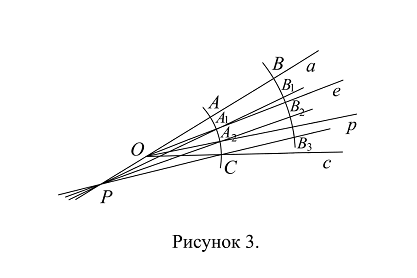
На рисунке 3 угол АОС равен 30° и разделен на три части лучами е и р; радиус ОВ в 2 раза больше радиуса ОА. Углы АОА1, А1ОА2 и А2ОС равны; величина каждого из них равна 10°, то есть 1/3 величины угла АОС. При этом дуга АС также разделена на три равные части: АА1, А1А2 и А2С.
На рисунке 4 угол АОС равен 45° и разделен на три части лучами е и р; радиус ОВ в 2 раза больше радиуса ОА. Углы АОА1, А1ОА2 и А2ОС равны; величина каждого из них равна 15°, то есть 1/3 величины угла АОС. При этом дуга АС также разделена на три равные части: АА1, А1А2 и А2С.

На рисунке 5 угол АОС равен 90° и разделен на три части лучами е и р; радиус ОВ в 2 раза больше радиуса ОА. Углы АОА1, А1ОА2 и А2ОС равны; величина каждого из них равна 30°, то есть 1/3 величины угла АОС. При этом дуга АС также разделена на три равные части: АА1, А1А2 и А2С.

Предложенным способом осуществляется деление угла на три равные части, когда отношение радиусов концентрических окружностей отлично от 2. На рисунке 6 представлен угол АОС в 60°, при этом радиус ОВ в 1,5 раза больше радиуса ОА. Углы АОА1, А1ОА2 и А2ОС равны; величина каждого из них равна 20°, то есть 1/3 величины угла АОС. При этом дуга АС также разделена на три равные части: АА1, А1А2 и А2С.

Точное деление тупого угла и соответствующей дуги окружности на три равные части по правилам классической геометрии.
Деление тупого угла на три равные части осуществляется тем же самым способом, что и деление острого угла; при этом обоснование равенства частей остается в силе. Деление тупого угла на три равные части осуществлено на примере угла в 120° (Рис. 7); радиус ОВ в 2 раза больше радиуса ОА.

На рисунке 7 угол АОС разделен лучами е и р на три угла АОА1, А1ОА2 и А2ОС; величина каждого из них равна 40°, то есть 1/3 величины угла АОС. При этом дуга АС, ограниченная сторонами исходного угла, тоже разделена на три равные части: АА1, А1А2 и А2С.
Точное деление угла и дуги окружности на пять равных частей по правилам классической геометрии.
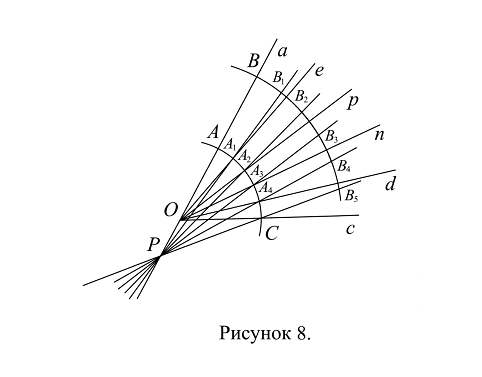
Предложенным способом осуществляется деление угла на пять равных частей, только в отличие от деления угла на три равные части, на дуге окружности с центром в точке О и радиусом 2R от точки В последовательно откладывается некоторое расстояние s пять раз, то есть раствором циркуля последовательно откладываются хорды длиной s, не достигая луча с; концы отложенных отрезков обозначаются через В1, В2, В3, В4 и В5 (Рис. 8). По теореме 5.2.4., длины дуг ВВ1, В1В2, В2В3, В3В4, В4В5, которые стягивают равные хорды ВВ1, В1В2, В2В3, В3В4 и В4В5, равны.
Через точки С и В5 проводится прямая; луч а продолжается по прямой до пересечения его с прямой СВ5, точка пересечения обозначается через Р. Затем проводятся прямые через точки Р и В1, точки Р и В2, точки Р и В3, точки Р и В4; точки пересечения этих прямых с дугой АС обозначаются через А1, А2, А3, А4 соответственно (Рис. 8).
Через точки А1, А2, А3, А4 проводятся лучи с началом в точке О, которые разбивают угол АОС на пять равных частей; лучи обозначены через е, р, п и d (Рис. 8). При этом дуга АС тоже оказывается разделенной на пять равных частей: АА1, А1А2, А2А3, А3А4 и А4С.

Равенство пяти углов, на которые разделен угол АОС, выводится так же, как и равенство построенных углов при делении исходного угла на три части, только дуг и углов будет пять, отличается и количество точек деления.
Хорды ВВ1, В1В2, В2В3, В3В4, В4В5 равны: ![]() , следовательно, по теореме 5.2.4. (доказанной в п. 2. этой статьи), длины соответствующих дуг тоже равны:
, следовательно, по теореме 5.2.4. (доказанной в п. 2. этой статьи), длины соответствующих дуг тоже равны: ![]() .
.
Окружности с центром в точке О и радиусами R и k·R являются концентрическими (Def. 5.15.1.), где ![]() ; дуги ВВ5 и АС параллельны по определению параллельных кривых, данному в [3]. По аксиоме 4.3.2. о независимости величины угла от длины его сторон, углы АРА1 и ВРВ1, углы А1РА2 и В1РВ2, углы А2РА3 и В2РВ3, углы А3РА4 и В3РВ4, углы А4РС и В4РВ5 равны:
; дуги ВВ5 и АС параллельны по определению параллельных кривых, данному в [3]. По аксиоме 4.3.2. о независимости величины угла от длины его сторон, углы АРА1 и ВРВ1, углы А1РА2 и В1РВ2, углы А2РА3 и В2РВ3, углы А3РА4 и В3РВ4, углы А4РС и В4РВ5 равны: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , при этом длины дуг ВВ1, В1В2, В2В3, В3В4, В4В5, ограниченных сторонами углов ВРВ1, В1РВ2, В2РВ3, В3РВ4, В4РВ5, равны:
, при этом длины дуг ВВ1, В1В2, В2В3, В3В4, В4В5, ограниченных сторонами углов ВРВ1, В1РВ2, В2РВ3, В3РВ4, В4РВ5, равны: ![]() , следовательно, длины дуг АА1, А1А2, А2А3, А3А4 и А4С, ограниченных сторонами углов АРА1, А1РА2, А2РА3, А3РА4 и А4РС, тоже равны – по аксиоме 6.7. о равенстве фигур:
, следовательно, длины дуг АА1, А1А2, А2А3, А3А4 и А4С, ограниченных сторонами углов АРА1, А1РА2, А2РА3, А3РА4 и А4РС, тоже равны – по аксиоме 6.7. о равенстве фигур: ![]() . Значит, дуга АС разбита на пять равных частей (Рис. 8); таким образом решена задача разделения дуги окружности на пять равных частей.
. Значит, дуга АС разбита на пять равных частей (Рис. 8); таким образом решена задача разделения дуги окружности на пять равных частей.
Длина дуги окружности равна произведению угловой величины этой дуги, выраженной в радианах, на радиус окружности [2]: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; угловая величина дуги равна величине центрального угла, стороны которого ограничивают эту дугу. Из равенства длин дуг АА1, А1А2, А2А3, А3А4 и А4С следует равенство их угловых величин:
; угловая величина дуги равна величине центрального угла, стороны которого ограничивают эту дугу. Из равенства длин дуг АА1, А1А2, А2А3, А3А4 и А4С следует равенство их угловых величин: ![]() . Равенство угловых величин дуг АА1, А1А2, А2А3, А3А4 и А4С означает равенство соответствующих им центральных углов (Рис. 8):
. Равенство угловых величин дуг АА1, А1А2, А2А3, А3А4 и А4С означает равенство соответствующих им центральных углов (Рис. 8): ![]() ; величина каждого из них равна 1/5 величины угла АОС (по аксиоме 4.7.1.).
; величина каждого из них равна 1/5 величины угла АОС (по аксиоме 4.7.1.).

Применимость разработанного способа деления угла на пять равных частей показана на примере острого угла в 60°, представленного на рисунке 8, и тупого угла в 120°, представленного на рисунке 9; тупой угол разбивается на пять равных частей так же, как и острый угол. Исходные углы АОС построены с помощью транспортира, отношение радиусов окружностей равно 2. Деление исходных углов АОС на пять равных частей проведено только с помощью простой линейки и циркуля. Результаты деления проверены с помощью транспортира: для угла в 60° величина каждого из построенных углов равна 12°, для угла в 120° величина каждого из построенных углов равна 24°, то есть в обоих случаях точно равна 1/5 величины угла АОС. При этом дуга АС тоже разделена на пять равных частей: АА1, А1А2, А2А3, А3А4 и А4С.

На рисунке 10 представлен угол АОС в 60°, при этом радиус ОВ второй окружности в 1,5 раза больше радиуса ОА. Угол АОС разделен на пять частей, величина каждого из построенных углов равна 12°, то есть 1/5 величины угла АОС. Дуга АС при этом тоже разделена на пять равных частей.

Разработанным способом может быть осуществлено деление угла и дуги окружности на большее число равных частей.
Выводы.
Разработан способ точного деления угла и дуги окружности на три равные части по правилам классической геометрии, то есть с помощью простой линейки и циркуля. Этот способ деления угла на три равные части применим к острым и тупым углам любой величины. Разработанным способом осуществляется деление угла и дуги окружности на пять и на большее число равных частей, причем как острого, так и тупого угла. Результаты деления, проверенные с помощью транспортира, точные. Задачи деления угла и дуги окружности на несколько равных частей взаимосвязаны и решаются одновременно.
Библиографический список
- Плисова Н.Н. Основания геометрии. – 4-е изд. – М.: Эдитус, 2022. – 224 с.
- Выгодский М.Я. Справочник по элементарной математике. – М.: АСТ: Астрель, 2006. – 509 с.
- Плисова Н.Н. Доказательство аксиомы о параллельных прямых, или пятого постулата Евклида // Современные научные исследования и инновации, 2019, № 7 [Электронный ресурс]. URL:https://web.snauka.ru/issues/2019/07/90006
