ДОКАЗАТЕЛЬСТВО АКСИОМЫ О ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ, ИЛИ ПЯТОГО ПОСТУЛАТА ЕВКЛИДА

 Скачать статью в формате PDF

Аксиома о параллельных прямых, или пятый постулат Евклида, является ключевой аксиомой евклидовой геометрии на плоскости. Доказательство этой аксиомы подтверждает незыблемость евклидовой геометрии. Доказательство аксиомы о параллельных прямых строится в рамках классической геометрии, без привлечения тригонометрии.
Доказательство пятого постулата Евклида в качестве теоремы основывается на аксиоматике планиметрии, что требует ее изложения. Изложение аксиоматики планиметрии требуется еще и потому, что до сих пор отсутствуют единство и системность в ее изложении. В приведенной ниже аксиоматике планиметрии даются определения геометрических элементов и указываются их свойства, специфические для геометрии; при этом общезначимые понятия, такие как: «лежать между», «лежать внутри», «быть внешним» и другие, принимаются за додефиниционное знание. Пятый постулат Евклида приводится здесь в равносильной формулировке, данной Проклом и ставшей общепринятой.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ1.0. Пространство есть единый и единственный бесконечный трехмерный объект (объект, бесконечный в трех измерениях), то есть бесконечный объем, являющийся вместимостью любых геометрических объектов. Основные свойства пространства: однородность, изотропность.
1.1. Точка есть нульмерный объект пространства, то есть объект, не имеющий пространственных измерений (объект, не имеющий протяженности ни в одном измерении).
1.2. Прямая есть бесконечный одномерный объект пространства, то есть объект, имеющий одно пространственное измерение и бесконечный в этом измерении (объект, имеющий бесконечную протяженность в длину).
1.3. Плоскость есть бесконечный двухмерный объект пространства, то есть объект, имеющий два пространственных измерения и бесконечный в обоих измерениях (объект, имеющий бесконечную протяженность в длину и ширину).
1.4. Луч есть направленная полупрямая, имеющая точку начала и продолжающаяся бесконечно. Дополнительные лучи есть полупрямые, лежащие на одной прямой и исходящие из общей точки в противоположных направлениях.
1.5. Отрезок есть часть прямой, ограниченная двумя точками, включая эти точки. Точки, ограничивающие отрезок, называются концами отрезка.
1.6. Линия (плоская) есть множество точек плоскости, образующееся в результате непрерывного перемещения точки на плоскости.
1.7. Прямая есть линия, путь вдоль которой из одной точки в любую другую является расстоянием между этими точками. Прямая есть линия, которая не искривляется.
1.8. Геометрическая фигура на плоскости (фигура) есть множество точек плоскости, образованное конечным числом линий.
1.9. Угол есть фигура, образованная двумя лучами, называемыми сторонами угла и исходящими из общей точки, называемой вершиной угла.
1.10. Ломаная линия (ломаная) есть фигура, состоящая из отрезков, последовательно соединенных своими концами так, что соседние (имеющие общую точку) отрезки не лежат на одной прямой. Отрезки называются звеньями ломаной, точки их соединения – вершинами ломаной.
1.11. Замкнутая ломаная есть ломаная, которая состоит из конечного числа отрезков и у которой начальная точка первого звена и конечная точка последнего звена совпадают; при этом первое и последнее звенья не лежат на одной прямой.
1.12. Многоугольник есть фигура, образованная замкнутой ломаной без самопересечений, все звенья которой лежат на одной плоскости. Вершины такой ломаной называются вершинами углов многоугольника, по числу которых он получает название, звенья такой ломаной называются сторонами многоугольника. Фигура, состоящая из многоугольника и его внутренней области, называется плоским многоугольником.
1.13. Окружность есть множество точек плоскости, равноудаленных от одной точки этой же плоскости, называемой центром окружности. Отрезок, соединяющий центр окружности с любой ее точкой, называется радиусом окружности.
1.14. Диаметром окружности называется отрезок, образованный двумя радиусами окружности, лежащими на дополнительных лучах.
1.15. Дуга есть часть окружности, ограниченная с двух сторон точками.АКСИОМЫ О ВЗАИМНОМ РАСПОЛОЖЕНИИ ТОЧЕК И ПРЯМЫХ2.1. Через любую точку проходит бесконечно много прямых.
2.2. Через любые две точки проходит прямая, и притом только одна.
2.3. Из трех точек на прямой одна и только одна лежит между двумя другими.
2.4. Точка, лежащая на прямой, делит эту прямую на две полупрямые, так, что: точка деления лежит между любыми двумя точками, принадлежащими разным полупрямым, и не лежит между любыми двумя точками, принадлежащими одной полупрямой.
2.5. Любая прямая разделяет плоскость на две части, называемые полуплоскостями, так, что: отрезок, соединяющий любые две точки разных полуплоскостей, пересекает эту пря­­мую, а отрезок, соединяющий любые две точки одной полуплоскости, не пересекает эту прямую.
2.6. Две прямые не могут иметь больше одной общей точки.
2.7. Пересекающимися прямыми называются две прямые, имеющие одну общую точку.
2.8. Параллельными прямыми называются две прямые на плоскости, не имеющие ни одной общей точки.
2.9. Две прямые на плоскости или пересекаются в единственной точке, или параллельны.
2.10. Перпендикулярными прямыми называются две прямые, пересекающиеся под прямым углом.
2.11. Через любую точку прямой проходит прямая, перпендикулярная данной, и притом только одна.
2.12. Через любую точку, не лежащую на данной прямой, проходит прямая, перпендикулярная данной, и притом только одна.
2.13. Через любую точку, не лежащую на данной прямой, на плоскости проходит прямая, параллельная данной, и притом только одна (аксиома о параллельных прямых, или пятый постулат Евклида).
2.14. Два отрезка называются параллельными, если они лежат на параллельных прямых.
2.15. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2.16. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
2.17. Через две параллельные прямые проходит плоскость, и притом только одна.3. АКСИОМЫ О РАССТОЯНИЯХ3.1. Любой отрезок имеет длину, большую нуля.
3.2. Длина отрезка равна сумме длин отрезков, на которые он разбивается любой внутренней точкой.
3.3. Мерой длины отрезка является длина единичного отрезка. В метрической системе мер длиной единичного отрезка является 1 миллиметр, равный 1/100 метра.
3.4. Длина отрезка равна сумме длин единичных отрезков, на которые он разбивается, включая дробные части.
3.5. Два отрезка называются равными, если они имеют одинаковую длину.
3.6. Расстоянием между двумя точками называется длина кратчайшего пути между этими точками, то есть длина отрезка, соединяющего эти точки.
3.7. Расстоянием от точки до прямой называется длина кратчайшего отрезка, соединяющего эту точку с некоторой точкой прямой, то есть длина перпендикуляра, опущенного из этой точки на прямую.
3.8. Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой.
3.9. Параллельные прямые эквидистантны (равноудалены).
3.10. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная данному отрезку и проходящая через его середину. Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
3.11. Длина отрезка одинакова, независимо от того, от какого конца отрезка она измеряется: , где точки А и В – концы отрезка АВ.АКСИОМЫ ОБ УГЛАХ4.1. Любой угол как геометрическая фигура имеет величину, большую нуля.
4.2. Величиной угла является величина поворота относительно вершины угла, совмещающего одну сторону угла с другой стороной.
4.3. Полный оборот относительно вершины, возвращающий сторону угла в исходное положение, в градусной системе мер углов составляет 360°, в радианной системе мер составляет 2π.
4.4. Полным углом называется угол, величина которого равна полному обороту, что в градусной системе мер составляет 360°, в радианной системе мер составляет 2π.
4.5. Угловой мерой является единичный угол, в градусной системе мер составляющий 1/360 полного угла.
4.6. Величина угла равна сумме величин углов, на которые он разбивается любым лучом, исходящим из его вершины и проходящим между его сторонами; при этом стороны угла лежат на разных полуплоскостях, образованных прямой, одной из полупрямых которой является данный луч.
4.7. Величина угла равна сумме величин единичных углов, на которые он разбивается, включая дробные части.
4.8. Два угла называются равными, если они имеют одинаковую угловую меру.
4.9. Биссектрисой угла называется луч, исходящий из вершины угла, проходящий между его сторонами и делящий угол пополам; при этом стороны угла лежат на разных полуплоскостях, образованных прямой, одной из полупрямых которой является данный луч.
4.10. Прямым углом называется угол, равный ¼ полного угла, что в градусной системе мер составляет 90°, в радианной системе мер составляет π/2.
4.11. Развернутым углом называется угол, стороны которого образованы дополнительными лучами. Развернутый угол равен ½ полного угла, что в градусной системе мер составляет 180°, в радианной системе мер составляет π.
4.12. Две пересекающиеся прямые образуют четыре угла. Угол между пересекающимися прямыми есть угол между лучами, не являющимися дополнительными друг другу. Углом между пересекающимися прямыми обычно считается острый угол.
4.13. Параллельные прямые не образуют угла. Угол между двумя параллельными прямыми принимается равным нулю, или же равным π.
4.15. Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие их стороны являются дополнительными лучами. Два смежных угла в сумме составляют развернутый угол.
4.16. Два угла называются дополнительными, если они имеют общую вершину и общие стороны и в сумме составляют полный угол.
4.17. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Вертикальные углы равны.
4.18. Прямой угол есть угол, равный смежному с ним углу.
4.19. Угол, меньший прямого, называется острым, больший прямого – тупым.
4.20. Величина угла одинакова, независимо от того, какая из его сторон совмещается с другой стороной: , где а и b – лучи, образующие .АКСИОМЫ О ВЗАИМНЫХ РАСПОЛОЖЕНИЯХ ОКРУЖНОСТЕЙ И ПРЯМЫХ5.1. Прямая может: пересекать окружность в двух точках и не проходить через ее центр; пересекать окружность в двух точках и проходить через ее центр; касаться окружности; не иметь общих точек с окружностью.
5.2.1. Прямая, имеющая с окружностью две общие точки и не проходящая через ее центр, называется секущей.
5.2.2. Отрезок секущей, лежащий внутри окружности, называется хордой.
5.2.3. Прямая и окружность имеют две общие точки, если расстояние от центра окружности до прямой меньше радиуса окружности.
5.3. Если прямая имеет с окружностью две общие точки и проходит через центр окружности, то хорда совпадает с диаметром окружности.
5.4.1. Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности. Касательная перпендикулярна радиусу, проведенному к точке касания.
5.4.2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
5.5. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
5.6. Центральным углом называется угол, образованный двумя радиусами. Величина центрального угла не зависит от длины радиуса. Если центральные углы, образованные равными радиусами, опираются на равные хорды, то они равны.
5.7. Длина дуги, заключенной между концами двух радиусов, пропорциональна величине центрального угла, образованного этими радиусами.
5.8. Вписанным углом называется угол, образованный двумя хордами, исходящими из одной точки окружности.
5.9. Описанным углом называется угол, образованный двумя касательными к окружности, исходящими из одной точки.
5.10. Две окружности могут: пресекаться в двух точках; касаться в одной точке; не иметь общих точек; быть концентрическими.
5.11. Расстоянием между двумя окружностями называется расстояние между их центрами.
5.12.1. Две окружности называются пересекающимися, если они имеют две общие точки.
5.12.2. Если расстояние между двумя окружностями меньше суммы и больше разности их радиусов, то окружности пересекаются.
5.13.1. Две окружности называются касающимися, если они имеют одну общую точку, называемую точкой касания.
5.13.2. Если расстояние между окружностями равно сумме их радиусов, то происходит внешнее касание окружностей.
5.13.3. Если расстояние между окружностями равно разности их радиусов, то происходит внутреннее касание окружностей.
5.14.1. Две окружности называются непересекающимися, если они не имеют общих точек.
5.14.2. Две окружности не пересекаются, если расстояние между ними больше суммы их радиусов.
5.15.1. Две окружности, центры которых совпадают, а радиусы не равны, называются концентрическими. Две концентрические окружности не пересекаются.
5.15.2. Две окружности являются концентрическими, если расстояние между ними равно нулю.АКСИОМЫ О НАЛОЖЕНИИ, РАВЕНСТВЕ И ПОДОБИИ ФИГУР6.1. Под наложением фигур понимается наложение на чертеж одной фигуры копии чертежа другой фигуры, нанесенной на прозрачный материальный носитель.
6.2. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
6.3. Любой угол (ab) можно совместить наложением с равным ему углом (cd) двумя способами: так, что луч а совместится с лучом с, а луч b – с лучом d; так, что луч а совместится с лучом d, а луч b – с лучом с.
6.4.1. Две фигуры называются равными, если они имеют одинаковые форму и размеры.
6.4.2. Две фигуры называются равными, если их можно совместить наложением.
6.4.3. Две фигуры F и F₁ называются равными, если существует движение, преобразующее фигуру F в фигуру F₁, то есть каждой точке фигуры F ставящее в соответствие некоторую точку фигуры F₁.
6.5. Любая фигура равна самой себе.
6.6. Если фигура F равна фигуре F₁, то фигура F₁ равна фигуре F.
6.7. Если фигура F равна фигуре F₁, а фигура F₁ равна фигуре F₂, то фигура F равна фигуре F₂.
6.8. Если фигура F равна фигуре F₁, то все элементы фигуры F равны соответственным элементам фигуры F₁.
6.9. Если все задающие фигуру элементы фигуры F равны соответственным элементам фигуры F₁, то фигура F равна фигуре F₁.
6.10. Если все элементы фигуры F равны соответственным элементам фигуры F₁, то фигура F равна фигуре F₁.
6.11. Подобием называется преобразование плоскости, изменяющее все расстояния меж­ду точками в одном и том же отношении k>0, то есть для любых двух точек А и В и их образов А₁ и В₁ справедливо равенство: А₁В₁=k·АВ; число k называется коэффициентом подобия.
6.12. Две фигуры F и F₁ называются подобными, если существует преобразование подобия, при котором фигура F преобразуется в фигуру F₁, то есть каждой точке фигуры F ставится в соответствие некоторая точка фигуры F₁.АКСИОМЫ ДВИЖЕНИЯ ПЛОСКОСТИ7.1. На плоскости определено преобразование f, если каждой точке А плоскости ставится в соответствие единственная точка  той же плоскости; при этом точка А₁ называется образом точки А, а точка А – прообразом точки А₁.
7.2. Движением называется преобразование плоскости, при котором для любых двух точек А и В и их образов А₁ и В₁ справедливо равенство: АВ=А₁В₁, то есть расстояние между образами равно расстоянию между прообразами.
7.3. Виды движения плоскости: осевая симметрия; центральная симметрия; поворот; параллельный перенос.
7.4. Осевой симметрией плоскости с осью симметрии а называется преобразование плоскости, при котором прямая а остается на месте, а каждой точке А ставится в соответствие такая точка , что прямая а является серединным перпендикуляром к отрезку . Обозначение:  – осевая симметрия с осью а.
7.5. Центральной симметрией плоскости с центром симметрии в точке О называется преобразование плоскости, при котором точка О остается на месте, а каждой точке А ставится в соответствие такая точка , что точка О является серединой отрезка . Обозначение:  – центральная симметрия относительно точки О.
7.6. Поворотом плоскости с центром поворота в точке О и углом поворота φ называется преобразование плоскости, при котором точка О остается на месте, а каждой точке А ставится в соответствие такая точка , что  и . Обозначение:  – поворот относительно точки О на угол φ. Угол поворота, в отличие от угла как геометрической фигуры, может быть как положительным, так и отрицательным; угол поворота положителен, если поворот совершается против часовой стрелки.
7.7. Параллельным переносом плоскости на вектор  называется преобразование плоскости, при котором каждой точке А ставится в соответствие такая точка , что .
7.8. Движение инволютивно: преобразование плоскости, обратное данному виду движения, тоже является движением.
7.9. Композиция двух движений тоже является движением.
7.10.1. Движение плоскости сохраняет: расстояние между любыми двумя точками плоскости; простое отношение трех точек прямой; отношение «лежать между».
7.10.2. Движение плоскости отображает: прямую – на прямую; отрезок – на равный ему отрезок; луч – на луч; угол – на равный ему угол; параллельные прямые – на параллельные прямые; вектор – на вектор.АКСИОМЫ О ТРЕУГОЛЬНИКАХ8.1.1. Треугольник есть фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой.
8.1.2. Треугольник есть многоугольник с тремя углами.
8.2.1. Условие существования треугольника, называемое неравенством треугольника: каждая сторона треугольника меньше суммы двух других его сторон.
8.2.2. Три неравенства треугольника могут быть сведены к одному: чтобы три отрезка могли служить сторонами треугольника, необходимо, чтобы больший из них был меньше суммы двух других.
8.3. Классификация треугольников осуществляется по величинам углов и по длинам сторон.
8.3.1. По величинам углов различаются треугольники: остроугольный треугольник, в котором все углы – острые; тупоугольный треугольник, в котором один угол – тупой; прямоугольный треугольник, в котором один угол – прямой.
8.3.2. По длинам сторон различаются треугольники: разносторонний треугольник, в котором нет равных сторон; равнобедренный треугольник, в котором две стороны равны; равносторонний треугольник, в котором все стороны равны.
8.4. Свойства элементов треугольника: против большей стороны лежит больший угол; против большего угла лежит большая сторона; против равных сторон лежат равные углы; против равных углов лежат равные стороны.
8.5. Признаки равенства треугольников:
8.5.1. Первый признак: если две стороны и угол между ними одного треугольника равны двум соответственным сторонам и углу между ними другого треугольника, то такие треугольники равны.
8.5.2. Второй признак: если сторона и два прилежащих угла одного треугольника равны соответственным стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
8.5.3. Третий признак: если три стороны одного треугольника равны соответственным сторонам другого треугольника (если каждая сторона одного треугольника равна соответственной стороне другого треугольника), то такие треугольники равны.
8.6. Подобными называются треугольники, соответственные углы которых равны, а сто­ро­ны одного треугольника пропорциональны соответственным сторонам другого треугольника.
8.7. Признаки подобия треугольников:
8.7.1. Первый признак: если два угла одного треугольника равны двум соответственным углам другого треугольника, то такие треугольники подобны.
8.7.2. Второй признак: если две стороны одного треугольника пропорциональны двум соответственным сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
8.7.3. Третий признак: если три стороны одного треугольника пропорциональны соответственным сторонам другого треугольника, то такие треугольники подобны.ПРАВИЛА ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ В КЛАССИЧЕСКОЙ ГЕОМЕТРИИ9.1. В классической геометрии построения выполняются простой линейкой (не имеющей шкалы) и циркулем.
9.2. С помощью линейки проводятся: произвольная прямая; произвольная прямая, проходящая через данную точку; прямая, проходящая через две данные точки.
9.3. С помощью циркуля: проводится окружность произвольного радиуса; проводится из данного центра окружность данного радиуса; откладывается отрезок на данной прямой от данной или произвольной точки.
9.4. Основным условием возможности геометрического построения фигуры по заданным элементам является измерение расстояния.
9.5. Расстояние измеряется раствором циркуля. Результатом измерения циркулем рассто­яния является проведение окружности или ее дуги с радиусом, равным измеренному расстоянию.
9.6. Величины углов непосредственно не измеряются; их величины определяются опосредованно в соответствии с основными свойствами циркуля как инструмента измерения.
9.7. Эмпирические свойства циркуля:
9.7.1. Циркуль с ненулевым раствором образует угол с равными сторонами.
9.7.2. Если положить циркуль на плоскость чертежа, то концы циркуля при изменении угла его раствора вычерчивают дугу окружности с радиусом, равным длине сторон циркуля. Расстояние между концами циркуля является хордой, стягивающей эту дугу.
9.7.3. Вместе с измеряемым отрезком циркуль образует равнобедренный треугольник.
9.7.4. Бoльшая ширина раствора циркуля образует больший угол раствора циркуля и наоборот.
9.7.5. Если два измеряемых циркулем отрезка равны, то равны ширина и угол раствора циркуля.
9.7.6. Если при измерении длин отрезков ширина и угол раствора циркуля равны, то измеряемые отрезки равны.
9.8. Результаты построения единственны:
9.8.1. На любой прямой или на любом луче от данной точки можно отложить отрезок, равный данному, и притом только один.
9.8.2. От любого луча в заданную полуплоскость можно отложить угол, равный данному, и притом только один.

Постановка задачиТеорема: Через любую точку, не лежащую на данной прямой, на плоскости проходит прямая, параллельная данной, и притом только одна (Ax. 2.13.).Дано: прямая а; точка В, не лежащая на прямой а.
Задача: Доказать, что через точку В проходит единственная прямая b, параллельная прямой а.

Доказательство:Проведение прямой, перпендикулярной данной и проходящей через данную точкуЗадача: Провести прямую, проходящую через точку В и перпендикулярную прямой а.
Построение: Опустить перпендикуляр из точки В на прямую а значит провести через точку В серединный перпендикуляр к отрезку на прямой а (Def. 3.10.).

Проводим дугу окружности с центром в точке В и радиусом r так, чтобы она пересекла прямую а в двух точках (Ax. 5.1., 5.2.3.); обозначаем точки пересечения через С и М (Рис. 1).
Проводим окружность с центром в точке С и радиусом СВ, которая проходит через точку В (Ax. 5.2.1.). Проводим окружность с центром в точке М и радиусом МВ=СВ, которая проходит через точку В и пересекается с предыдущей окружностью (Ax. 5.10.); точку пересечения окружностей в другой по отношению к точке В полуплоскости, образуемой прямой а, обозначаем через В₁.
Проводим через точки В и В₁ прямую и обозначаем ее через с (Ax. 2.2.); обозначаем точку пересечения прямой с с прямой а через А (Def. 2.7.); обозначаем точку пересечения прямой с с дугой через Е (Ax. 5.1.).
Нужно доказать, что прямая с перпендикулярна прямой а. Радиусы окружностей равны: , следовательно,  по трем сторонам (Ax. 8.5.3.), следовательно, по аксиоме о равенстве фигур (Ax. 6.8.): , значит, . Отсюда следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит,  (Ax. 6.8.); эти углы – смежные (Def. 4.15.), то есть: , следовательно, , то есть эти углы – прямые (Def. 4.10.); это значит, что прямая с перпендикулярна прямой а (Def. 2.10.).

Прямая с, проходящая через точку В и перпендикулярная прямой а, проведена.Доказательство единственности перпендикуляра, опущенного из данной точки на данную прямуюЗадача: Доказать, что прямая с, проходящая через точку В и перпендикулярная прямой а (п. II, 1.1.), единственна.
Доказательство: Предположим, что прямая с не единственна и существует прямая с₁, отлич­ная от прямой с, которая проходит через точку В и перпендикулярна прямой а. Это значит, что прямая с₁ проходит через точку В и не проходит через точку А (Ax. 2.6.); обозна­чаем точку пересечения прямых с₁ и а через А₁. Проводим дугу окружности с центром в точке В и радиусом ВА₁, пересекающую прямую с (Ax. 5.1., 5.4.2.); обозначаем точку пересе­чения дуги и прямой с через К (Рис. 2). Проводим дугу окружности с центром в точке В и радиусом ВА до пересечения ее с прямой с₁; обозначаем точку пересечения через L (Ax. 9.5.).

, то есть наклонная длиннее перпендикуляра.
,
,
то есть  не является кратчайшим отрезком между точкой В и прямой а; значит, прямая с₁ является наклонной к прямой а, а не перпендикуляром к ней, что противоречит сделанному предположению об их перпендикулярности. Предположение о том, что прямая с₁, отличная от прямой с, перпендикулярна прямой а, приводит к противоречию, значит, оно неверно. Следовательно, прямая с, проходящая через точку В и перпендикулярная прямой а, единственна, что и требовалось доказать.

Аксиома о единственности перпендикуляра, опущенного из данной точки на данную прямую (Ax. 2.12.), доказана.
Проведение прямой, перпендикулярной первому перпендикуляруЗадача: Восставить серединный перпендикуляр из точки В, лежащей на прямой с, к прямой с (п. II, 1.1.).
Построение (Рис. 3): Проводим окружность с центром в точке В и радиусом ВА, пересекающуюся с прямой с в точке А и второй точке, которую обозначаем через Р (Ax. 5.3.); при этом ВА=ВР (Def. 1.13.). Проводим окружность с центром в точке А и радиусом АР=2ВА (Def. 1.14.); проводим окружность с центром в точке Р и радиусом РА=АР, пересекающуюся с предыдущей (Ax. 5.10.); обозначаем точки пересечения окружностей через О и Q. Через точки О и В проводим прямую и обозначаем ее через b (Ax. 2.2.).

Нужно доказать, что прямая b перпендикулярна прямой с. Радиусы окружности с центром в точке А: АО=АР и окружности с центром в точке Р: РО=РА=АР равны: АО=РО, при том что ВА=ВР. Следовательно,  по трем сторонам (Ax. 8.5.3.), значит,  по аксиоме о равенстве фигур (Ax. 6.8.); эти углы являются смежными (Def. 4.15.), то есть: , следовательно, , то есть эти углы являются прямыми (Def. 4.10.). Прямая b является серединным перпендикуляром к отрезку РА (Def. 3.10.). Все эти утверждения справедливы и при рассмотрении точки Q вместо точки О. Перпендикулярность прямых b и с (Def. 2.10.) доказана.

Прямая b, проходящая через точку В и перпендикулярная прямой с, проведена.Доказательство единственности перпендикуляра, восставленного из данной точки прямой к этой прямойЗадача: Доказать, что прямая b, проходящая через точку В и перпендикулярная прямой с (п. II, 2.1.), единственна.
Доказательство: Предположим, что прямая b не единственна и существует прямая b₁, отличная от прямой b и перпендикулярная прямой с.
Так как прямая b₁ отлична от прямой b, то она проходит через точку В, но не проходит через точку О (Ax. 2.6.), то есть не проходит через точку пересечения окружностей с центрами в точках Р и А и радиусами РА и АР. Обозначаем точки пересечения прямой b₁: с окружностью с центром в точке Р и радиусом РА через Т и R, с окружностью с центром в точке А и радиусом АР через S и U (Рис. 4).
Точка S отлична от точки T, следовательно:
; ; следовательно:
 и ; значит:
 и  (противоречие Ax. 6.9.); следовательно:
 и , иначе для треугольников выполнялось бы равенство по двум сторонам и углу между ними (Ax. 8.5.1.);
 и , так как эти углы смежные (Def. 4.15.), следовательно:
 и ,
то есть прямая b₁ не перпендикулярна прямой с (противоречие Def. 4.10.), что противоречит предположению об их перпендикулярности. Предположение о том, что прямая b не единственна и существует прямая b₁, отличная от прямой b и перпендикулярная прямой с, приводит к противоречию, следовательно, оно неверно. Следовательно, прямая b, проходя­щая через точку В и перпендикулярная прямой с, единственна, что и требовалось доказать.

Аксиома о единственности перпендикуляра, восставленного из данной точки прямой к этой прямой (Ax. 2.11.), доказана.
Доказательство независимой теоремы о сумме внутренних углов в треугольнике
Задача: Определить сумму внутренних углов в треугольнике независимым способом.
I вариант решения
Решение: Построим произвольный треугольник ABC. Обозначим стороны треугольника ABC через а, b и c; обозначим внутренние углы треугольника цифрами. Из вершины треугольника : продолжим стороны треугольника а и b во внешнюю область треугольника; восставим перпендикуляр l к продолжению стороны а и перпендикуляр m к продолжению стороны b; опустим перпендикуляр k на сторону с (Рис. 7).
На сторону АС перпендикуляр опускается следующим образом (Рис. 5): проводим дугу окружности с центром в точке В и радиусом ВА до пересечения ее со стороной АС; обозначаем точку пересечения через D. Проводим дугу окружности с центром в точке А и радиусом АВ в другой полуплоскости, образуемой прямой с, по отношению к точке В; проводим дугу окружности с центром в точке D и радиусом DВ=АВ до пересечения ее с предыдущей дугой; обозначаем точку пересечения дуг через Р. Через точки В и Р проводим прямую (Ax. 2.2.), являющуюся серединным перпендикуляром к АD (Def. 3.10.), и обозначаем ее через k; обозначаем точку пересечения прямой k со стороной AС через К. Доказательство перпендикулярности прямых приведено ниже.

К стороне а перпендикуляр l восставляется следующим образом (Рис. 6). Проводим окружность с центром в точке В и произвольным радиусом r, пересекающуюся с прямой а в двух точках, которые обозначаем через К и L. Проводим дугу окружности с центром в точке К и радиусом КL, затем проводим дугу окружности с центром в точке L и радиусом LК до пересечения ее с предыдущей дугой; точку пересечения дуг обозначаем через N. Через точки В и N проводим прямую и обозначаем ее через l.  по трем сторонам (Ax. 8.5.3.), следовательно,  по аксиоме о равенстве фигур (Ax. 6.8.). Эти углы являются смежными (Def. 4.15.): , следовательно, они являются прямыми (Ax. 4.10.). Это значит, что прямая l перпендикулярна прямой а. К стороне b треугольника перпендикуляр восставляется таким же способом.

Углы между перпендикулярами (Рис. 7) в сумме составляют развернутый угол (Def. 4.11.), следовательно, по теореме о равенстве угла между двумя пересекающимися прямыми углу между прямыми, перпендикулярными данным (доказательство этой теоремы дано в п. II, 4.1.), сумма внутренних углов в треугольнике равна половине полного угла (Def. 4.4.):

;
;
;
;
.
Так как рассматривался произвольный треугольник, то равенство суммы внутренних уг­­лов в треугольнике половине полного угла справедливо для любого треугольника. Задача решена.
II вариант решения
Решение: Построим произвольный . Во внутренней области этого треугольника выберем произвольную точку О. Из точки О опустим перпендикуляры k, l, m на каждую из сторон треугольника.
На сторону АС перпендикуляр опускается следующим образом (Рис. 8): проводим дугу окружности с центром в точке О и радиусом ОА до пересечения ее с АС; обозначаем точку пересечения через D. Проводим дугу окружности с центром в точке А и радиусом АО, проходящую через точку О и пересекающую АС. Проводим дугу окружности с центром в точке D и радиусом DО=АО, проходящую через точку O и пересекающую сторону АС; обозначаем точку пересечения дуг через Р. Через точки О и Р проводим прямую (Ax. 2.2.), являющуюся серединным перпендикуляром к АD (Def. 3.10.), до пересечения ее со стороной ВС; обозначаем прямую ОР через k и точку пересечения прямой ОР со стороной AС через К. Доказательство перпендикулярности прямой ОК стороне АС дано в п. II, 1.1.
На две другие стороны треугольника перпендикуляры OL и ON опускаются таким же способом.

Угол между двумя пересекающимися прямыми равен углу между прямыми, перпендикулярными данным (доказательство этой теоремы дано в п. II, 4.1.). Углы между перпендикулярами, пересекающимися в точке О, равны соответственным углам треугольника (Рис. 9), при том что вертикальные углы равны (доказательство этой теоремы дано в п. II, 4.2.).
Углы между перпендикулярами, равные соответственным углам треугольника, в совокупности образуют развернутый угол (Def. 4.11.), то есть суммируются (Ax. 4.6.). Следовательно, углы в треугольнике также суммируются и может быть определена их сумма:

Сумма внутренних углов в треугольнике равна π, или половине полного угла. Так как рассматривался произвольный треугольник, то равенство суммы внутренних углов в треугольнике половине полного угла справедливо для любого треугольника. В данном варианте доказательства и треугольник, и способ доказательства отличны от приведенных в I варианте доказательства, но результат одинаков в обоих случаях, следовательно, сумма углов в треугольнике является постоянной величиной. Задача решена.
Сформулируем теорему: Сумма внутренних углов в любом треугольнике равна половине полного угла. Теорема доказана.
4.1. Доказательство равенства угла между двумя прямыми углу между перпендикулярными им прямыми
Теорема: Угол между двумя прямыми равен углу между перпендикулярными им прямыми.
Дано: Прямые а и b, пересекающиеся в точке О под произвольным углом.
Задача: Доказать, что углы между двумя пересекающимися прямыми и прямыми, перпендикулярными им, равны.
Доказательство:
1) Случай, когда точка пересечения перпендикуляров совпадает с точкой пересечения данных прямых.
Из точки О – точки пересечения прямых а и b – восставим перпендикуляр с к прямой а и перпендикуляр d к прямой b. Перпендикуляр с восставляется следующим образом: Прово­дим окружность с центром в точке О и произвольным радиусом r так, чтобы она пересекала прямую а в двух точках – К и L (Рис. 10). Проводим дугу окружности с центром в точке К и радиусом КL; проводим дугу окружности с центром в точке L и радиусом LK; точку пере­сечения дуг обозначаем через N. Через точки О и N проводим прямую (Ax. 2.2.) и обозначаем ее через с.  по трем сторонам (Ax. 8.5.3.), следовательно,  (Ax. 6.8.). Так как эти углы – смежные, то есть в сумме равны π (Def. 4.15.), то они являются прямыми, то есть равными  (Def. 4.10.). Перпендикулярность прямых а и с доказана.

Перпендикуляр d к прямой b из точки О восставляется таким же способом.
Обозначим углы между прямыми цифрами и определим соотношение между ними (Рис. 11):

.
Угол между пересекающимися прямыми равен углу между перпендикулярными им прямыми, что и требовалось доказать.
2) Случай, когда точка пересечения перпендикуляров не совпадает с точкой пересечения данных прямых, но при этом лежит на одной из них.
На прямой b выбираем произвольную точку . Из точки  опускаем перпендикуляр c на прямую а и восставляем перпендикуляр d к прямой b.
Перпендикуляр c на прямую а опускается следующим образом (Рис. 12): Проводим окружность с центром в точке  и произвольным радиусом , пересекающую прямую а в двух точках – С и М. В другой полуплоскости по отношению к точке  относительно прямой а проводим дугу окружности с центром в точке С и радиусом  и дугу окружности с центром в точке М и радиусом = до пересечения ее с предыдущей дугой; точку пересечения дуг обозначаем через . Через точки  и  проводим прямую и обозначаем ее через c, точку пересечения прямых c и а обозначаем через .

Нужно доказать, что прямая c перпендикулярна прямой а. Радиусы окружностей равны: , следовательно,  по трем сторонам (Ax. 8.5.3.), следовательно, по аксиоме о равенстве фигур (Ax. 6.8.): , значит, . Отсюда следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит,  (Ax. 6.8.); эти углы – смежные (Def. 4.15.), то есть: , следовательно, , то есть эти углы – прямые (Def. 4.10.); это значит, что прямая c перпендикулярна прямой а (Def. 2.10.).

Перпендикуляр d к прямой b восставляется следующим образом (Рис. 12): проводим окружность с центром в точке  и произвольным радиусом , пересекающую прямую b в двух точках – K и L. Проводим дугу окружности с центром в точке К и радиусом KL, затем дугу окружности с центром в точке L и радиусом LK до ее пересечения с предыдущей дугой; точку пересечения дуг обозначаем через N . Через точки  и N проводим прямую и обозначаем ее через d.  по трем сторонам (Ax. 8.5.3.), следовательно,  (Ax. 6.8.). Так как эти углы – смежные (Def. 4.15.), то они являются прямыми (Def. 4.10., 4.18.). Перпендикулярность прямых d и b доказана.

Из точки  восставляем перпендикуляр  к прямой c следующим образом. Проводим окружность с центром в точке  и произвольным радиусом R, пересекающую прямую c в двух точках, которые обозначаем через G и J (Рис. 13). Проводим дугу окружности с центром в точке G и радиусом GJ; проводим дугу окружности с центром в точке J и радиусом JG; точку пересечения дуг обозначаем через F. Через точки  и F проводим прямую (Ax. 2.2.) и обозначаем ее через .  по трем сторонам (Ax. 8.5.3.), следовательно,  по аксиоме о равенстве фигур (Ax. 6.8.); так как эти углы – смежные (Def. 4.15.): , то они являются прямыми, то есть равными  (Def. 4.10., 4.18.). Перпендикулярность прямых  и c доказана.

Углы между прямыми а и c и  и c равны и являются прямыми. От прямой  откладываем угол с вершиной в точке , равный углу между прямыми а и b (Рис. 14). Для этого проводим дугу окружности с центром в точке О и произвольным радиусом ОА, пересекающую прямую а в точке А и прямую b в точке В. Проводим дугу окружности с центром в точке  и радиусом ОА, пересекающую прямую  в точке . Проводим дугу окружности с центром в точке А и радиусом АВ, пересекающую дугу  в точке В. Проводим дугу окружности с центром в точке  и радиусом АВ, пересекающую предыдущую дугу окружности с центром в точке  и радиусом ОА в точке ; при этом точка  принадлежит прямой b. Действительно, если от прямой b отложить угол , для чего провести дугу окружности с центром в точке  и радиусом ВА, то эта дуга пересечется с дугой  в точке , лежащей на прямой , то есть . Это доказывается тем, что .
 по трем сторонам (Ax. 8.5.3.), следовательно,  по аксиоме о равенстве фигур (Ax. 6.8.), то есть угол между прямыми  и b равен углу между прямыми а и b.

Далее определяются величины углов с вершинами в точке  между прямыми c и d и между прямыми а и b (Рис. 14).

Угол между пересекающимися прямыми равен углу между перпендикулярными им прямыми, что и требовалось доказать.
3) Случай, когда точка пересечения перпендикуляров не совпадает с точкой пересечения данных прямых и не лежит ни на одной из них.
Во внутренней области угла между прямыми а и b выбираем произвольную точку . Из точки  опускаем перпендикуляр c на прямую а и перпендикуляр d на прямую b. Перпендикуляр c на прямую а опускается так: проводим окружность с центром в точке  и произвольным радиусом , пересекающую прямую а в двух точках – С и М (Рис. 15). В другой полуплоскости по отношению к точке  проводим дугу окружности с центром в точке С и радиусом  и дугу окружности с центром в точке М и радиусом = до пересечения ее с предыдущей дугой; точку пересечения дуг обозначаем через . Через точки  и  проводим прямую и обозначаем ее через c; точку пересечения прямой c с прямой а обозначаем через А₁.

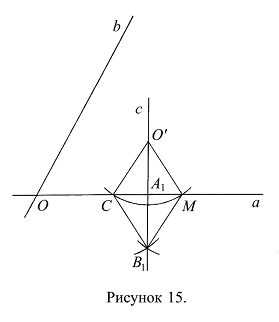
Нужно доказать, что прямая c перпендикулярна прямой а. Радиусы окружностей равны: , следовательно,  по трем сторонам (Ax. 8.5.3.), следовательно, по аксиоме о равенстве фигур (Ax. 6.8.): , значит, . Отсюда следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит,  (Ax. 6.8.); эти углы – смежные (Def. 4.15.), то есть: , следовательно, , то есть эти углы – прямые (Def. 4.10.); это значит, что прямая c перпендикулярна прямой а (Def. 2.10.).

Перпендикуляр d на прямую b опускается таким же образом.
Из точки  восставляем перпендикуляр  к прямой c; перпендикуляр восставляется так же, как и в п. II, 4.1.2., где дано доказательство перпендикулярности этих прямых. Углы между прямыми а и c и  и c равны и являются прямыми.
От прямой  откладываем угол с вершиной в точке , равный углу между прямыми а и b (Рис. 16). Для этого проводим дугу окружности с центром в точке О и произвольным радиусом ОА, пересекающую прямую а в точке А и прямую b в точке В. Проводим дугу окружности с центром в точке  и радиусом ОА, пересекающую прямую  в точке . Проводим дугу окружности с центром в точке А и радиусом АВ, пересекающую дугу  в точке В. Проводим дугу окружности с центром в точке  и радиусом АВ, пересекающую предыдущую дугу окружности с центром в точке  и радиусом ОА в точке . Через точки  и  проводим прямую и обозначаем ее через .  по трем сторонам (Ax. 8.5.3.), следовательно,  по аксиоме о равенстве фигур (Ax. 6.8.), то есть угол между прямыми  и  равен углу между прямыми а и b.

Нужно доказать, что прямая d перпендикулярна прямой . Предположим, что прямая d не перпендикулярна прямой . Тогда существует прямая , отличная от прямой d, которая перпендикулярна прямой  и при этом проходит через точку . По аксиоме 2.12. о единственности опущенного перпендикуляра, прямая  не перпендикулярна прямой b и, следовательно, пересекается с ней в точке , отличной от точки D (Рис. 17).
От прямой  откладываем угол с вершиной в точке  и величиной, равной фактической величине угла  (по построению). Для этого проводим дугу окружности с центром в точке  и произвольным радиусом , пересекающую прямую  в точке Е и прямую c – в точке Н. Проводим дугу окружности с центром в точке  и радиусом , пересекающую прямую  в точке . Проводим дугу окружности с центром в точке Е и радиусом ЕН, пересекающую дугу  в точке Н. Проводим дугу окружности с центром в точке  и тем же радиусом ЕН, которая пересекается с дугой окружности с центром в точке  и радиусом  в точке . Через точки  и  проводим прямую и обозначаем ее через  (Рис. 17).  по трем сторонам (Ax. 8.5.3.), следовательно,  по аксиоме о равенстве фигур (Ax. 6.8.), значит, построенный угол равен исходному: .

Далее, от прямой  откладываем угол с вершиной в точке  и величиной, равной величине угла . Для этого проводим дугу окружности с центром в точке  и радиусом , пересекающую прямую  в точке Q. Проводим дугу окружности с центром в точке  и радиусом , пересекающую прямую b в точке . Проводим дугу окружности с центром в точке H и радиусом НQ, пересекающую дугу  в точке Q. Проводим дугу окружности с центром в точке  и тем же радиусом НQ, которая пересекается с дугой окружности с центром в точке  и радиусом  в точке  (Рис. 17). При этом точка  – точка пересечения этих дуг – лежит на прямой b, что объясняется следующим: то, что прямая c перпендикулярна прямой а, задает ориентацию откладываемых углов относительно прямых а и b – помимо равенства величин откладываемых углов величинам исходных; при этом величина откладываемого угла связана с величиной угла между прямыми а и b: . Если откладывать углы от прямой b в обратной последовательности, то точка пересечения последних дуг – точка  – будет лежать на прямой , так как:  и .  по трем сторонам (Ax. 8.5.3.), следовательно,  по аксиоме о равенстве фигур (Ax. 6.8.), значит, построенный угол равен исходному: .
Проводим расчет величины угла между прямыми c и  в точке  исходя из предположения о перпендикулярности прямых  и :
.
Проводим расчет величины угла между прямыми b и  в точке  с учетом рассчитанной величины угла между прямыми c и  в точке :
,
то есть прямые b и  перпендикулярны, что противоречит выводу о том, что прямая  не перпендикулярна прямой b, следующему из предположения о том, что прямая d, являющаяся опущенным на прямую b перпендикуляром, не перпендикулярна прямой , а перпендикулярна ей прямая . Предположение о том, что прямая d не перпендикулярна прямой , приводит к противоречию, следовательно, оно неверно, следовательно, прямая d перпендикулярна прямой .

Далее определяются величины углов с вершинами в точке  между прямыми c и d и между прямыми а и b (Рис. 16).

Угол между пересекающимися прямыми равен углу между перпендикулярными им прямыми, что и требовалось доказать.
Если точка  – точка пересечения перпендикуляров – лежит во внешней области острого угла между прямыми а и b, иначе, во внутренней области угла, смежного с углом между прямыми а и b (Рис. 18), то теорема справедлива и в этом случае; доказательство – то же самое, что и приведенное выше.

Так как угол между прямыми а и b – произвольный, то случай равенства нулю угла между прямыми а и b, то есть случай их совпадения или параллельности (Ax. 4.13.), может рассматриваться как частный случай данной теоремы.
Итак, доказано следующее:

Теорема о равенстве углов между двумя прямыми и перпендикулярными им прямыми доказана.Обоснование равенства нулю угла между совпадающими и параллельными прямымиЗадача: Обосновать, что угол между совпадающими прямыми a и b равен нулю.Обоснование:

б) Задача: Обосновать, что угол между параллельными прямыми a и b равен нулю (Ax. 4.13.).
Обоснование:

Так как понятие угла между прямыми существует и в планиметрии вводится именно для прямых, то из вариантов: угол «равен нулю» или угол «не существует» для решения геометрических задач требуется первый вариант. Если угол между пересекающимися прямыми стремится к нулю и достигает нуля, то прямые совпадают; это действие не противоречит аксиоматике планиметрии. Если затем осуществить параллельный перенос одной из совпадающих прямых, то получатся параллельные прямые; это действие не противоречит аксиоматике планиметрии.
4.3. Доказательство равенства вертикальных углов
Дано: Две пересекающиеся прямые a и b, угол  между ними.
Задача: Доказать, что вертикальные углы (Def. 4.17.):  и , а также  и , попарно равны (Рис. 19).

Доказательство:

Вертикальные углы равны, что и требовалось доказать.
5.1. Доказательство теоремы о том, что прямая, перпендикулярная перпендикуляру к данной прямой, параллельна данной прямой
Задача: Доказать, что прямая b, проходящая через точку В, не лежащую на прямой а, и перпендикулярная перпендикуляру с к данной прямой а, параллельна прямой а (пп. II, 1.1. – 2.2.).
I вариант доказательства
Доказательство: Предположим, что прямые а и b пересекаются (Def. 2.7.); обозначаем точку их пересечения через D. Следовательно, образуется  (Def. 8.1.1.) (Рис. 20).

Чтобы существовал, необходимо, чтобы выполнялось неравенство треугольника (Ax. 8.2.2.): . Так как прямые а и b бесконечны (Def. 1.2.), то существуют любые  и , такие, что они могут удовлетворять неравенству треугольника (Ax. 8.2.2.). Следовательно, если прямые а и b пересекаются, то  существует по трем сторонам.
Проверим, существует ли по углам:
, согласно п. II, 1.1.;
, согласно п. II, 2.1.;
, согласно теореме п. II, 3., то есть:
, или, что – то же самое: .
а) Если , то это противоречит предположению о том, что прямые а и b пересекаются и образуют угол (Ax. 4.12.);
б) Если , то это противоречит теореме о сумме углов в треугольнике, Т.II, 3.
Предположение о том, что прямые а и b пересекаются, приводит к противоречию, следовательно, оно неверно, следовательно, по Ax. 2.9. прямые а и b параллельны (Def. 2.8.), что и требовалось доказать.


Расстояние  не определялось и может быть любым (Def. 1.2.), значит, предположение о пересечении прямых а и b приводит к противоречию при любом , то есть при любой удаленности точки предполагаемого пересечения прямых от точек А и В. Следовательно, прямые а и b параллельны.
II вариант доказательства
Доказательство: Согласно теореме II, 4.1., угол между двумя прямыми равен углу между перпендикулярными им прямыми; угол между параллельными прямыми равен нулю (Ax. 4.13.). Для прямых а и b, перпендикулярных прямой с, имеем:

Доказательство без использования аксиомы 4.13.:

Параллельность прямых а и b доказана.
Сформулируем теорему: Если две прямые перпендикулярны одной и той же третьей прямой, то эти прямые параллельны. Теорема доказана.
5.2. Доказательство единственности прямой, проходящей через данную точку и параллельной данной прямой
Задача: Доказать, что прямая b, проходящая через точку В, не лежащую на прямой а, и параллельная прямой а, единственна (п. II., 5.1.).
I вариант доказательства
Доказательство: Предположим, что прямая b не единственна и существует прямая b₁, отличная от прямой b, проходящая через точку В и параллельная прямой а. Так как прямая b проходит через точки В и О (п. II, 2.1.), то прямая  проходит через точку В и точку О₁, отличную от точки О.
Прямая а перпендикулярна прямой с, точка их пересечения – А (п. II, 1.1.); прямая b перпендикулярна прямой с, точка их пересечения – В (п. II, 2.1.). Возьмем на прямой а произвольную точку D; точка D выбирается в той же полуплоскости, образуемой прямой с, в которой находится точка О₁ (Рис. 21). .
Так как прямая  отлична от прямой b, то: , следовательно, , следовательно, может существовать , где  – точка пересечения прямых  и а.
Так как прямая b перпендикулярна прямой с, то: .

 существует:
1) по сторонам, так как прямые  и а бесконечны (Def. 1.2.), следовательно, существуют такие  и , что выполняется неравенство треугольника (Ax. 8.2.2.): ;
2) по углам, при том, что сумма углов в треугольнике равна π (теорема II, 3.):
,
то есть прямые  и а пересекаются (Ax. 4.12.), что противоречит предположению об их параллельности. Предположение о существовании прямой b₁, отличной от прямой b и параллельной прямой а, приводит к противоречию, следовательно, оно неверно. Следовательно, прямая b, проходящая через точку В и параллельная прямой а, единственна, что и требовалось доказать.


II вариант доказательства
Доказательство: Предположим, что прямая b не единственна и существует прямая b₁, отличная от прямой b, проходящая через точку В и параллельная прямой а. Так как прямая b проходит через точки В и О (п. II, 2.1.), то прямая  проходит через точку В и точку О₁, отличную от точки О.

Прямая а перпендикулярна прямой с, точка их пересечения – А (п. II, 1.1.); прямая b перпендикулярна прямой с, точка их пересечения – В (п. II, 2.1.). Так как угол между прямыми b и  не равен нулю, то прямая  перпендикулярна прямой d, отличной от прямой c (Рис. 22). Согласно теореме II, 4.1., угол между прямыми а и  равен углу между перпендикулярными им прямыми с и d и, следовательно, не равен нулю. Следовательно, прямые а и  пересекаются (Ax. 4.12.), что противоречит предположению об их параллельности. Предположение о существовании прямой b₁, отличной от прямой b и параллельной прямой а, приводит к противоречию, следовательно, оно неверно. Следовательно, прямая b, проходящая через точку В и параллельная прямой а, единственна, что и требовалось доказать.

Аксиома о параллельных прямых (Ax. 2.13.), или пятый постулат Евклида, доказана.6. Доказательство свойства равноудаленности параллельных прямыхТеорема: Параллельные прямые эквидистантны (равноудалены) (Ax. 3.9.).
Дано: Параллельные прямые а и b.
Задача: Доказать, что расстояние между параллельными прямыми а и b постоянно.

6.1. Доказательство существования прямоугольника
На прямой b берем произвольную точку В и опускаем из нее перпендикуляр на прямую а; обозначаем перпендикуляр через с и точку пересечения прямых с и а через А (Рис. 23); порядок построения перпендикуляра и доказательство перпендикулярности прямых с и а приведены в п. II, 1.1. Угол  – прямой по построению.

Нужно доказать, что прямая с перпендикулярна прямой b. Предположим, что прямая с не перпендикулярна прямой b; следовательно, существует прямая d, отличная от прямой с, которая перпендикулярна прямой b и проходит через точку В (Рис. 24). По теореме II, 4.1.: угол между прямыми а и b равен углу между соответственно перпендикулярными им прямыми с и d, угол между которыми не равен нулю. По аксиоме 4.12. это значит, что прямые а и b пересекаются, что противоречит условию их параллельности. Предположение о том, что пря­мая с не перпендикулярна прямой b, приводит к противоречию, следовательно, оно невер­­но, следовательно, прямая с перпендикулярна прямой b. Это значит, что угол  – прямой.

На прямой b берем произвольную точку Н и опускаем из нее перпендикуляр на прямую а; обозначаем перпендикуляр через n и точку пересечения прямых n и а – через F.
Перпендикуляр n на прямую а опускается следующим образом: проводим дугу окружности с центром в точке H и произвольным радиусом , пересекающую прямую а в двух точках – К и N (Рис. 23). В другой полуплоскости по отношению к точке Н относительно прямой а проводим дугу окружности с центром в точке К и радиусом КН и дугу окружности с центром в точке N и радиусом NН=КН до пересечения ее с предыдущей дугой; точку пересечения дуг обозначаем через Р. Через точки Н и Р проводим прямую и обозначаем ее через n, точку пересечения прямых n и а обозначаем через F.
Нужно доказать, что прямая n перпендикулярна прямой а. Радиусы окружностей равны: , следовательно,  по трем сторонам (Ax. 8.5.3.), следовательно, по аксиоме о равенстве фигур (Ax. 6.8.): , значит, . Отсюда следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит,  (Ax. 6.8.); эти углы – смежные (Def. 4.15.), то есть: , следовательно, , то есть эти углы – прямые (Def. 4.10.); это значит, что прямая n перпендикулярна прямой а (Def. 2.10.).

Угол  – прямой по построению. Нужно доказать, что прямая n перпендикулярна прямой b. Предположим, что прямая n не перпендикулярна прямой b; следовательно, существует прямая p, отличная от прямой n, которая перпендикулярна прямой b и проходит через точку H (Рис. 24). По теореме II, 4.1.: угол между прямыми а и b равен углу между соответственно перпендикулярными им прямыми n и p, угол между которыми не равен нулю. По аксиоме 4.12. это значит, что прямые а и b пересекаются, что противоречит условию их параллельности. Предположение о том, что прямая n не перпендикулярна прямой b, приводит к противоречию, следовательно, оно неверно, следовательно, прямая n перпендикулярна прямой b. Это значит, что угол  – прямой.
Прямая с перпендикулярна прямой а и прямая n перпендикулярна прямой а. По теореме II, 5.1.: прямые с и n, перпендикулярные одной и той же прямой а, параллельны. Аналогично этому, прямая с перпендикулярна прямой b и прямая n перпендикулярна прямой b. По теореме II, 5.1. это значит, что прямые с и n параллельны.
Таким образом, существует прямоугольник ABHF, в котором все углы – прямые и противоположные стороны параллельны. («Гипотеза острого угла» не может иметь места).

6.2. Доказательство равноудаленности параллельных прямых
Рассмотрим прямоугольник ABHF (п. 6.1.).
Нужно доказать, что , где  и – расстояния между параллельными прямыми а и b в разных точках (Def. 3.8.). Проводим диагональ AH прямоугольника ABHF (Рис. 25).

, , так как они являются внутренними накрест лежащими углами (доказательство независимым способом теоремы о попарном равенстве внутренних накрест лежащих углов дано в п. II, 7.).  по стороне АH и двум прилежащим углам (Ax. 8.5.2.), следовательно,  по аксиоме о равенстве фигур (Ax. 6.8.). Так как точка H выбрана произвольно, то равенство расстояния между прямыми а и b в разных точках:  справедливо для любого, то есть справедливо на всем протяжении прямых (Def. 1.2., 1.7.), что и требовалось доказать.

Аксиома о равноудаленности параллельных прямых (Ax. 3.9.) доказана.
7. Доказательство независимой теоремы о попарном равенстве внутренних накрест лежащих углов
Задача: Доказать, что при пересечении двух параллельных прямых a и b третьей прямой c, называемой секущей, внутренние накрест лежащие углы попарно равны.
Углы 1 и 4, 2 и 3 на Рис. 26 называются внутренними накрест лежащими углами.

Нужно доказать, что  и .
I вариант доказательства
Доказательство: Из точки А – точки пересечения прямых с и а – опускаем перпендикуляр d на прямую b (Рис. 27), точку пересечения прямых обозначаем через В; порядок построения перпендикуляра и доказательство перпендикулярности прямых даны в пп. II, 1.1., 6.1.
Нужно доказать, что прямая d перпендикулярна прямой а. Предположим, что прямая d не перпендикулярна прямой а; следовательно, существует прямая n, отличная от прямой d, перпендикулярная прямой а и проходящая через точку А (Рис. 27). По теореме II, 4.1.: угол между прямыми а и b равен углу между прямыми n и d и, следовательно, не равен нулю; согласно аксиоме 4.12., это означает, что прямые а и b пересекаются, что противоречит условию об их параллельности. Предположение о том, что прямая d не перпендикулярна прямой а, приводит к противоречию, следовательно, оно неверно, следовательно, прямая d перпендикулярна прямой а.

Из точки С – точки пересечения прямых с и b – опускаем перпендикуляр е на прямую а, точку пересечения прямых обозначаем через Е (Рис. 27); порядок построения перпендикуляра и доказательство перпендикулярности прямых даны в пп. II, 1.1., 6.1.
Нужно доказать, что прямая е перпендикулярна прямой b. Предположим, что прямая е не перпендикулярна прямой b; следовательно, существует прямая р, отличная от прямой е, перпендикулярная прямой b и проходящая через точку С. По теореме II, 4.1.: угол между прямыми а и b равен углу между прямыми e и р и, следовательно, не равен нулю; согласно аксиоме 4.12., это означает, что прямые а и b пересекаются, что противоречит условию об их параллельности. Предположение о том, что прямая е не перпендикулярна прямой b, приводит к противоречию, следовательно, оно неверно, следовательно, прямая е перпендикулярна прямой b.
В итоге образуется прямоугольник АВСЕ, так как все углы в нем – прямые.

Рассмотрим прямоугольник АВСЕ. Проведем диагональ АС этого прямоугольника (Рис. 28) и обозначим его углы цифрами – в соответствии с нумерацией внутренних накрест лежащих углов на Рис. 26. При этом:  и .
.


,
то есть внутренние накрест лежащие углы попарно равны, что и требовалось доказать.
II вариант доказательства
Обозначаем внутренние накрест лежащие углы цифрами (Рис. 26):

Предположим, что угол между прямыми b и с, расположенный в пространстве между прямыми а и b, не равен углу между прямыми а и с. Тогда вторая сторона угла с вершиной в точке С, одной из сторон которого является прямая b и который равен углу между прямыми а и с, не лежит на прямой с, а лежит на прямой d, отличной от прямой с (Рис. 29).

Из точки С опускаем на прямую а перпендикуляр и обозначаем его через n (Рис. 29); порядок построения перпендикуляра и доказательство перпендикулярности прямых даны в пп. II, 1.1., 3., 6.1.

Нужно доказать, что прямая n перпендикулярна прямой b. Предположим, что прямая n не перпендикулярна прямой b; следовательно, существует прямая p, отличная от прямой n, перпендикулярная прямой b и проходящая через точку C. По теореме II, 4.1.: угол между прямыми а и b равен углу между прямыми n и p и, следовательно, не равен нулю; согласно аксиоме 4.12., это означает, что прямые а и b пересекаются, что противоречит условию об их параллельности. Предположение о том, что прямая n не перпендикулярна прямой b, приводит к противоречию, следовательно, оно неверно, следовательно, прямая n перпендикулярна прямой b.

Из точки С восставляем перпендикуляр k к прямой d и перпендикуляр l к прямой с (Рис. 29); порядок построения перпендикуляра и доказательство перпендикулярности прямых даны в пп. II, 2.1., 3., 4.1.

Применяем теорему II, 4.1. о равенстве угла между двумя прямыми углу между перпендикулярными им прямыми:

,
то есть внутренние накрест лежащие углы попарно равны, что и требовалось доказать.
Теорема о попарном равенстве внутренних накрест лежащих углов, образующихся при пересечении двух параллельных прямых секущей, доказана в рамках классической геометрии и без использования аксиомы о параллельных прямых.
Из равенства внутренних накрест лежащих углов следует равенство соответственных и внешних накрест лежащих углов – в силу равенства вертикальных углов.
8. Доказательство независимой теоремы о сумме внутренних углов в четырехугольнике
Задача: Определить сумму внутренних углов в четырехугольнике.
Решение: Рассмотрим произвольный четырехугольник ABCD. В его внутренней области выберем произвольную точку О и опустим из нее перпендикуляры k, l, m, n на каждую сторону четырехугольника (Рис. 31). Перпендикуляры проводятся как серединные перпендикуляры к отрезкам на сторонах четырехугольника (Def. 3.10.). На сторону АD перпендикуляр k опускается следующим образом (Рис. 30): проводим дугу окружности с центром в точке O и произвольным радиусом r, пересекающую сторону АD в двух точках; обозначаем точки пересечения через E и F. Проводим дугу окружности с центром в точке E и радиусом EO в другой полуплоскости, образуемой прямой AD, по отношению к точке O; проводим дугу окружности с центром в точке F и радиусом FO=EO до пересечения ее с предыдущей дугой; обозначаем точку пересечения дуг через G. Через точки O и G проводим прямую (Ax. 2.2.) и обозначаем ее через k; обозначаем точку пересечения прямой k со стороной AD через H.

Нужно доказать, что прямая k перпендикулярна стороне AD. Радиусы окружностей равны: , следовательно,  по трем сторонам (Ax. 8.5.3.), следовательно, по аксиоме о равенстве фигур (Ax. 6.8.): , значит, . Отсюда следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит,  (Ax. 6.8.); эти углы – смежные (Def. 4.15.), то есть: , следовательно, , то есть эти углы – прямые (Def. 4.10.); это значит, что прямая k является серединным перпендикуляром к отрезку EF (Def. 3.10.) и, следовательно, перпендикулярна отрезку AD.

Перпендикуляры l, m, n на стороны АВ, ВС и CD соответственно опускаются таким же образом.
.
Угол между двумя пересекающимися прямыми равен углу между прямыми, перпендикулярными данным (по теореме II, 4.1.). Углы между перпендикулярами к сторонам четырехугольника с вершинами в точке О равны соответственным углам четырехугольника (Рис. 31):

.
Углы между перпендикулярами образуют полный угол (Def. 4.4.), то есть суммируются (Ax. 4.6.). Следовательно, углы в четырехугольнике также суммируются и в сумме составляют полный угол:
.
Так как рассматривался произвольный четырехугольник, то равенство суммы внутренних углов в четырехугольнике полному углу справедливо для любого четырехугольника. Задача решена.

Сформулируем теорему: Сумма внутренних углов в четырехугольнике равна полному углу. Теорема доказана.
Выводы. В разделе II доказаны:
Аксиома о единственности перпендикуляра, опущенного на прямую (п. 1.2.);
Аксиома о единственности перпендикуляра, восставленного к прямой (п. 2.2.);
Теорема о равенстве суммы углов в треугольнике половине полного угла (п. 3.);
Теорема о равенстве углов между двумя прямыми и перпендикулярами к ним (п. 4.1.);
Аксиома о равенстве вертикальных углов (п. 4.3.);
Теорема о параллельности прямых, перпендикулярных одной и той же прямой (п. 5.1.);
Аксиома о параллельных прямых, или пятый постулат Евклида (пп. 1.1. – 5.2.);
Аксиома об эквидистантности параллельных прямых (п. 6.);
Теорема о попарном равенстве внутренних накрест лежащих углов (п. 7.);
Теорема о равенстве суммы углов в четырехугольнике полному углу (п. 8.).

Считается, что Лобачевским открыта неевклидова геометрия. В работе «Геометрические исследования по теории параллельных линий», изданной в 1840 году, Лобачевский резюмирует свои взгляды по вопросу о параллельных прямых и свои гипотетические построения, которые он сам называет «воображаемой геометрией». Приведем цитаты из этой работы.

Со стр. 39 Лобачевский начинает выдвигать утверждения, отличные от положений, принятых в геометрии:
Обсуждение: а) Лобачевский допускает существование «двух классов прямых», проходящих через точку, не лежащую на данной прямой: пересекающих данную прямую и непересекающих ее. Но согласно аксиоме Ax 2.9., две прямые могут: или иметь одну общую точку и, значит, пересекаться (Def. 2.7.), или не иметь ни одной общей точки и, значит, быть параллельными (Def. 2.8.). Аксиомы планиметрии взаимосвязаны: Ax. 2.9. обобщает Ax. 2.6. о том, что две прямые не могут иметь больше одной общей точки, а аксиома 2.6. является следствием аксиомы 2.2., согласно которой, через любые две точки проходит единственная прямая. Утверждение Лобачевского противоречит этим аксиомам геометрии.
б) Ни одного математического доказательства своего утверждения Лобачевский не дает, а ссылается только на свой рисунок, на котором точка пересечения непараллельных прямых не видна. На это можно возразить следующее: если некоторые элементы не умещаются на чертеже, следует уменьшить масштаб.
в) Свое утверждение Лобачевский иллюстрирует рисунком (Черт. 1). На его рисунке отрезки АН и АG не пересекают прямую DC, то есть Лобачевский демонстрирует непонимание того, что прямая бесконечна (Def. 1.2.).
Утверждение сторонников Лобачевского о том, что пятый постулат Евклида «имеет локальный характер», а не требует рассмотрения всей бесконечной прямой, не соответствует действительности. Оно противоречит не только аксиоматике планиметрии в ее современной форме, но и «Началам» Евклида. В книге I «Начал» Евклид дает такое определение параллельных прямых: «23. Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той, ни с другой стороны между собой не встречаются». Выражение «будучи продолжены неограниченно» означает именно бесконечность прямых. Далее, второй постулат Евклида в той же книге I гласит: «2. Ограниченную прямую можно непрерывно продолжать по прямой/прямо», что также определяет прямую как бесконечную. Сам пятый постулат в этой же книге сформулирован так: «И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых». Здесь также есть формулировка «продолженные неограниченно», что означает бесконечность прямых и отнюдь не локальный характер этого постулата. Когда Евклид говорит об отрезках, он употребляет словосочетание «ограниченная прямая» или же без слова «ограниченная» использует буквенные обозначения, выражающие ограниченность отрезка двумя точками, например: «Предложение 1 (29, 30): На данной ограниченной прямой построить равносторонний треугольник. Пусть данная точка будет А, заданная же прямая ВС; требуется от точки А отложить прямую, равную данной прямой ВС». Можно еще добавить, что хотя любое рассмотрение проводится на ограниченном участке прямой, но произвольный выбор участка для рассмотрения означает справедливость приводимых доказательств для всей прямой, так как ее свойства едины на всем ее протяжении.
г) На самом деле, Лобачевский вместо прямых (Def. 1.2.) рассматривает отрезки (Def. 1.5.) и ставит задачу на определение условий существования прямоугольного треугольника по катету и гипотенузе и углу между ними, намеренно задавая при этом условия, делающие построение треугольника невозможным. Эта задача не связана с пятым постулатом Евклида (Ax. 2.13.) и отнюдь его не отменяет.
Утверждение Лобачевского противоречит и определению параллельных отрезков (Def. 2.14.). Аксиома о параллельных прямых в данном случае выполняется для параллельных отрезков, понятие которых остается в силе: через данную точку, не лежащую на данном отрезке, проходит единственный отрезок, параллельный данному.
д) Лобачевский осуществляет подмену понятий (под прямыми подразумевает отрезки), нарушая тем самым логический закон тождества. В научной работе должны соблюдаться однозначность принятых в этой науке понятий и точность в их употреблении.
Цитируем Лобачевского далее. По поводу своего чертежа 1 он заявляет (стр. 40):

Обсуждение: е) Лобачевский выдвигает без доказательств предположение о том, что существует некий угол параллельности, то есть угол между параллелью и перпендикуляром к данной прямой, зависящий от расстояния между параллельными. Бездоказательность и необоснованность утверждения являются нарушением логического закона достаточного основания. На самом деле, параллельность прямых не зависит от расстояния между ними (Ax. 2.13.): аксиома о параллельных справедлива для любой прямой, проходящей через любую точку, находящуюся на любом расстоянии от данной прямой. Аналогично этому, согласно аксиоме Ax. 2.12., через любую точку, находящуюся на любом расстоянии от данной прямой, проходит перпендикуляр к данной прямой. Предположение о неравенстве угла между параллелью и перпендикуляром прямому углу противоречит не только аксиоме о единственности параллельной прямой (Ax. 2.13.), но и аксиоме о единственности опущенного (Ax. 2.12.) и восставленного перпендикуляров (Ax. 2.11.). Гипотеза Лобачевского противоречит сразу нескольким аксиомам планиметрии.
Цитируем далее (стр. 43):

Доказательство, даваемое Лобачевским этому положению, опускаем из-за ограниченности объема данной статьи, но вывод, который Лобачевский делает в результате, нужно привести (стр. 43):

ж) Это и есть основная гипотеза Лобачевского, доказательств которой он не дает, но которую кладет в основу своих теоретических построений. Предположение, противоречащее только что доказанному им самим утверждению, является нарушением сразу двух логических законов: достаточного основания и закона противоречия.
Далее Лобачевский отрицает равенство 2π суммы углов в четырехугольнике и параллельность противоположных сторон в прямоугольнике (стр. 48) со всеми вытекающими отсюда последствиями.
Утверждение о независимости пятого постулата Евклида от других аксиом неверно. Отрицание этого постулата противоречит не только указанным в пп. а) и е) аксиомам, но и понятиям: параллельных прямых (Def. 2.8., Ax. 4.13.), параллельных отрезков (Def. 2.14.), пересекающихся прямых (Def. 2.7., Ax. 4.12.), накрест лежащих углов (п. II, 7.), а также понятию прямого угла (Def. 4.10., 4.18.), что влечет за собой нарушение всей аксиоматики планиметрии, представляющей собой единую систему.
Цитируем Лобачевского далее (стр. 46):

Доказательство опускаем; в итоге Лобачевский утверждает следующее (стр.46):

з) Таким образом, «воображаемая геометрия» Лобачевского целиком основывается на постулируемом им и ничем не обоснованном предположении, что сумма углов в треугольнике меньше π и что существует «угол параллельности», зависящий от расстояния между прямыми и меньший π/2. Это не более чем гипотеза. Необоснованность и бездоказательность выдвигаемого утверждения является нарушением логического закона достаточного основания.
Цитируем Лобачевского далее (стр. 47):

Разберем это подробно.
Для удобства заменим в обозначениях букв штрихи на индексы, заново сделаем чертеж (Черт. 10.2) и введем следующие обозначения:
.

Рассмотрим и посчитаем сумму углов в нем:  (1).
Левая часть уравнения (1) представляет собой расчет суммы углов в конкретном, правая часть уравнения (1) представляет собой общее значение суммы углов в любом треугольнике, согласно п. 20) цитируемой работы Лобачевского.
Из уравнения (1) следует: .
Рассмотрим и посчитаем сумму углов в нем:  (2).
Посчитаем левую часть уравнения (2): ,
что и утверждает Лобачевский в п. 23). Но левая часть уравнения должна быть приравнена правой части:  (2.2) .
Для проверки рассмотрим и посчитаем сумму углов в нем:
 (3);
;
 (3.2) .
Значит, сумма углов в треугольнике равна π и не может быть другой. Если же Лобачевский допускает, что сумма углов в треугольнике не является постоянной величиной и может отличаться в разных треугольниках, но при этом всегда должна быть меньше π, то расчет суммы углов в  опровергает это предположение Лобачевского: в нем сумма углов равна , если . Расчет суммы углов в  сделан на основании предположения Лобачевского о том, что сумма углов в  равна . Следовательно, сама гипотеза Лобачевского приводит к внутреннему противоречию в его теоретических построениях.
Таким образом, доказано, что предположение Лобачевского о том, что сумма углов в треугольнике равна , то есть меньше π, ошибочно, что доказывается в рамках построений, сделанных самим Лобачевским. Здесь же доказано от противного, что сумма углов в треугольнике равна π. В своем выводе к п. 22) Лобачевский утверждает, что из предположения о том, что сумма углов в треугольнике меньше π, следует, что существует «угол параллельности» П(р)< π/2. На этих двух предположениях Лобачевский строит свою «воображаемую геометрию». Но так как первое предположение Лобачевского ошибочно, то ошибочно и второе, так как оно следует из первого.
Вывод. Гипотеза Лобачевского ненаучна и неверна.

Попытка создания Лобачевским неевклидовой геометрии имела отрицательные последствия для науки. Она спровоцировала появление целого теоретического направления, модернистского по своей сути, ставящего целью вытеснение евклидовой геометрии неевклидовыми, выдаваемыми за передовые научные достижения, что ведет к ниспровержению научных основ в математике.
В качестве примеров неевклидовой геометрии приводятся следующие модели.
Проективная модель геометрии Лобачевского на плоскости есть геометрия внутри круга, за исключением ограничивающей его окружности. При этом такой круг называется «плоскостью», «прямой» называется любая хорда с исключенными концами, точкой называется точка внутри круга (Рис. IV, 1, [14]). Аналогично в пространстве определяется геометрия Лобачевского как геометрия внутри шара, выраженная в тех же условных наименованиях. При этом утверждается, что аксиома о параллельных прямых здесь не выполняется: через точку внутри круга, не лежащую на данной хорде («прямой»), проходит сколь угодно много непересекающих ее хорд («прямых»). Во-первых, в этой модели используются другие геометрические элементы – отрезки (Def. 1.5.) – по сравнению с аксиомой о параллельных прямых 2.13., где речь идет именно о прямых, имеющих свое определение (Def. 1.2.). Эта модель – задача на определение существования треугольника по трем задающим его элементам. Во-вторых, даже в такой модели (призванной любыми средствами поддержать «воображаемую геометрию» Лобачевского) выполняется аксиома о параллельных прямых (Ax. 2.13.): хорда, параллельная данной хорде, единственна, так как сохраняется понятие параллельных отрезков (Def. 2.14.). Это признак коллинеарности векторов в векторной алгебре. В аналитической геометрии определяется условие, при котором две аналитически заданные прямые пересекаются. Классическая геометрия, аналитическая геометрия, дифференциальная геометрия составляют научную систему, в отрыве от которой не может рассматриваться никакая геометрическая модель. Таким образом, данная модель является частным случаем евклидовой геометрии (иначе и быть не может, так как «воображаемая геометрия» Лобачевского ошибочна).

В модели Пуанкаре (Рис. IV, 2, [14]) за плоскость Лобачевского принимается внутренняя область круга, под прямыми (Def. 1.2.) понимаются дуги окружностей (Def. 1.15.), перпендикулярных окружности данного круга, под движением (Def. 7.2.) понимается комбинация инверсий и таким образом осуществляется подмена понятий, то есть используется прием, недопустимый в любой дискуссии, а тем более в научной. К аксиоме о параллельных прямых (Ax. 2.13.) эта модель отношения не имеет, а является иллюстрацией аксиомы 5.14.2.: две окружности не пересекаются, если расстояние между ними больше суммы их радиусов.

В подобных моделях нарушается логический закон тождества. Евклидова геометрия, весь ее понятийный аппарат первичны по отношению к любой другой геометрической теории; эта последняя должна следовать принятой в науке терминологии, если она претендует на научность (в отличие от сенсационности). Каждый геометрический элемент имеет четкое и однозначное определение, что лежит в основе единства научной терминологии и научных представлений.
В качестве еще одного примера неевклидовой геометрии приводится сферическая геометрия. В ней отмечается такое отличие от евклидовой геометрии: через две точки, являющиеся диаметрально противоположными, проходит бесконечно много сферических прямых (а не одна). Также утверждается, что на сфере в диаметрально противоположных точках происходит пересечение сферических прямых, перпендикулярных одной и той же третьей сферической прямой (Рис. IV, 3, [5]), то есть якобы нарушается теорема о параллельности двух прямых, перпендикулярных одной и той же прямой. Эти примеры трактуются как примеры отличия сферической геометрии от евклидовой. На самом деле, отличия нет: во-первых, здесь также осуществляется подмена понятий – под «сферическими прямыми» понимаются большие полуокружности, под «отрезками» – дуги больших полуокружностей; именно эти термины и должны использоваться, будучи первичными, и именно к ним должны применяться соответствующие аксиомы; во-вторых, аксиома 2.2. евклидовой геометрии здесь выполняется: через две точки, даже диаметрально противоположные, прямая (в научном смысле – Def. 1.2., а не как условное наименование другого геометрического элемента), проходит одна.
В геометрии сложилась единая система понятий и терминологии, произвольное обращение с которой недопустимо, как и в любой другой науке.

Что касается теоремы о параллельности прямых, перпендикулярных одной и той же прямой, то здесь аналогия (при том, что это всего лишь аналогия) проведена некорректно: две большие полуокружности, пересекающиеся в диаметрально противоположных точках, не могут считаться аналогом параллельных прямых, так как не отвечают определению параллельных прямых – не иметь общей точки, а только локально удовлетворяют свойству параллельных прямых быть перпендикулярными одной и той же прямой. Аналогом параллельных прямых могут служить концентрические окружности (Def. 5.15.1.) – они не имеют общей точки, что соответствует определению параллельных прямых (при том, что центры окружностей не лежат на самих окружностях), и обладают свойством эквидистантности (по абсолютному значению), а также обладают свойством быть перпендикулярными одной и той же прямой – любой прямой, проходящей через их общий центр. Но аналог не должен подменять оригинал. Концентрические окружности являются примером параллельных кривых, но не параллельных прямых (как проекции сечений конуса параллельными плоскостями на одну плоскость, параллельную этим плоскостям). Для концентрических окружностей как параллельных кривых выполняется аналог аксиомы о параллельных прямых: через точку, не лежащую на данной окружности и отличную от ее центра, проходит единственная окружность, концентрическая с данной, то есть параллельная ей. Доказывается это от противного: можно выдвинуть предположение о пересечении в данной точке двух окружностей; окружности пересекаются, если расстояние между ними меньше суммы и больше разности их радиусов (Ax. 5.12.2.); отсюда следует, что одна из них не является концентрической с данной (противоречие Ax. 5.15.2.), следовательно, окружность, проходящая через данную точку и концентрическая с данной, единственна.
Сферическая геометрия отлична не от евклидовой геометрии, а от евклидовой планиметрии, что закономерно, так как сферическая геометрия является геометрией кривых, причем пространственных, то есть относится к области стереометрии. Но евклидова планиметрия лежит в основе любой геометрической теории. Сферическая тригонометрия основана на классической тригонометрии.
Считается, что на псевдосфере имеет место геометрия Лобачевского, если точки и прямые на конечном участке плоскости Лобачевского сопоставить с точками и геодезическими линиями на псевдосфере. Такова модель, предложенная Бельтрами в работе «Опыт интерпретации неевклидовой геометрии». В этой модели перемещение фигуры, например, геодезического треугольника, по псевдосфере сопоставляется с движением плоской фигуры на плоскости, при котором она остается равной самой себе. Но Бельтрами уточняет, что это равенство относится только к длине линий и величине углов, тогда как абсолютная кривизна линий не входит в его рассмотрение. Более того, Бельтрами пишет следующее (стр. 207): чтобы геодезическим линиям поверхности в его модели соответствовали прямые линии на плоскости, эти поверхности должны быть поверхностями постоянной сферической, то есть положительной кривизны, тогда как псевдосфера является поверхностью отрицательной кривизны. Причем это соответствие Бельтрами выводит, используя первую квадратичную форму, однако кривизна кривой не может быть вычислена на основе знания только первой квадратичной формы. Чтобы применить свою модель к поверхности постоянной отрицательной кривизны, Бельтрами полагает радиус кривизны мнимым (стр. 208). И только делая столько допущений, Бельтрами утверждает (стр. 190), что «через всякую точку поверхности всегда можно провести две геодезические линии, параллельные одной и той же геодезической линии…», не давая при этом четких критериев параллельности геодезических.
Должно быть дано определение параллельных кривых на поверхности. Можно ввести такое определение: кривая  на участке между точками  и  и кривая  на участке между точками  и , лежащие на одной и той же поверхности σ, параллельны, если единичный вектор касательной к кривой  в каждой ее точке на рассматриваемом участке коллинеарен вектору, являющемуся образом единичного вектора касательной к кривой  на рассматриваемом участке в ее точке, соответственной точке кривой , в результате непараллельного переноса его на вектор, соединяющий две соответственные точки кривых.
Если обозначить через  единичный вектор касательной к пространственной кривой  в точке , лежащей между точками  и  или совпадающей с любой из них, через  – его образ как результат непараллельного переноса вектора  в точку , а через  – единичный вектор касательной к пространственной кривой  в точке , соответственной точке , то кривые  и  параллельны на рассматриваемых участках, если векторы  и  коллинеарны: .
Непараллельный перенос является композицией параллельного переноса на вектор  пары векторов – единичного вектора касательной  и вектора главной нормали  к кривой  в точке , жестко связанных между собой, при котором образами этих векторов становятся соответственно векторы  и , а точкой их приложения становится точка кривой  – точка , соответственная точке , и поворота относительно точки  вектора  вместе с жестко связанным с ним вектором , в результате которого образ вектора  становится коллинеарным вектору  – вектору главной нормали к кривой  в точке .
Две плоские кривые параллельны на рассматриваемых участках, то есть отвечают определению параллельных кривых, если окружности, соприкасающиеся с кривыми  и  в точках  и  соответственно, являются концентрическими или являются образом и прообразом в результате параллельного переноса.
Если рассматриваемая поверхность является поверхностью вращения, то она имеет характеристические образующие и направляющие – окружности. Направляющая поверхности вращения должна считаться таковой, если нормаль к плоскости, на которой она лежит, проведенная через любую точку этой плоскости, параллельна оси вращения.
Псевдосфера является поверхностью вращения трактрисы относительно оси абсцисс. Образующей псевдосферы является трактриса, направляющей – окружность. Направляющие псевдосферы соответствуют определению параллельных кривых на поверхности, образующие – нет.
Рассмотрим три геодезические линии на псевдосфере. Исходную геодезическую обозначим через ; две геодезические, пересекающиеся в точке, не принадлежащей , которую обозначим через , обозначим через  и . Для двух геодезических, пересекающихся в одной точке, имеем: в точке  угол между вектором касательной к геодезической  –  и вектором касательной к геодезической  –  не равен нулю: , следовательно, если одна из этих геодезических, пусть это будет , параллельна исходной геодезической , то есть удовлетворяет введенному определению параллельных кривых, то вторая геодезическая –  – этому определению не удовлетворяет: . Следовательно, утверждение о том, что через точку, не лежащую на данной геодезической, проходит больше одной параллельной ей геодезической, неверно.
Первейшим понятием в геометрии является понятие пространства. Модернистская теория в математике утверждает существование неевклидова пространства.
В модернистской теории пространство определяется сначала как векторное, затем как метрическое, затем как топологическое, но все эти определения оказываются условными, не несущими первичного геометрического смысла (Def. 1.0.). Б.А. Розенфельд в капитальном труде «Неевклидовы геометрии» пишет (стр. 12): «Трехмерное евклидово пространство R₃ можно определить как множество, состоящее из элементов двух родов – точек и векторов, удовлетворяющих четырем группам аксиом». Далее, размерность пространства определяется через понятие линейной комбинации векторов: «Векторы  линейно независимы, если их линейная комбинация , при том, что все числовые коэффициенты ». «Аксиома размерности: существуют 3 линейно независимых вектора, но всякие 4 вектора линейно зависимы». Далее, «метрическим пространством называется множество элементов, называемых точками, для каждых двух из которых определено вещественное число ρ(x,y), называемое расстоянием». «Взаимно однозначное соответствие между точками двух метрических пространств, при котором расстояния между соответственными точками равны, называется изометрическим соответствием, а два метрических пространства, между которыми можно установить изометрическое соответствие, называются изометрическими пространсвами». «Топологическим пространством называется множество элементов, в котором выделена система подмножеств, называемых замкнутыми множествами, удовлетворяющими аксиомам…».
Обсуждение: Пространство в этой теории определяется как множество элементов, удовлетворяющих группе аксиом. Это определение изначально не соответствует понятию геометрического пространства (Def. 1.0.). «Множество элементов» есть множество элементов, или просто множество; такое определение пространства является условным, алгебраическим, не несущим геометрического смысла этого понятия. Пространство является не compositum, а totum; пространство как целостность не складывается из частей, напротив, его части могут быть выделены из целого.
Из определения пространства как множества элементов делается вывод о существовании множества пространств – в нарушение понятия пространства и в геометрии, и в естественных науках, и в философии как единственного; в алгебре может существовать ряд множеств, геометрическое пространство – одно.
Далее, элементы множества в этой теории не несут геометрического смысла, что дает возможность использовать в качестве «элементов пространства» любые алгебраические элементы, удовлетворяющие группе аксиом, также не несущих специфики геометрии, а выражающих алгебраические свойства ассоциативности, коммутативности, дистрибутивности.
Если сначала при определении векторного пространства вектор понимается в геометрическом смысле, то затем под вектором понимается алгебраический объект, удовлетворяющий указанным выше аксиомам, а под скалярным произведением понимается алгебраическое соотношение между этими объектами, ставящее в соответствие им некоторое число. В качетсве примеров векторных пространств приводятся: множество матриц заданного типа, совокупность всех непрерывных функций на заданном отрезке, совокупность всех многочленов, то есть объекты алгебры, а это означает, что введенные определения не соответствуют специфике геометрии. Таким образом модернистская теория является не обобщением в геометрии, а подменой геометрии алгеброй.
Что касается групп аксиом, то Розенфельд утверждает следующее (стр. 33): «Важным требованием, предъявляемым к системе аксиом, является независимость аксиом друг от друга». Это высказывание внутренне противоречиво: если аксиомы составляют систему, то это означает по определению, что они находятся в связях друг с другом. Иначе и быть не может: аксиомы составляют систему утверждений, так как образуют логические связи, в силу чего возможно выдвижение теоремы и построение ее доказательства на основе аксиом. Другое дело, что аксиомы не должны дублировать доказываемую теорему, но это не означает требования их независимости друг от друга.
Одним из важнейших научных вопросов является вопрос о мерности пространства. В модернистской теории мерность векторного пространства определяется числом линейно независимых векторов. Розенфельд пишет (стр. 37): «N-мерное евклидово пространство  есть множество элементов двух родов – точек и векторов, удовлетворяющих тем же аксиомам, что и пространство , но вместо аксиомы размерности  удовлетворяющее аксиоме: существуют n линейно независимых векторов, но всякие n+1 векторов линейно зависимы». Векторы разлагаются по ортогональному базису пространства, то есть представляются как линейная комбинация базисных векторов; ортогональность базиса в этой теории определяется через равенство нулю скалярного произведения пары векторов. Далее осуществляется переход к так называемому неевклидову пространству. Розенфельд (стр. 150) определяет n-мерное неевклидово пространство как множество элементов, называемых точками, находящихся во взаимно однозначном и изометрическом соответствии с парами диаметрально противоположных точек гиперсферы в пространстве . То есть переход от n-мерного евклидова пространства к n-мерному неевклидову пространству осуществляется путем отождествления двух диаметрально противоположных точек гиперсферы, которые принимаются за одну точку нового пространства. Это слишком большое допущение для сохранения единства теории.
Введенное в этой теории определение мерности пространства неверно. Линейная комбинация векторов допускает произвольный выбор числовых коэффициентов. Если рассмотреть два противоположно направленных вектора  и , то просто сумма их есть нулевой вектор: , то есть векторы линейно зависимы. Но если для вектора  выбрать другой числовой коэффициент, например, 2, то линейная комбинация этих же векторов будет ненулевым вектором: . Розенфельд уточняет, что нулевому вектору должна быть равна хотя бы одна линейная комбинация линейно зависимых векторов. Три вектора могут быть линейно зависимыми. Например, векторы , , , если ; линейная комбинация этих векторов с числовыми коэффициентами, равными единице, то есть просто сумма, есть нулевой вектор: , то есть 3 вектора линейно зависимы. Четыре вектора могут быть линейно независимыми. Пусть даны некоторые векторы , , , . Найдем их сумму: если , то ; если , то ; если , то , то есть 4 вектора , , ,  линейно независимы. Равенство или неравенство нулевому вектору линейной комбинации векторов определяет не мерность пространства, а определяет, будет ли ломаная, образованная последовательностью данных векторов, замкнутой или нет.
Через любую точку пространства проходит бесконечно много прямых. Прямая задается вектором, значит, линейно независимых векторов может быть бесконечно много. Отсюда делается вывод о существовании n-мерного пространства. Это неверный вывод из неверного определения.
Пара векторов, равенство нулю скалярного произведения которых принимается за определение их ортогональности, не определяет базис пространства, так как не соответствует мерности геометрического пространства, равной числу независимых пространственных измерений в нем, которых – три.
Мерность пространства определяется числом векторов ортонормированного базиса. Ортогональность базисных векторов пространства определяется геометрически и для всех сразу – следующим образом: двойное векторное произведение базисных векторов есть нулевой вектор, а модуль каждого равен единице, что может определяться как равенство единице скалярного произведения каждого базисного вектора на себя (так как скалярный квадрат вектора равен квадрату его модуля):
 или ,
при этом в двойном векторном произведении возможна циклическая перестановка векторов, а всего их может быть только три. Трехмерность – фундаментальное свойство пространства.
В модернистской теории «пространство» понимается неоднозначно, например, «прямые линии евклидова пространства  называют одномерными евклидовыми пространствами » (Розенфельд, стр. 19), то есть термин «пространство» здесь – чисто условный, прилагающийся к разным объектам, что является нарушением логического закона тождества.
Чтобы не нарушался логический закон тождества и сохранялась система дефиниций, нужно, чтобы соблюдался принцип занятости понятия: если некоторое понятие поставлено в соответствие некоторому объекту путем дефиниции последнего, то это понятие не может и не должно ставиться в соответствие никакому другому объекту.
Введение n-мерного пространства вместо трехмерного является подменой геометрии алгеброй. Отождествление некоторой области пространства с пространством как таковым нарушает логический закон тождества. Следующая за таким отождествлением интерпретация кривизны поверхности, ограничивающей рассматриваемую область пространства, как кривизны пространства и объявление его неевклидовым оказывается следствием нарушения логического закона тождества и не имеет достаточных оснований. Более того, такая интерпретация противоречит основным свойствам пространства – бесконечности, однородности, изотропности, являющимися главным условием введения метода координат, на котором основана почти вся математика. Поэтому попытки представить геометрию прямых и плоскостей как предельный случай геометрии кривых линий и криволинейных поверхностей методологически неверны; они подрывают основы аналитической геометрии. Кривая или поверхность задаются аналитически и тем самым идентифицируются, а это значит, что геометрия прямых, в которой вводится координатный метод, первична по отношению к геометрии кривых.
Рассматривать геометрию прямых как частный, предельный случай геометрии кривых неправомерно еще по одной причине. Как прямая делит плоскость на две полуплоскости, так и плоская кривая делит плоскость на две, вообще говоря, неравные части, так, что: отрезок, соединяющий любые две точки разных частей плоскости, образованных кривой, пересекает эту кривую нечетное число раз, а отрезок, соединяющий любые две точки одной части плоскости, либо не пересекает эту кривую, либо пересекает ее четное число раз. Аналогично криволинейная поверхность делит пространство на две неравные области – с тем же правилом пересечения отрезками поверхности, что справедливо для кривой. Поверхности, вообще говоря, являются двусторонними (лист Мебиуса – особый случай). В зависимости от того, из какой области пространства ведется рассмотрение криволинейной поверхности, она является одновременно поверхностью или положительной, или отрицательной кривизны. Если относительно одной области пространства эта поверхность является поверхностью положительной кривизны, то есть выпуклой, то относительно другой области пространства эта же поверхность на том же своем участке является поверхностью отрицательной кривизны, то есть вогнутой (например, при рассмотрении сферы из внешней по отношению к ней области она оказывается выпуклой поверхностью, при рассмотрении же ее из внутренней области она оказывается вогнутой поверхностью). Следовательно, знак кривизны, определяющий характер кривизны поверхности – выпуклость или вогнутость, оказывается относительной величиной, тогда как прямолинейность абсолютна.
Вывод. Существуют геометрия прямых и плоскостей и геометрия кривых и криволинейных поверхностей (а не «евклидова геометрия» и «неевклидова геометрия»); геометрия кривых закономерно отличается от геометрии прямых, но при этом основывается на ней; кривая и поверхность задаются аналитически, что означает первичность геометрии прямых как основы метода координат.

Пространство первично по отношению к любым геометрическим объектам – элементам, фигурам, телам. Есть геометрические элементы, которые считаются основными; в планиметрии – это точки и прямые, в стереометрии – плоскости. Некоторые фигуры на плоскости и тела в пространстве в классической геометрии определяются как множество точек, удовлетворяющих некоторым заданным условиям. Такие определения требуют уточнения.
Множество точек, являющихся нульмерными объектами, не может дать одномерность. Сумма нулей равна нулю. Точка, будучи нульмерным объектом, является границей одномерного объекта. Таким одномерным объектом является элементарная длина – основной объект дифференциальной геометрии.
Если пространственная кривая задана уравнениями: , , где  – гладкие функции на отрезке значений аргумента , то длина соответствующего участка кривой равна:
,
то есть определяется интегралом от элементарной длины. Аналогично, если кривая задана в пространстве параметрически: , , , где , то длина участка кривой, соответствующая монотонному изменению параметра в указанных пределах, вычисляется по формуле:
,
представляющей собой интеграл от элементарной длины.
Эти интегралы получаются в результате следующего приближения. Если в интервале  выбрать n промежуточных точек, то кривая разобьется на n частей. В заданную кривую вписывается ломаная, состоящая из n звеньев. Длина ломаной, вписанной в кривую, при бесконечном измельчении разбиения стремится к пределу, называемому длиной участка кривой.
Аналогично площадь S ограниченной регулярной поверхности σ определяется следующим образом: σ разбивается на конечное число частей; в каждой части поверхности выбирается произвольная точка, и каждая часть ортогонально проецируется на касательную плоскость к поверхности в выбранной точке. Площадь поверхности S есть предел суммы площадей проекций, когда диаметр наибольшей из рассматриваемых частей стремится к нулю:
.
Таким образом, линия на плоскости или в пространстве должна определяться как множество элементарных длин. Точки принадлежат этой линии как границы элементарных длин, из которых она складывается. Фигура и геометрический элемент на плоскости должны определяться как множество элементарных длин (а не точек). Точки принадлежат фигуре как границы элементарных длин, множеством которых являются линии, образующие фигуру. Плоская фигура и фигура на поверхности должны определяться как множество элементарных площадей. Точки принадлежат этой фигуре как границы элементарных линий, ограничивающих каждую элементарную площадь. Таким образом, элементарная длина выступает базовым геометрическим элементом.
Обычные в классической геометрии представления, как-то: «точка лежит на прямой», «точка лежит на кривой», «расстояние между двумя точками» и другие остаются в силе; при этом нужно понимать, что рассматриваемые объекты образованы не множеством точек, а множеством элементарных длин, границами которых являются точки. «Расстояние между двумя точками» есть расстояние между началом первой из элементарных длин и концом последней на рассматриваемом участке линии.
Прямая тоже слагается из элементарных длин. Прямая на плоскости задается аналитически – уравнениями разного вида:
уравнением прямой, проходящей через две данные точки плоскости  и : ;
уравнением с угловым коэффициентом и начальной ординатой: , где , , что следует из предыдущего уравнения;
уравнением прямой в общем виде, которое может быть представлено в форме, совмещающей уравнение с координатами двух точек и уравнение с угловым коэффициентом, в силу чего оно может быть названо универсальным: .
Длина прямой на плоскости между двумя точками  и  рассчитывается по общей формуле: , то есть складывается из элементарных длин.
,
где  – модуль вектора, соединяющего точки  и , который является разностью радиус-векторов этих точек. Модуль вектора  по определению является расстоянием между точками  и . Из приведенного расчета следует, что длина прямой между двумя точками равна расстоянию между этими точками, что доказывается с помощью дифференциальной геометрии. Именно так определяется прямая в классической геометрии (Def. 1.7.). Это свойство прямой обусловливает использование прямой в качестве оси координат, то есть лежит в основе координатного метода.
Вывод. Помимо точек и прямых, считающихся основными элементами в планиметрии, к основным геометрическим элементам должны быть отнесены элементарные длины, являющиеся базовыми одномерными объектами. Точки как нульмерные объекты не существуют сами по себе, а являются границами элементарных длин. Множества элементарных длин образуют линии, в том числе и прямые. Таким образом элементарные длины выступают основными элементами при построении фигур.

Библиографический список

1. Энциклопедия элементарной математики. Книга четвертая. Геометрия. – М.: Гос. изд-во физико-математической литературы, 1963. – 568 с.
2. Погорелов А.В. Геометрия. Учебное пособие для 6-10 классов средней школы. – М.: Просвещение, 1980. – 288 с.
3. Точка (геометрия) // Материал из Википедии – свободной энциклопедии. URL: https://ru.wikipedia.org/wiki/%D0%A2%D0%BE%D1%87%D0%BA%D0%B0.. (дата обращения: 13.10.2018).
4. «Начала» Евклида. Книги I-VI. – М.-Л.: ОГИЗ, Гос. изд-во технико-теоретической литературы, 1948. – 447 с. – (Классики естествознания).
5. Аксиома параллельности Евклида // Материал из Википедии – свободной энциклопедии. URL: https://ru.wikipedia.org/wiki/%D0%90%D0%BA%D1%81%D0%B8%D0%BE%D0.. (дата обращения: 3.09.2018).
6. Аргунов Б.И., Бланк М.Д. Геометрические построения на плоскости. – М.: Гос. учебно-педагогическое изд-во Мин. просвещения РСФСР, 1957. – 267 с.
7. Выгодский М.Я. Справочник по элементарной математике. – М.-Л.: Гос. изд-во технико-теоретической лит-ры, 1950. – С. 274.
8. Таблица математических символов // Материал из Википедии – свободной энциклопедии. URL: https://ru.wikipedia.org/w/index.php?title=Таблица_математических_символов&oldid=98096487 (дата обращения: 13.02.2019).
9. Игошин В.И. Математическая логика: Учебное пособие. – М.: ИНФРА-М, 2016. – 399 с. – (Высшее образование).
10. Лобачевский Н.И. Геометрические исследования по теории параллельных линий. – М.-Л.: Изд-во Академии наук СССР, 1945. – 177 с.
11. Лобачевский Н.И. Избранные труды по геометрии. – М.: Изд-во АН СССР, 1956. – 596 с. – (Классики науки).
12. Новоселов М.М., Курбатов В.И., Бернштейн В.С. Законы логики // Гуманитарные технологии. Аналитический портал [Электронный ресурс]. URL: https://gtmarket.ru/concepts/6922 (дата обращения 23.04.2019).
13. Погорелов А.В. Основания геометрии. – М.: Наука. Гл. ред. физ.-мат. лит., 1979. – 152 с.
14. Геометрия Лобачевского // Материал из Википедии – свободной энциклопедии. URL: https://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1.. (дата обращения 8.10.2018).
15. Выгодский М.Я. Справочник по высшей математике. – М.: Наука. Гл. ред. физ.-мат. лит., 1977. – 872 с.
16. Михалев А.А., Михалева Т.Б. Сферическая геометрия. – Кемерово: Институт фундаментальных наук КемГУ, 2016. – 18 с.
17. Бельтрами Э. Опыт интерпретации неевклидовой геометрии. – В кн.: Основания геометрии. / Сб. под ред. А.П. Нордена. – М.: Гос. изд-во технико-теоретической лит-ры , 1956. – 528 с.
18. Розенфельд Б.А. Неевклидовы геометрии. – М.: Гос. изд-во технико-теоретической литературы, 1955. – 744 с.
19. Канатников А.Н., Крищенко А.П. Аналитическая геометрия: Конспект лекций. – М.: МГТУ им. Баумана, 2009. – 45 с.
20. Рашевский П.К. Курс дифференциальной геометрии. – М., Л.: Гос. изд-во технико-теоретической литературы, 1950. – 428 с.
21. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). – М.: Наука. Гл. ред. физ.-мат. лит., 1973. – 832 с.

---

Количество просмотров публикации: Please wait

Все статьи автора «Плисова Ника Николаевна»