Введение. Работа посвящена вопросам анализа интегрированных проектов на эффективность и является продолжением исследований, опубликованных в [1], [2]. Ниже использованы основные понятия, обозначения и методики, рассмотренные в этих работах. Рассмотрен новый подход к оцениванию доходностей интегрированных проектов (ИП) в целом и частных проектов, входящих в них. Рассмотрен иллюстративный пример. Предложены задачи оптимизации параметров интегрированных проектов.
Новый подход к оцениванию доходности ИП и его использование в задачах анализа проектов на эффективность. Итак, предположим, что при оценивании дохода проекта на основе метода детализации финансовых потоков была использована формула ![]() (см. подробнее [1], [2]). Таким образом, доход ИП был оценен теми финансовыми средствами, которые были аккумулированы проектами из множества Pr6 на момент времени
(см. подробнее [1], [2]). Таким образом, доход ИП был оценен теми финансовыми средствами, которые были аккумулированы проектами из множества Pr6 на момент времени ![]() .
.
Рассмотрим новый подход (отличный от рассмотренных ранее, см., например, [5], [6], [7]) к оцениванию доходности ИП и частных проектов множества Pri=![]() . Он основан на простой идее, которая состоит в том, что в доход ИП
. Он основан на простой идее, которая состоит в том, что в доход ИП ![]() свой вклад вносят не элементы входных потоков
свой вклад вносят не элементы входных потоков ![]() ,
, ![]() , а только их части –
, а только их части – ![]() , где
, где ![]() – искомая доходность ИП. Эта идея может быть реализована в виде следующего формального выражения:
– искомая доходность ИП. Эта идея может быть реализована в виде следующего формального выражения:
![]() .
.
Затем, как это было предложено ранее (см. [1], [2]), можно оценить доходы каждого из частных проектов, используя эту оценку для доходности ИП. Предположим, что доходы для частных проектов были найдены и они равны ![]() ,
, ![]()
![]() . Тогда можно оценить доходности каждого из частных проектов. Для этого можно воспользоваться следующими расчетными формулами:
. Тогда можно оценить доходности каждого из частных проектов. Для этого можно воспользоваться следующими расчетными формулами:
![]() ,
, ![]()
![]() .
.
Рассмотрим пример анализа ИП на эффективность с использованием новой методики. Пусть заданы два частных проекта (![]() Pr1 и
Pr1 и ![]() Pr4) своими финансовыми потоками (см. Табл. 1 и Табл. 2). Необходимо оценить эффективность частных проектов до начала интеграционного процесса, эффективность интегрированного проекта и эффективности каждого из частных проектов в рамках интегрированного проекта, сделать вывод о целесообразности интеграции. Отметим особенности частных проектов
Pr4) своими финансовыми потоками (см. Табл. 1 и Табл. 2). Необходимо оценить эффективность частных проектов до начала интеграционного процесса, эффективность интегрированного проекта и эффективности каждого из частных проектов в рамках интегрированного проекта, сделать вывод о целесообразности интеграции. Отметим особенности частных проектов ![]() и
и ![]() на основании анализа их потоков. Проект
на основании анализа их потоков. Проект ![]() находится на стадии снижения своей активности. Его доход со временем уменьшается, падает рентабельность. Проект
находится на стадии снижения своей активности. Его доход со временем уменьшается, падает рентабельность. Проект ![]() является новым, он требует инвестиций для своей реализации, его доход и рентабельность со временем увеличиваются.
является новым, он требует инвестиций для своей реализации, его доход и рентабельность со временем увеличиваются.
|
70
|
50
|
50
|
40
|
30
|
|
|
100
|
|
|
|
|
|
|
50
|
50
|
60
|
70
|
70
|
|
|
0
|
|
|
|
|
Итак, требуется решить три подзадачи по оцениванию эффективности: оценить эффективность проекта ![]() , оценить эффективность проекта
, оценить эффективность проекта ![]() и, наконец, оценить эффективность ИП из двух проектов –
и, наконец, оценить эффективность ИП из двух проектов – ![]() и
и ![]() . Для решения этих задач воспользуемся методиками и алгоритмами, рассмотренными в [1], [2].
. Для решения этих задач воспользуемся методиками и алгоритмами, рассмотренными в [1], [2].
Оценивание эффективности проекта ![]() .
.
Для ![]() находим
находим ![]() ден. ед. и
ден. ед. и ![]() ден. ед. Для ставки
ден. ед. Для ставки ![]() получим
получим ![]() ден. ед.
ден. ед.
Для ![]() находим
находим ![]() ден. ед. Для ставки
ден. ед. Для ставки ![]() вычислим
вычислим ![]() ден. ед.
ден. ед.
Для ![]() находим
находим ![]() ден. ед. Для ставки
ден. ед. Для ставки ![]() получим
получим ![]() ден. ед.
ден. ед.
Для ![]() и для ставки
и для ставки ![]() находим
находим ![]() ден. ед.
ден. ед.
Наконец, для ![]() находим
находим ![]() ден. ед.
ден. ед.
Таким образом, можно заключить, что доход проекта ![]() равен
равен ![]() ден. ед. Найдем доходность проекта
ден. ед. Найдем доходность проекта ![]() . Для этого воспользуемся формулой:
. Для этого воспользуемся формулой:
![]()
=![]() .
.
Получим ![]() 0.28071 (или 28.071%).
0.28071 (или 28.071%).
Оценивание эффективности проекта ![]() .
.
Для ![]() находим
находим ![]() 50 ден. ед.,
50 ден. ед., ![]()
![]() . Для
. Для ![]() 4,
4, ![]() ,
, ![]() 0.1 получим
0.1 получим ![]() ден. ед.,
ден. ед., ![]() .
.
Для ![]() находим
находим ![]()
![]() ден. ед.,
ден. ед., ![]()
![]() . Для
. Для ![]() 4,
4, ![]() ,
, ![]() 0.1 вычислим
0.1 вычислим ![]() ден. ед.,
ден. ед., ![]() .
.
Для ![]() находим
находим ![]() ден. ед. Для ставки
ден. ед. Для ставки ![]() получим
получим ![]() ден. ед.
ден. ед.
Для ![]() находим
находим ![]() ден. ед. Для ставки
ден. ед. Для ставки ![]() получим
получим ![]() ден. ед.
ден. ед.
Наконец, для ![]() находим
находим ![]() ден. ед.
ден. ед.
Тогда, можно заключить, что доход проекта ![]() равен
равен ![]() ден. ед. Найдем доходность проекта
ден. ед. Найдем доходность проекта ![]() . Для этого воспользуемся формулой:
. Для этого воспользуемся формулой:
![]()
=![]() .
.
Получим ![]() 0.11989 (или 11.989 %).
0.11989 (или 11.989 %).
Оценивание эффективности ИП проекта, включающего в себя проекты ![]() и
и ![]() .
.
Для ![]() находим
находим ![]() 20 ден. ед.,
20 ден. ед., ![]()
![]() . Для
. Для ![]() 4,
4, ![]() ,
, ![]() 0.1 получим
0.1 получим ![]() ден. ед.,
ден. ед., ![]() .
.
Для ![]() находим
находим ![]() 36.309 ден. ед.,
36.309 ден. ед., ![]()
![]() . Для
. Для ![]() 4,
4, ![]() ,
, ![]() 0.1 получим
0.1 получим ![]() ден. ед.,
ден. ед., ![]() .
.
Для ![]() и для ставки
и для ставки ![]() находим
находим ![]() ден. ед.
ден. ед.
Для ![]() и для ставки
и для ставки ![]() находим
находим ![]() ден. ед.
ден. ед.
Для ![]() находим
находим ![]() ден. ед.
ден. ед.
Таким образом, доход ИП равен ![]() ден. ед. Найдем доходность проекта ИП. Для этого воспользуемся формулой:
ден. ед. Найдем доходность проекта ИП. Для этого воспользуемся формулой:
![]()
=![]() .
.
Получим ![]() 0.1837 (или 18.37 %).
0.1837 (или 18.37 %).
Найдем доходы в общем доходе ИП ![]() ден. ед., приходящиеся на каждый из частных проектов
ден. ед., приходящиеся на каждый из частных проектов ![]() и
и ![]() . Получим
. Получим
![]() ден. ед. и
ден. ед. и
![]() ден. ед.
ден. ед.
А затем найдем
![]() (или 46.80 % от общего дохода ИП) и
(или 46.80 % от общего дохода ИП) и
![]() ден. ед. (или 53.20 % от общего дохода ИП).
ден. ед. (или 53.20 % от общего дохода ИП).
Сведем результаты моделирования в общую таблицу (см. Табл. 3).
|
Проекты
|
Доход
|
Доходность
|
| Проект |
|
28.071
|
| Проект |
|
11.989
|
| Интегрированный проект |
|
18.37
|
| Проект |
|
18.37
|
| Проект |
|
18.37
|
Сделаем некоторые выводы на основании проделанных вычислений.
Заметим, что доход и доходность самостоятельных проектов ![]() и
и ![]() по сравнению с этими же показателями этих проектов в рамках ИП
по сравнению с этими же показателями этих проектов в рамках ИП ![]() очевидным образом уменьшились и увеличились для первого и второго проектов соответственно.
очевидным образом уменьшились и увеличились для первого и второго проектов соответственно.
Доход и доходность ИП ![]() были бы выше, если бы были учтены возможные свободные финансовые средства проекта
были бы выше, если бы были учтены возможные свободные финансовые средства проекта ![]() , которые он заработал до момента времени
, которые он заработал до момента времени ![]() .
.
Можно предположить, что интеграция выгодна только для проекта ![]() . Однако, при увеличении правой границы временного интервала
. Однако, при увеличении правой границы временного интервала ![]() , на котором анализируется ИП, картина может существенно измениться. ИП
, на котором анализируется ИП, картина может существенно измениться. ИП ![]() может стать выгодным (интересным) проекту
может стать выгодным (интересным) проекту ![]() , поскольку он завершает свой жизненный цикл.
, поскольку он завершает свой жизненный цикл.
Оптимизация ИП. Определим множества параметров проектов ![]() ,
, ![]() следующим образом:
следующим образом:![]() для проектов
для проектов ![]() ,
, ![]() , времена
, времена ![]() и
и ![]() ,
, ![]() , – это не времена начала и окончания соответствующих проектов, а времена начала и окончания участия их в анализируемом ИП на интервале
, – это не времена начала и окончания соответствующих проектов, а времена начала и окончания участия их в анализируемом ИП на интервале ![]() ;
; ![]() для проектов
для проектов ![]() ,
, ![]() ;
; ![]() для проектов
для проектов ![]() ,
, ![]() . Напомним, обозначения
. Напомним, обозначения ![]() – времена начала и окончания жизни проектов
– времена начала и окончания жизни проектов ![]() ,
, ![]() ,
, ![]() и
и ![]() – начало и конец жизненного цикла проекта
– начало и конец жизненного цикла проекта ![]() ,
, ![]() (время получения заемных средств и окончания расчета за них соответственно);
(время получения заемных средств и окончания расчета за них соответственно);![]() (или
(или ![]() ) – число выплат по заемным средствам проектов
) – число выплат по заемным средствам проектов ![]() ,
, ![]() ;
; ![]() (или
(или ![]() ) – ставка заимствования для проектов
) – ставка заимствования для проектов ![]() ,
, ![]() ;
; ![]() и
и ![]() – времена начала и окончания жизненного цикла проектов
– времена начала и окончания жизненного цикла проектов ![]() ,
, ![]() ;
; ![]() (или
(или ![]() ) – ставка внешнего использования средств проекта.
) – ставка внешнего использования средств проекта.
Сведем параметры всех проектов ![]() ,
, ![]() в один общий вектор и обозначим его через
в один общий вектор и обозначим его через ![]() . Тогда, если Q – показатель эффективности проекта
. Тогда, если Q – показатель эффективности проекта ![]() (например, доход, доходность, срок окупаемости проекта), то задача оптимизации этого проекта может быть представлена следующим образом:
(например, доход, доходность, срок окупаемости проекта), то задача оптимизации этого проекта может быть представлена следующим образом:
![]()
Здесь задача на экстремум сводится к нахождению минимума или максимума критерия ![]() в зависимости от его значения. Так, например, при
в зависимости от его значения. Так, например, при ![]() или
или ![]() оптимизационная задача будет задачей по нахождению максимальных значений этих критериев на множестве допустимых значений параметров
оптимизационная задача будет задачей по нахождению максимальных значений этих критериев на множестве допустимых значений параметров ![]() . А при
. А при ![]() (срок окупаемости проекта, критерий можно было бы обозначить и как
(срок окупаемости проекта, критерий можно было бы обозначить и как ![]() , подчеркивая индексом, что показатель относится к ИП) будет решаться задача на минимум.
, подчеркивая индексом, что показатель относится к ИП) будет решаться задача на минимум.
В случае векторного критерия ![]() задача поиска наилучшего сочетания параметров ИП будет выглядеть следующим образом:
задача поиска наилучшего сочетания параметров ИП будет выглядеть следующим образом:
![]()
При использовании для решения этой задачи, например, метода главного критерия, она сведется к следующей однокритериальной задаче:
![]()
при ограничениях
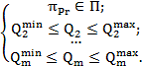
Заметим, что использование для решения многокритериальной задачи метода нормализации критериев не представляется возможным, поскольку этот метод является неустойчивым относительно пассивных ограничений задачи (подробнее об этом свойстве метода нормализации критериев см., например, в работах [6], [15], [16]).
Следует обратить внимание на то обстоятельство, что оптимизируя ИП по параметрам ![]() , введенным в рассмотрение выше, может быть нарушена связь этих параметров с потоками ИП. Другими словами, изменяя в ИП такие параметры как, например, сроки реализации проекта могут измениться такие характеристики ИП, как объемы входных и выходных финансовых потоков (объемы инвестиций и доходов). Поэтому представляется более логичным проводить оптимизацию ИП по множеству характеристик частных проектов: по множеству характеристик потоковых моделей соответствующих им процессных моделей (бизнес-процессов) (см., например, [3], [4], [9]).
, введенным в рассмотрение выше, может быть нарушена связь этих параметров с потоками ИП. Другими словами, изменяя в ИП такие параметры как, например, сроки реализации проекта могут измениться такие характеристики ИП, как объемы входных и выходных финансовых потоков (объемы инвестиций и доходов). Поэтому представляется более логичным проводить оптимизацию ИП по множеству характеристик частных проектов: по множеству характеристик потоковых моделей соответствующих им процессных моделей (бизнес-процессов) (см., например, [3], [4], [9]).
Наполним содержанием финансовые потоки ИП с целью исследовать задачи оптимизации и управления этими проектами. Первоначально это сделаем так, как это предложено, например, в работах [17], [18] и в некоторых других, а затем введем некоторые изменения и уточнения в формальном представлении этих потоков.
Итак, введем обозначения [17]. Пусть ![]() – рентабельность затрат (
– рентабельность затрат (![]() – операционный доход);
– операционный доход); ![]() – «шумпетерианская» рента (
– «шумпетерианская» рента (![]() – рентный доход);
– рентный доход); ![]() – переменные затраты на одну единицу выпуска изделия;
– переменные затраты на одну единицу выпуска изделия; ![]() – предполагаемый объем выпуска продукции;
– предполагаемый объем выпуска продукции; ![]() – часть постоянных затрат, приходящихся на изделия;
– часть постоянных затрат, приходящихся на изделия; ![]() – ставка налога на прибыль для предприятия.
– ставка налога на прибыль для предприятия.
Тогда прибыль может быть оценена следующим образом [17]:
![]() .
.
Преобразуем это выражение:
![]()
![]()
![]() ,
,
![]() .
.
Для множества проектов Pri =![]() можем представить входные и выходные потоки в виде:
можем представить входные и выходные потоки в виде:
![]() , (1)
, (1)
![]() ,
, ![]() ;
; ![]() ,
,
и
![]()
![]() (2)
(2)
![]() ,
, ![]() ;
; ![]() .
.
Отметим особенности потоков проектов множеств Pri, ![]() . Для проектов из множества Pr1 (продолжающихся на интервале
. Для проектов из множества Pr1 (продолжающихся на интервале ![]() проектов) потоки будут иметь вид (1) и (2).
проектов) потоки будут иметь вид (1) и (2).
Для проектов из множества Pr2 (завершающихся на интервале ![]() проектов) потоки могут иметь нулевые значения, начиная с моментов времени
проектов) потоки могут иметь нулевые значения, начиная с моментов времени ![]() ,
, ![]() , т.е.
, т.е.
![]() (3)
(3)
![]() ,
, ![]() ,
,
и
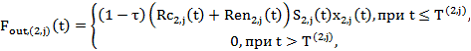 (4)
(4)
![]() ,
, ![]() .
.
Для проектов из множества Pr3 (приходящих на смену проектам из множества Pr2 на интервале ![]() ) потоки могут иметь нулевые значения, начиная с момента времени
) потоки могут иметь нулевые значения, начиная с момента времени ![]() , и до начала проведения НИОКР. Время окончания НИОКР –
, и до начала проведения НИОКР. Время окончания НИОКР – ![]()
![]() ,
, ![]() . А начиная с момента
. А начиная с момента ![]() , формируется выходной поток проекта (поток доходов). Таким образом, для этих проектов
, формируется выходной поток проекта (поток доходов). Таким образом, для этих проектов
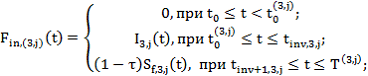 (5)
(5)
![]() ,
, ![]() ,
,
и
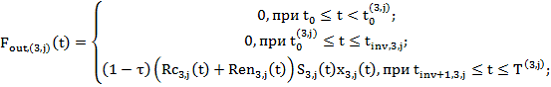 (6)
(6)
![]() ,
, ![]() . Здесь
. Здесь ![]() – инвестиции в проект
– инвестиции в проект ![]() ,
, ![]() , в момент времени
, в момент времени ![]() . Элементы потоков (5) и (6) равны нулю для всех
. Элементы потоков (5) и (6) равны нулю для всех ![]() ,
, ![]() . Заметим, что проекты из множеств Pr2 и Pr3образуют пары («выбывающий–замещающий») и их характеристики и параметры должны быть согласованы.
. Заметим, что проекты из множеств Pr2 и Pr3образуют пары («выбывающий–замещающий») и их характеристики и параметры должны быть согласованы.
Наконец, для проектов из множества Pr4 (новые, инновационные) входные и выходные потоки имеют вид аналогичный виду этих потоков для проектов из Pr3.
Заметим, что интервалы времени ![]() ,
, ![]() , включают в себя в качестве подинтервалов моменты времени, относящиеся ко всем стадиям НИОКР (фундаментальное исследование, прикладное исследование, разработка конструкторско-технологической документации, создание опытного образца, производство опытной партии, маркетинг, запуск массового производства). Аналогично обстоит дело и для проектов из Pr4.
, включают в себя в качестве подинтервалов моменты времени, относящиеся ко всем стадиям НИОКР (фундаментальное исследование, прикладное исследование, разработка конструкторско-технологической документации, создание опытного образца, производство опытной партии, маркетинг, запуск массового производства). Аналогично обстоит дело и для проектов из Pr4.
С учетом введенных в рассмотрение детализаций элементов финансовых потоков, множества параметров проекта изменятся и могут быть, представлены, например, в виде:
- для проектов ![]() ,
, ![]() , – это параметры
, – это параметры ![]() . Здесь
. Здесь ![]() и
и ![]() ,
, ![]() , – это времена начала и окончания участия их в анализируемом ИП на интервале
, – это времена начала и окончания участия их в анализируемом ИП на интервале ![]() ;
; ![]() – переменные затраты на одну единицу выпуска изделия; и
– переменные затраты на одну единицу выпуска изделия; и ![]() – объем выпуска продукции;
– объем выпуска продукции;
- для проектов ![]() ,
, ![]() , – это параметры
, – это параметры ![]() . Здесь
. Здесь ![]() и
и ![]() ,
, ![]() , – это времена начала и окончания участия их в анализируемом ИП на интервале
, – это времена начала и окончания участия их в анализируемом ИП на интервале ![]() ;
; ![]() – переменные затраты на одну единицу выпуска изделия; и
– переменные затраты на одну единицу выпуска изделия; и ![]() – объем выпуска продукции;
– объем выпуска продукции; ![]() – время окончания жизненного цикла;
– время окончания жизненного цикла;
- для проектов ![]() ,
, ![]() , – это параметры
, – это параметры ![]() . Здесь
. Здесь ![]() и
и ![]() ,
, ![]() , – это времена начала и окончания участия их в анализируемом ИП на интервале
, – это времена начала и окончания участия их в анализируемом ИП на интервале ![]() ;
; ![]() – переменные затраты на одну единицу выпуска изделия; и
– переменные затраты на одну единицу выпуска изделия; и ![]() – объем выпуска продукции;
– объем выпуска продукции; ![]() – время окончания жизненного цикла;
– время окончания жизненного цикла;![]() – начало жизненного цикла;
– начало жизненного цикла; ![]() – инвестиции в проект;
– инвестиции в проект; ![]() – время окончания НИОКР;
– время окончания НИОКР;
- для проектов ![]() ,
, ![]() , – это параметры
, – это параметры ![]() . Здесь
. Здесь ![]() и
и ![]() ,
, ![]() , – это времена начала и окончания участия их в анализируемом ИП на интервале
, – это времена начала и окончания участия их в анализируемом ИП на интервале ![]() ;
; ![]() – переменные затраты на одну единицу выпуска изделия; и
– переменные затраты на одну единицу выпуска изделия; и ![]() – объем выпуска продукции;
– объем выпуска продукции; ![]() – время окончания жизненного цикла;
– время окончания жизненного цикла;![]() – начало жизненного цикла;
– начало жизненного цикла; ![]() – инвестиции в проект;
– инвестиции в проект; ![]() – время окончания НИОКР.
– время окончания НИОКР.
Напомним, что использование модели для оценивания инвестиций инновационных проектов в виде [17], [18]:
![]()
представляется нерациональным. Объяснить это обстоятельство можно тем, что основное внимание при исследовании инновационного проекта на эффективность и оценивании инвестиций в проект уделено моменту времени ![]() (времени возврата вложений, времени окупаемости проекта). Однако не менее важной является задача нахождения характеристик проекта, относящихся к разным моментам времени на интервале его жизненного цикла [14].
(времени возврата вложений, времени окупаемости проекта). Однако не менее важной является задача нахождения характеристик проекта, относящихся к разным моментам времени на интервале его жизненного цикла [14].
В работе Е.Е. Досужевой (Модели оценки коммерческой эффективности инновационно-инвестиционных проектов, Интернет-журнал «НАУКОВЕДЕНИЕ», Том 7, №3 (май-июнь 2015)) сделана попытка построить оптимизационные модели для инновационных проектов для различных схем их реализации и форм заимствования инвестиций. К сожалению, ни одна из оптимизационных задач, приведенных в этой работе, не лишена грубых ошибок. Некоторые из проблем таких моделей хорошо известны и подробно рассмотрены в работах [6], [10], [19]-[23] и других.
Основные проблемы этих оптимизационных моделей состоят в следующем.Использовано выражение для дисконтированного срока окупаемости проекта, которое является ошибочным (см., например, [6], [19], [22]);
Предлагается оптимизировать элементы входных и выходных потоков проектов, которые на самом деле являются зависимыми;
Вводятся в рассмотрение объемы собственных и заемных средств, но не учитывается, что они являются динамическими величинами (зависят от времени);
Некоторые из оптимизационных задач лишены экономического смысла;
Использованы показатели на основе чистого приведенного дохода, которые имеют противоречивый характер и алогизмы;
Используемый показатель чистого приведенного дохода отождествляется с доходом проекта на начало его реализации, но, фактически, доход будет получен гораздо позднее. Именно то значение дохода, которое будет получено в будущем, нас и должно интересовать. Внутренняя норма доходности, как это хорошо известно, показывает лишь граничное значение для доходности. И т.д.Цель этих замечаний – пояснить ситуацию с проблемами оптимизационных задач, предложенных в работах аналогичных анализируемой работе, и предостеречь теоретиков и практиков от их использования. Грубые ошибки математического и экономического характера, допущенные при построении оптимизационных задач, требуют доработки соответствующих моделей и проведения дополнительных исследований.
Библиографический список
- Наумов А.А., Наумова А.А. Оценивание эффективности интегрированных проектов на основе метода детализации финансовых потоков// Современные научные исследования и инновации. 2015. № 7 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/07/56645 (дата обращения: 31.07.2015).
- Наумов А.А., Наумова А.А. К оцениванию эффективности интегрированных проектов// Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/56856 (дата обращения: 25.08.2015).
- Наумов А.А., Бах С.А. Бизнес-процессы. Синтез, анализ, моделирование и оптимизация. Новосибирск, 2007.
- Наумов А.А., Максимов М.А. Управление экономическими системами. Процессный подход. Новосибирск, 2008.
- Наумов А.А. К задаче оценивания частных эффектов интегрированных бизнес-процессов// Финансовая аналитика: Проблемы и решения. 2012. № 46 (136). С. 41-48.
- Наумов А.А. Методы анализа и синтеза инвестиционных проектов. Эффективность, риски, управление. LAP LAMBERT Academic Publishing, 2013.
- Наумов А.А. К задаче управления кластерными образованиями// Финансовая аналитика: проблемы и решения. 2011. № 41 (83). С. 51-58.
- Наумов А.А., Клавсуц И.Л., Лямзин О.Л. Инновации. Теория, модели, методы управления. Новосибирск, 2010.
- Наумов А. А. Теоретические и прикладные вопросы моделирования бизнес-процессов. Модели, алгоритмы, программы. LAP LAMBERT Academic Publishing, 2012.
- Наумов А.А. Перераспределение общего дохода между участниками интегрированного проекта// Theoretical & Applied Science, Materials of the ISPC «Advances in techniques&technologies», 30.10.2013, Milan, Italy. 2013. № 10(6). С. 129-132.
- Наумов А.А. Оптимизация структуры заимствований и вложений доходов инвестиционного проекта// Theoretical & Applied Science, Materials of the ISPC «Advances in techniques&technologies», 30.10.2013, Milan, Italy. 2013. № 10(6). С. 133-136.
- Наумов А.А. Оценивание эффективности интегрированных проектов// Финансовая аналитика: проблемы и решения. 2014. № 8 (194). С. 36-43.
- Наумов А.А. Управление портфельными инвестициями. Эффективность, риски, оптимизация. LAP LAMBERT Academic Publishing, Saarbrucken, 2014.
- Наумов А.А., Наумова А.А. К моделированию финансовых потоков инновационных проектов// Современные научные исследования и инновации. 2015. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/06/55010 (дата обращения: 18.06.2015).
- Наумов А.А. К проблемам метода нормализации критериев в задачах векторной оптимизации// Theoretical&Applied Science, Materials of the ISPC «Theory and Practice», 30.08.2013, Munich, Germany. 2013. № 8 (4). С. 24-26.
- Наумов А.А. К Sp-неустойчивости метода нормализации критериев решения многокритериальных задач оптимизации// Theoretical&Applied Science, Materials of the ISPC «Results &Perspectives», 30.09.2013, Florence, Italy. 2013. № 9 (5). С. 14-16.
- Растова Ю.И., Межов С.И. Методические основы прогнозной оценки объема инвестирования в инновационные проекты// Вестник СПбГЭУ, Сер. Экономика. 2014. Вып. 2(69). С. 78-83.
- Титов В.В., Межов С.И. Модель формирования операционно-инновационной программы промышленного предприятия// Совершенствование институциональных механизмов управления в промышленных корпорациях/ Под. ред. В.В.Титова, В.Д. Марковой. Новосибирск. 2013. С. 232 – 239.
- Наумов А.А. К вопросу о точности оценки дисконтированного срока окупаемости инвестиционного проекта// Финансовая аналитика: проблемы и решения. 2013. № 44 (182). С. 25-28.
- Наумов А.А. К вопросу об упрощении двух задач оптимизации инвестиций// Финансовая аналитика: проблемы и решения. 2013. № 46 (184). С. 26-30.
- Наумов А.А. О проблемах некоторых классических методов анализа экономических систем и путях их разрешения// Theoretical & Applied Science, Materials of the ISPC «The results of scientific research in 2013», 30.12.2013, Neoplanta, Serbia. 2013. № 12(8). С. 112-114.
- Наумов А.А., Наумова А.А. О проблемах моделей Досужевой-Кириллова анализа инвестиционных проектов и путях их разрешения// ISJ Theoretical&Applied Science, Materials of the ISPC «Industry&Technology Europe», 30.05.2015, Lyon, France. 2015. № 5 (25). С. 110-118.
- Список трудов. [Электронный ресурс]. URL: https://sites.google.com/site/anatolynaumov2011/home/spisok-trudov-list-of-papers (Дата обращения 17.08.15).

В формуле для оценивания доходности проекта Pr4(1) у переменных должен быть индекс 4. Приносим свои извинения за опечатку.