Основные предложения по модификации проективной геометрии изложены в предыдущих публикациях [2, 3, 4, 5, 6, 7] . В этой статье будет рассмотрены варианты пересечений и параллельность нечетких прямых.

Параллельность двух нечетких прямых
Параллельность двух нечетких прямых изменяется от 0 до 1, она равна инцидентности [8] бесконечно удаленных точек этих прямых. Даны две собственные прямые  и  параллельность (Н) этих прямых будет равна:
 (1)
Где  - тангенс угла между осями нечетких прямых 

Пересечение нечетких прямых
Две не инцидентные нечеткие прямые пересекаются в одной нечеткой точке. Имеется три варианта пересечения нечетких прямых. Первый – одна из прямых собственная вторая несобственная. Второй – обе прямые собственные параллельные между собой. Третий – прямые собственные непараллельные между собой.
Пересечение неинцидентных собственной и не собственной прямых  и  происходит в несобственной точке собственной прямой . Где , 

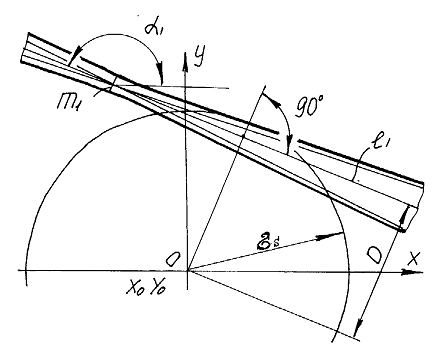
Рис.1. Определение инцидентности собственной и несобственной прямых

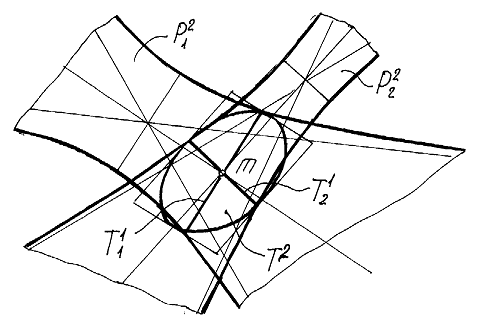
Рис. 2. Определение точки пересечения двух нечетких прямых

Если параллельность двух прямых  и  равна единице, то они имеют одну общую несобственную точку , которая является пересечением несобственных точек этих прямых. 
Где ,  
Даны две не параллельные не инцидентные прямые  и . 
Их точка пересечения  будет определяться (рис.1.) двумя одномерными нечеткими точками  и [3], которые являются перпендикулярными сечениями нечетких прямых в точке пересечения их осей. Уравнения осей имеют вид:
  
где , 
Точка их пересечения будет иметь координаты
 (2)
 (3)
Средние квадратичные отклонения одномерных точек соответствующих перпендикулярным сечениям прямых в их точке пересечения равны:
, (4) 
, (5)
где  - расстояния от точки пересечения до центра соответствующей прямой.
 (6) 
 (7)
Предложения по модификации проективной геометрии позволили разработать ряд приложений к AutoCAD позволяющих реконструировать размеры зданий по фотографиям [1]. 
Работа выполняется при финансовой поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности.

1. Косенков А. Ю., Марков Б. Г., Марков О. Б. Графическая реконструкция часовни Иконы Смоленской божьей матери в деревне Кинерма [Электронный ресурс] // CARELICA: научный электронный журнал. Петрозаводск: ПетрГУ, 2013. №1 (10). С.155–162.; URL: http://carelica.petrsu.ru/2013/Kosenkov_A.pdf. (дата обращения: 16.10.2014).
2. Марков Б. Г., Марков О. Б., Борисов А. Ю. Особенности геометрического моделирования утраченных памятников архитектуры // Ученые записки Петрозаводского государственного университета. Сер. «Естественные и технические науки.» 2013. № 8 (137). С. 88–92.
3. Марков Б. Г., Марков О. Б., Воронов Р. В. Модель одномерного нечеткого проективного пространства // Современные проблемы науки и образования. 2013. № 6; URL: http://www.science-education.ru/113-11542 (дата обращения: 16.10.2014).
4. Марков Б.Г., Марков О.Б. Точка в модели двумерного нечеткого проективного пространства // Современные научные исследования и инновации. 2015. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/06/56091 (дата обращения: 22.10.2015).
5. Марков Б. Г. Марков О. Б. Геометрическая интерпретация нечеткой прямой. Петрозаводск: ПетрГУ. 2003. 14 с. Деп. в ВИНИТИ 16.07.03 №1401–В2003.
6. Марков Б. Г. Марков О. Б. Геометрическая интерпретация нечеткой точки. Петрозаводск: ПетрГУ. 2003. 14 с. Деп. в ВИНИТИ 16.07.03 №1402–В2003.
7. Марков Б.Г. Прямая в модели двумерной нечеткой проективной геометрии // Современные научные исследования и инновации. 2014. № 11 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/11/40694 (дата обращения: 09.12.2014).
8. Четверухин Н. Ф. Проективная геометрия. М.: Просвещение, 1969. 368 с.

Все статьи автора «Марков Олег Борисович»