При решении многих практически важных задач часто приходится иметь дело с исходными данными, точные значение которых определить сложно или практически невозможно. В таких случаях иногда применяют методы нечеткого математического моделирования [2]. В задачах геометрического моделирования также используют нечеткие множества [3], [5], [10]. Предлагаемая в данной статье модификация проективной геометрии учитывает представление информации, с одной стороны как случайных величин, подчиненных нормальному закону распределения ошибок, с другой стороны как нечетких множеств.
При геометрическом моделировании часто исходная информация, имеет вид случайных величин, подчиненных нормальному закону распределения ошибок [6]. Фиксация и обработка такой информации, рассматривается в теории вероятностей и теории нечетких множеств. Классическая проективная геометрия не учитывает ошибки, отклонения от перпендикулярности, параллельности или прямолинейности. Она использует идеальные точки и прямые. Для учета особенностей исходной информации была проведена модификация проективной геометрии, учитывающая свойства нечеткой геометрической информации.
Особенностью проективного пространства является [9] то, что для него справедливы следующие утверждения:
а) каждая прямая проективного пространства содержит одну бесконечно удаленную точку.
б) каждая плоскость содержит одну бесконечно удаленную прямую.
в) проективное пространство в целом содержит одну бесконечно удаленную плоскость.
Для краткости бесконечно удаленные элементы будем, дальше, называть несобственными.
Основные объекты и основные отношения нечеткой проективной геометрии выражаются терминами “нечеткая точка”, “нечеткая прямая”, “нечеткая плоскость”, “принадлежность”. Точка представляется эллиптической областью, центр которой является ее номинальным положением, а границей – заданная ошибка [7]. Прямая – это область, ограниченная ветвями гиперболы, где она может, находится с заданной вероятностью. Номинальное положение прямой – мнимая ось гиперболы. Мнимая ось гиперболы проходит через центры эллиптических областей представляющих точки. Любой геометрический элемент представлен нечеткой областью. Пересечение нечетких элементов есть нечеткий элемент. Например, точкой пересечения пары прямых является точка-область, где эта точка пересечения может, появиться с заданной вероятностью. Результаты построения точки схода (точки – области) обрабатываются методами математической статистики.
Основными объектами двухмерной нечеткой проективной геометрии являются: нечеткая точка, нечеткая прямая, основное отношение – принадлежность. Проективная прямая содержит одну несобственную нечеткую точку. Проективная плоскость содержит одну несобственную нечеткую прямую. Две нечеткие прямые на плоскости пересекаются в одной нечеткой точке.
Пусть ![]() - двухмерная нечеткая собственная точка,
- двухмерная нечеткая собственная точка,
![]() - двухмерная нечеткая несобственная точка
- двухмерная нечеткая несобственная точка
Двухмерная нечеткая точка называется собственной, если находится на конечном расстоянии от начала координат и несобственной, если находится в бесконечности. Собственная точка ![]() задается пятью параметрами:
задается пятью параметрами: ![]() – математическое ожидание,
– математическое ожидание, ![]() ,
,![]() главные средние квадратичные отклонения,
главные средние квадратичные отклонения, ![]() - угол наклона эллипса рассеивания к оси 0X. Несобственная двухмерная нечеткая точка
- угол наклона эллипса рассеивания к оси 0X. Несобственная двухмерная нечеткая точка ![]() задается двумя параметрами:
задается двумя параметрами: ![]() - угол наклона прямой на которой лежит данная несобственная точка,
- угол наклона прямой на которой лежит данная несобственная точка, ![]() - среднее квадратичное отклонение тангенса угла направления прямой.
- среднее квадратичное отклонение тангенса угла направления прямой.
Нечеткая несобственная точка на плоскости является двухмерной величиной и поэтому подчиняется всем закономерностям одномерной нечеткой геометрии. На чертеже она изображается тремя отрезками прямой линии, проходящими через одну точку.
Для собственной двухмерной нечеткая точки ![]() принято, что закон распределения координат точки есть нормальный закон распределения, который характеризуется плотностью вероятности вида:
принято, что закон распределения координат точки есть нормальный закон распределения, который характеризуется плотностью вероятности вида:
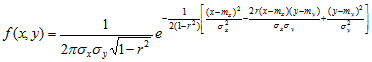 (1)
(1)
где m (mx, my) – математическое ожидание или центр рассеивания,
![]() - средние квадратичные отклонения,
- средние квадратичные отклонения,
r – коэффициент корреляции величин X и Y.
Данная гипотеза является общепринятой [1] в экспериментальных исследованиях.
Собственная двухмерная нечеткая точка изображается на чертеже в виде эллипса рассеивания (рис.1), который задается пятью параметрами: центр эллипса - mx, my, угол наклона большой оси эллипса к оси абсцисс (0X) - ![]() , большой и малой полуоси эллипса –
, большой и малой полуоси эллипса –![]() . Этот эллипс представляет собой область, где данная точка может находиться с заданной вероятностью.
. Этот эллипс представляет собой область, где данная точка может находиться с заданной вероятностью.
Частными случаями двумерной собственной нечеткой точки являются: собственная одномерная нечеткая точка [7] (![]() =0 , или
=0 , или ![]() =0), идеальная собственная двумерная точка (
=0), идеальная собственная двумерная точка (![]() =0 , и
=0 , и ![]() =0)
=0)
Совместим оси координат ![]() с главными осями эллипса рассеивания, тогда нормальный закон распределения будет характеризоваться плотностью вероятности вида:
с главными осями эллипса рассеивания, тогда нормальный закон распределения будет характеризоваться плотностью вероятности вида:
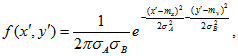 (2)
(2)
где m (mx, my)–математическое ожидание или центр рассеивания,
![]() - средние квадратичные отклонения,
- средние квадратичные отклонения,
![]() –угол наклона большой оси эллипса к оси 0X
–угол наклона большой оси эллипса к оси 0X
Величину угла наклона![]() , можно вычислить из выражения:
, можно вычислить из выражения:
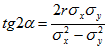 . (3)
. (3)
Поверхность распределения изображающая эту функцию имеет вид холма [1], если ее рассечь плоскостями параллельными плоскости X0Y, получаются эллипсы. Уравнение проекций этих эллипсов на плоскость X0Y имеет вид
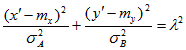 . (4)
. (4)
При ![]() мы получим эллипс с осями
мы получим эллипс с осями ![]() (сигма эллипс рассеивания) изображение точки
(сигма эллипс рассеивания) изображение точки ![]() .
.
На любую прямую - ![]() плоскости двухмерная нечеткая точка проецируется в одномерную нечеткую точку (рис. 1) со средним квадратичным отклонением
плоскости двухмерная нечеткая точка проецируется в одномерную нечеткую точку (рис. 1) со средним квадратичным отклонением
![]() , (5)
, (5)
где ![]() - среднее квадратичное отклонение одномерной точки прямой
- среднее квадратичное отклонение одномерной точки прямой ![]() ,
,
![]() - главные средние квадратичные отклонения двумерной точки плоскости,
- главные средние квадратичные отклонения двумерной точки плоскости,
![]() - угол между большой осью эллипса и прямой
- угол между большой осью эллипса и прямой ![]() .
.
На основные оси координат двумерная нечеткая точка проецируется в одномерные нечеткие точки с математическими ожиданиями ![]() и средними квадратичными отклонениями равными
и средними квадратичными отклонениями равными
![]() , (6)
, (6)
![]() , (7)
, (7)
где ![]() - угол наклона большой оси эллипса оси 0X.
- угол наклона большой оси эллипса оси 0X.
Две одномерные нечеткие точки, не принадлежащие одной прямой, имеющие общее математические ожидание (рис. 2), образуют одну двумерную нечеткую точку. Одномерные точки являться соответствующими проекциями двумерной точки.
Параметры двумерной нечеткой точки можно найти средствами аналитической геометрии. Две прямые ![]() (рис. 3) наклонены к оси 0X под углами
(рис. 3) наклонены к оси 0X под углами ![]() . Прямые пересекаются в точке m (X,Y). На прямых имеются две одномерные нечеткие точки
. Прямые пересекаются в точке m (X,Y). На прямых имеются две одномерные нечеткие точки ![]() , математические ожидания точек совпадают с точкой m, средние квадратичные отклонения точек
, математические ожидания точек совпадают с точкой m, средние квадратичные отклонения точек ![]() . Одномерные точки образуют двумерную нечеткую точку
. Одномерные точки образуют двумерную нечеткую точку ![]() .
.
Главные средние квадратичные отклонения равны ![]() .
.
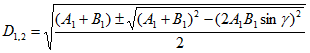 , (8)
, (8)
где А1, В2 - сопряженные радиусы эллипса.
![]() ,
, ![]() , (9)
, (9)
где ![]() - угол между прямыми
- угол между прямыми ![]()
![]() . (10)
. (10)
Угол наклона большой оси эллипса к большему сопряженному радиусу равен
![]() , где
, где ![]() равно
равно
.gif) . (11)
. (11)
Угол наклона большой оси эллипса к оси 0X равна,
если ![]() , то
, то![]() ,
,
иначе ![]() .
.
Чтобы применить общий подход теории нечетких множеств рассмотрим в качестве универсального множества
![]() . (12)
. (12)
В качестве функции принадлежности, учитывая нормальный закон распределения рассматриваемых в работе величин, целесообразно выбрать функцию
![]() ,
,
![]() , (13)
, (13)
для системы координат совмещенной с главными осями эллипса
![]() ,
, ![]() . (14)
. (14)
Нечеткой точкой с параметрами ![]() на плоскости называется подмножество
на плоскости называется подмножество ![]() такое, что
такое, что
![]() ,
, ![]() , (15)
, (15)
Подмножество ![]() также называется нечетким подмножеством соответствующим нечеткой точке с параметрами
также называется нечетким подмножеством соответствующим нечеткой точке с параметрами ![]()
Легко установить, что функция принадлежности изменяется в интервале [0,1] и ставит в соответствие каждому элементу ![]() число
число ![]() из интервала [0,1]. Точки перехода расположены на эллипсе с осями
из интервала [0,1]. Точки перехода расположены на эллипсе с осями ![]() и
и ![]() , максимальное значение функция принадлежности достигает при
, максимальное значение функция принадлежности достигает при ![]() и
и ![]() то есть
то есть
![]()
Рассмотрим принадлежность двух нечетких точек. Две точки, две прямые, точка и прямая в двухмерном пространстве в проективной геометрии находятся в некотором связи, которую принято выражать терминами инцидентность или принадлежность [9]. Инцидентность в классической проективной геометрии имеет два значения, 0 (нет) и 1 (да). Например, если расстояние между точками равно нулю, то инцидентность двух точек равна 1(да), во всех остальных случаях инцидентность равна 0(нет).
Взаимосвязь нечетких элементов в двухмерном пространстве, будем обозначать термином, принадлежность или совпадение в нечетком смысле. Однако в отличие от классического случая степень принадлежности может принимать любые значения в интервале [0;1].
Назовем мерой принадлежности двух собственных нечетких точек на плоскости величину.
![]() , (16)
, (16)
где ![]() функция принадлежности нечеткому множеству
функция принадлежности нечеткому множеству![]()
![]() функция принадлежности нечеткому множеству
функция принадлежности нечеткому множеству![]()
Две нечеткие точки на плоскости назовем
принадлежными, если ![]() и
и
непринадлежными, если ![]()
Даны две нечеткие двумерные собственные точки ![]() и
и ![]() (рис. 4). С точкой
(рис. 4). С точкой ![]() связана система координат
связана система координат ![]() , с точкой
, с точкой ![]() связана система
связана система ![]() .
.
С помощью формул преобразования координат подсчитаем координаты математического ожидания m1 в системе координат ![]() (рис. 5)
(рис. 5)
![]() . (17)
. (17)
Определим координаты математического ожидания m2 в системе координат ![]() (рис. 6)
(рис. 6)
![]() . (18)
. (18)
Подсчитаем меру принадлежности по формуле (14) с учетом (17) и (18)
![]() , (19)
, (19)
![]() . (20)
. (20)
Учитывая, что ![]() где
где ![]() - расстояние между математическими ожиданиями нечетких точек. Подставим (19),(20) в (16) с учетом
- расстояние между математическими ожиданиями нечетких точек. Подставим (19),(20) в (16) с учетом ![]() и получим формулу для подсчета принадлежности двух точек
и получим формулу для подсчета принадлежности двух точек
![]() . (21)
. (21)
Для определения принадлежности двух нечетких несобственных точек ![]() , учитывая их одномерность, равно
, учитывая их одномерность, равно
![]() , (22)
, (22)
где ![]() - тангенс угла между математическими ожиданиями несобственных точек
- тангенс угла между математическими ожиданиями несобственных точек ![]() .
.
Аналогично можно рассмотреть и нечеткую прямую и ее пересечение. Нечеткая прямая и определение распределения ее параметров будут рассмотрены в следующей статье.
Сформулированные предложения по теории нечеткой проективной геометрии, дали возможность разработать ряд алгоритмов для решения задач геометрического моделирования утраченных памятников архитектуры по их перспективным изображениям. Был создан комплекс программ, реализующих операции построений в нечеткой проективной геометрии и статистическую обработку результатов построения. Разработан комплекс программ, предназначенный для решения практических задач геометрического моделирования утраченных памятников архитектуры.
Применение нечеткой проективной геометрии и статистической обработки результатов опытов при учете неравноточности измерений, позволило увеличить достоверность результатов восстановления [4].
*Работа выполняется при финансовой поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности.
СПИСОК ИЛЛЮСТРАЦИЙ:
Рис. 1 Собственная двухмерная нечеткая точка.
Рис. 2 Две одномерные нечеткие точки с общим математическим ожиданием.
Рис. 3 Определение параметров двухмерной нечеткой точки по ее проекциям.
Рис. 4 Определение меры принадлежности пары двухмерных нечетких точек.
Рис. 5 Координаты математического ожидания m1и m2в системах координат ![]() и
и ![]() .
.
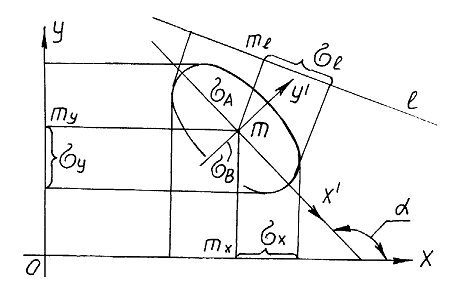
Рис. 1 Собственная двухмерная нечеткая точка.
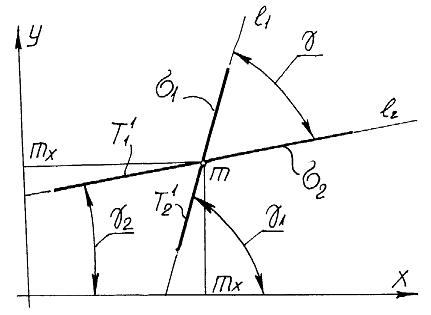
Рис. 2 Две одномерные нечеткие точки с общим математическим ожиданием.
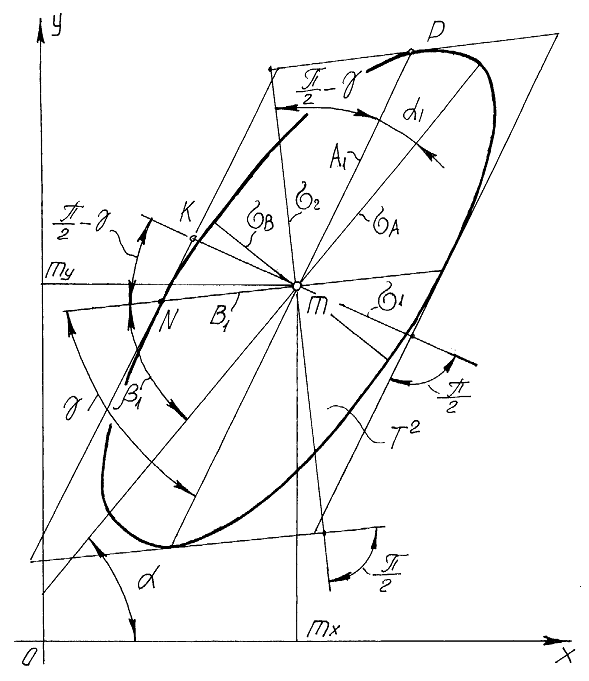
Рис. 3 Определение параметров двухмерной нечеткой точки по ее проекциям.
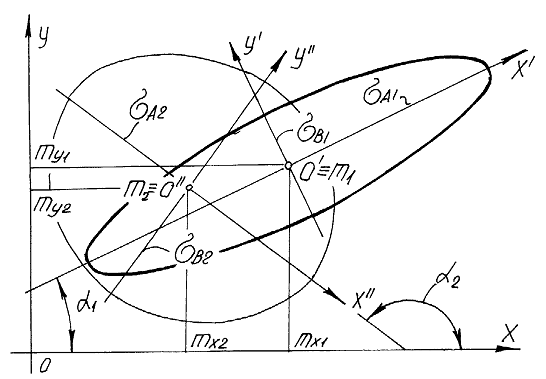
Рис. 4 Определение меры принадлежности пары двухмерных нечетких точек.
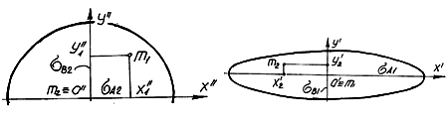
Рис. 5 Координаты математического ожидания m1и m2в системах координат ![]() и
и ![]() .
.
Библиографический список
- Вентцель Е. С. Теория вероятностей. М.; Наука, Физматгиз,1969 576 с.
- Воронова А. М., Воронов Р. В. Обоснование использования нечетких структур для моделирования размещения погрузочных пунктов и сети волоков на лесосеке // Актуальные вопросы современной науки. 2009. № 7–1. С. 86–93.
- Каркищенко А. Н., Бутенков С. А., Кривша В. В. Нечеткое представление и обработка геометрической информации // Искусственный интеллект: научно-теоретический журнал национальной академии наук Украины, 2000. № 3. С. 466–474.
- Косенков А. Ю., Марков Б. Г., Марков О. Б. Графическая реконструкция часовни Иконы Смоленской божьей матери в деревне Кинерма [Электронный ресурс] // CARELICA: научный электронный журнал. Петрозаводск: ПетрГУ, 2013. №1 (10). С.155–162.; URL: http://carelica.petrsu.ru/2013/Kosenkov_A.pdf. (дата обращения: 16.10.2014).
- Лукина О. В. Теоретико-конструктивные основы моделирования нечетких множеств в инженерной геометрии и их применение. Автореф. дисс. канд. техн. наук. Омск, 2006. 19 с.
- Марков Б. Г., Марков О. Б., Борисов А. Ю. Особенности геометрического моделирования утраченных памятников архитектуры // Ученые записки Петрозаводского государственного университета. Сер. «Естественные и технические науки.» 2013. № 8 (137). С. 88–92.
- Марков Б. Г., Марков О. Б., Воронов Р. В. Модель одномерного нечеткого проективного пространства // Современные проблемы науки и образования. 2013. № 6; URL: http://www.science-education.ru/113-11542 (дата обращения: 16.10.2014).
- Марков Б. Г. Марков О. Б. Геометрическая интерпретация нечеткой точки. Петрозаводск: ПетрГУ. 2003. 14 с. Деп. в ВИНИТИ 16.07.03 №1402–В2003.
- Четверухин Н. Ф. Проективная геометрия. М.: Просвещение, 1969. 368 с.
- Юрков В. Ю. Лукина О. В. Нечеткая геометрия как модель и средство развития визуального мышления, // Наука и образование. 2007. № 3. С. 3.
