Известно, что реактивная мощность трехфазной системы сложная величина, которая зависит от характера нагрузки, симметрии, наличия или отсутствия нулевого провода, уровня искажений в токе и питающем напряжении. Понятие реактивной мощности однозначно определено для симметричных систем в синусоидальном режиме. Однако такой режим, практически не встречается.
Для построения эффективных систем управления потоками мощности требуется точно определить причины возникновения неактивных токов для выбора средств компенсации. В качестве основы для анализа токов реальных систем можно использовать теорию мгновенных мощностей [1,2,3].
Основы были заложены Фризе в 1936 г.[4]. Было предложено рассматривать ток в цепи как сумму активного и неактивного токов в функции от времени, но на момент разработки теория Фризе не нашла применения и в течение 60 лет оставалась неизвестной, пока в конце прошлого столетия ее не начали использовать для управления активными фильтрами.
|
|
(1) |
| где: |
|
Активная составляющая тока , согласно теории, пропорциональна активной мощности и в фазе с напряжением, что значит, что неактивная составляющая тока полезной работы не выполняет и является причиной дополнительных потерь в линии.
Для трехфазной цепи можно представить напряжение и ток трехкомпонентными векторами, координаты которых пропорциональны токам и напряжениям в фазах, а скалярное произведение равно сумме мгновенных мощностей трех фаз:
|
(2) |
|
| где: |
|
|
(3) |
|
| где: |
|
|
(4) |
|
| где: p – мгновенная мощность системы. | |
Как и в теории Фризе ток системы делится на две составляющие: векторы активного и неактивного тока. Активная составляющая является проекцией вектора тока на вектор напряжения, неактивная составляющая находится к вектору напряжения под прямым углом, образуя с активной составляющей и вектором тока прямоугольный треугольник:
|
(5) |
|
| где: |
|
Неактивная составляющая в любой момент времени определяется помощью вектора мгновенной реактивной мощности (МРМ), который в свою очередь определяется как векторное произведение векторов тока и напряжения системы:
|
(6) |
|
| где: q – вектор МРМ системы. | |
Рассмотрим два случая активной трехфазной несимметричной нагрузки с нулевым проводом и без него.
Рисунок 1 – Годографы векторов напряжения и тока трехфазной системы с нулевым проводом и координаты вектора мгновенной реактивной мощности при активной несимметричной нагрузке
Рисунок 1 отражает изменение координат векторов напряжения и тока системы во времени, представлены годографы векторов за три четверти периода, чтобы лучше показать положение векторов в пространстве друг относительно друга. Изменение вектора мгновенной реактивной мощности можно проследить по изменению его координат во времени (на рисунке справа). Видно, что координаты изменяются по синусоидальному закону, и каждая имеет постоянную составляющую, отличную от нуля. Уравнение координаты вектора МРМ по оси а:
|
(7) |
|
где: – постоянная составляющая координаты вектора мгновенной реактивной мощности по оси а,
– амплитуда переменной составляющей координаты вектора по оси а,
![]() – круговая частота вектора напряжения,
– круговая частота вектора напряжения, ![]() – начальная фаза переменной составляющей координаты вектора.
– начальная фаза переменной составляющей координаты вектора.
В векторе МРМ можно выделить постоянную несимметричную составляющую:
|
|
(8) |
где: – постоянная несимметричная составляющая вектора мгновенной реактивной мощности,
– постоянная составляющая координаты вектора по оси b,
– постоянная составляющая координаты вектора по оси c.
В системе без нулевого провода вектор МРМ меняет свое поведение (рис.2).
Рисунок 2 – Годографы векторов мгновенных напряжений и токов трехфазной системы без нулевого провода и координаты вектора мгновенной реактивной мощности при активной несимметричной нагрузке
Вектор симметрично изменяется по синусоидальному закону и не имеет постоянной составляющей. В этом случае векторы тока и напряжения вращаются постоянно в одной плоскости.
Интересна для анализа система с чисто индуктивной нагрузкой (рис.3).
Рисунок 3 – Годографы векторов мгновенных напряжений и токов трехфазной системы с нулевым проводом и координаты вектора мгновенной реактивной мощности при индуктивной несимметричной нагрузке
Вектор тока за период описывает эллипс в плоскости отличной от плоскости вектора напряжения. При этом координаты вектора МРМ имеют постоянную и переменную составляющие. Постоянная составляющая в отличие от предыдущего случая значительно смещена в седьмой октант.
Рисунок 4 демонстрирует поведение вектора МРМ при отсутствии нулевого провода. Вектор имеет симметричную постоянную составляющую и переменную, изменяющуюся по синусоидальному закону.
Рисунок 4 – Годографы векторов мгновенных напряжений и токов трехфазной системы без нулевого провода и координаты вектора мгновенной реактивной мощности при индуктивной несимметричной нагрузке
Исходя из полученных результатов вектор МРМ, можно разделить, на три составляющие: симметричную постоянную ![]() , несимметричную постоянную
, несимметричную постоянную ![]() , появляющуюся в случае наличия нулевого провода и переменную составляющую
, появляющуюся в случае наличия нулевого провода и переменную составляющую ![]() .
.
|
(9) |
Сравнивая поведение вектора в симметричных[5] и несимметричных системах, можно сделать вывод о том, что симметричная постоянная составляющая вектора пропорциональна реактивной мощности системы. При наличии нулевого провода в несимметричной системе появляется постоянная несимметричная составляющая вектора МРМ.
Подводя итог вышесказанному, нужно отметить, что анализ вектора МРМ в несимметричных системах возможен. Вектор, а значит и неактивный ток трехфазной систем имеет составляющие: симметричные и несимметричные, постоянные и изменяющиеся во времени, появляющиеся в зависимости от нагрузки. Несимметричная постоянная составляющая вектора появляется только в несимметричных системах с нулевым проводом, в то время как симметричная постоянная составляющая появляется всегда при наличии реактивной нагрузки.
Библиографический список
- H. Akagi, Y. Kanazawa, A. Nabae, “Instantaneous reactive power compensator’s comprising switching device without energy storage components,” IEEE Trans. Ind. Applications,vol. .IA-20, May/June 1984, pp. 625-630.
- H. Akagi, H. Kim “” IEEE International Conference on Power Electronics and Drive Systems, PEDS’99, July 1999, Hong Kong.
- Жеменов Г.Г. Ильина О.В. «Теория мощности Фризе и современные теории мощности» Электротехника и электромеханика №6, 2007 с.63-65
- S. Frize, “Active and Apparent power in non-sinusoidal systems”. Przeglad Electrot (In Poland), no 7, 1931, p.p. 193-203.
- Шклярский А.Я., Барданов А.И. «Анализ вектора мгновенной Реактивной мощности трехфазной сети при различной симметричной нагрузке», Естественные и технические науки №3, М.:Спутник, 2015. с.127-131


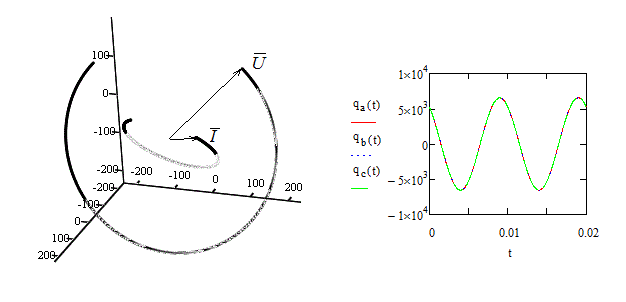

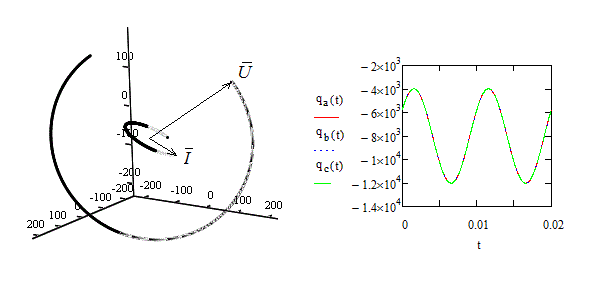
C интересом прочитал статью. Не понял поставленную задачу и практический результат. Сам занимаюсь мгновенной неактивной мощностью в целях управления САФ. Ищу единомышленников.
Бондаренко Александр. к.т.н., докторант кафедры электротехники и электрооборудования судов
СПб государственного морского технического университета.
aebon@mail.ru,
+7 812 921 300 37 31
Здравствуйте, Александр! Благодарю за проявленный к моей статье интерес. С замечанием согласен, статья не решает конкретных практических задач, только раскрывает некоторые стороны теории мгновенной неактивной мощности.