Известно, что основной принцип неживой природы – это принцип наименьшего действия. Системы неживой природы постоянно стремятся обрести наиболее устойчивое состояние. При этом каждое тело принимает такую форму, при которой затраты энергии будут минимальными. Это можно увидеть в рассматриваемой задаче на примере такого природного объекта как пчелиные соты.
Пчелиные соты состоят из ячеек в виде десятигранников. Представить себе такую ячейку можно следующим образом. Возьмём правильную шестиугольную призму (рис. 1). Через каждую из трёх диагоналей верхнего основания и точку S, взятую на оси этой призмы, проведём плоскость. Эти плоскости и будут ограничивать сверху ячейку. Таким образом, ячейка ограничена снизу правильным шестиугольником, с боков – шестью равными прямоугольными трапециями и сверху – тремя равными ромбами. Объём ячейки равен объёму исходной призмы. 

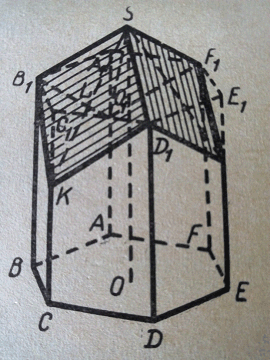
Рисунок 1 – Геометрическая форма пчелиной соты

Возникает вопрос: каким должен быть плоский угол при вершине S ячейки, чтобы расход воска на изготовление ячейки был наименьшим? Иными словами, каким должно быть положение точки S, чтобы площадь поверхности ячейки была наименьшей?
Для ответа на этот вопрос введём обозначения:  Пользуясь ими, найдём сначала площадь каждой трапеции. Она равна  или  (так как . Площадь же каждого ромба равна  или в принятых обозначениях . Площадь нижнего основания можно не принимать в расчёт, так как от положения точки S она не зависит. Поэтому интересующая нас площадь выразится формулой  или  Эта площадь будет иметь наименьшее значение, если наименьшим будет выражение . Обозначив эту разность через , получим: , или , откуда  Так как расстояние  должно быть действительным числом, то поэтому получаем неравенство , или . Значит, наименьшее значение , при котором и  будет иметь наименьшее значение, должно быть равно . Соответствующее ему значение  легко находится. Получаем, что при  расход воска будет наименьшим.
Зная , нетрудно найти плоский угол при вершине . Это можно сделать так: 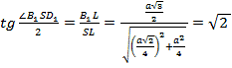. Поэтому . 
Проведём натурные измерения размеров пчелиной соты и проверим, насколько они соответствуют полученным расчётам. Фотографии пчелиных сот, с которых были взяты численные измерения, представлены на рис.2, рис.3. и рис.4. На рис.2 показана нижняя часть соты (правильный шестиугольник), на рис.3 – верхняя часть, на рис.4 – длина медовой соты. 

Рисунок 2 – Нижняя часть соты (правильный шестиугольник)

Рисунок 3 – Верхняя часть соты
Рисунок 4 – Длина медовой соты

По аналогии с рис. 1 были произведены измерения длин CD, BB₁, CK, B₁D₁, SK, SO₁. В результате были получены следующие значения:

В соответствии с полученными формулами . 
Если , то  должен быть равен:

 мм.

Сравним данное значение с измеренным:

.

Найдём плоский угол  при вершине  измеряемой медовой соты:

Отсюда .
Сравним данное значение угла с значением, полученным математическими доказательствами:

Таким образом, непосредственные измерения подтверждают данные, полученные математическим расчётом. Пчела оказалась хорошим «математиком», исходя из принципа наименьшей затраты воска. 
Для интереса можно вычислить площадь поверхности наблюдаемой соты. Она будет равна:

.

Ранее установлено, что экономия воска, которая получается при такой форме ячейки (по сравнению с шестиугольной призмой) составляет примерно 2%. Более точно эту экономию можно выразить так: из воска, сэкономленного при устройстве 54 ячеек, пчёлы могут дополнительно построить ещё одну ячейку. Экономия значительная.
Таким образом, природа существует по принципу минимума энергии. С помощью математических расчётов иногда можно получить численные значения различных величин природных тел.

1. Быкова Ю.С., Гафарова Д.З., Снежкина О.В. Прикладная математика в задачах геодезии // Современные научные исследования и инновации. 2014. № 12 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/12/42283
2. Нагибин Ф.Ф. Экстремумы. Учебное пособие. – Издательство «Просвещение» Москва, 1966 – 119.
3. Быкова Ю.С., Снежкина О.В. К вопросу о междисциплинарных связях математики и геодезии // Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/56834
4. Баранова, Т.И. Гармонизация методов расчета железобетонных балок с различным пролетом среза / Т.И. Баранова, О.В. Снежкина // Вестник Отделения строительных наук Российской академии архитектуры и строительных наук. – 1998.- № 2.- С. 41.

Все статьи автора «Снежкина Ольга Викторовна»