С развитием промышленности и машиностроения все более широко внедряются зубчатые передачи внутреннего зацепления, поскольку они являются более компактными и имеют большую нагрузочную способность, по сравнению с зубчатыми передачами внешнего зацепления. Основное применение зубчатые колеса внутреннего зацепления нашли в оборонной промышленности, судостроении, автотракторной промышленности и в промышленности по производству крупного бурового оборудования, дорожного оборудования и машин. От качества изготовления зубчатых колес в значительной мере зависят эксплуатационные свойства машин и их надежность [5].
Традиционно, для обработки зубчатых колес внутреннего зацепления применяются долбяки, реже дисковые фрезы и фрезы-улитки, а также пальцевый инструмент. Помимо данных методов, необходимо отметить метод зуботочения, который впервые был научно обоснован во ВНИИИНСТРУМЕНТ [1]. Метод основывается на использовании специального зуборезного инструмента – обкаточного резца, который по конструкции напоминает косозубый долбяк, с числом зубьев, равным числу заходов, в связи с чем производительность метода до 7 раз выше по сравнению с зубодолблением. А поскольку, при зуботочении контакт обрабатываемого колеса и инструмента не точечный, а линейный, то огранка профиля изделия отсутствует.
Применение современного оборудования с ЧПУ позволяет не только использовать метод зуботочения обкаточным резцом для обработки зубчатых колес внутреннего зацепления, но и упростить конструкцию инструмента за счет более сложной кинематики.
При профилировании режущего инструмента одним из этапов является определение уравнения поверхности, огибающей боковую поверхность зуба зубчатого колеса при его движении относительно обкаточного резца. Для нахождения этого уравнения удобно воспользоваться кинематическим методом, основанном на концепции, утверждающей что если контакт двух сопряженных поверхностей непрерывен, то в точках контакта нормальная составляющая скорости относительного движения поверхностей равна нулю [6]. Аналитически это условие записывается так:

. (1)

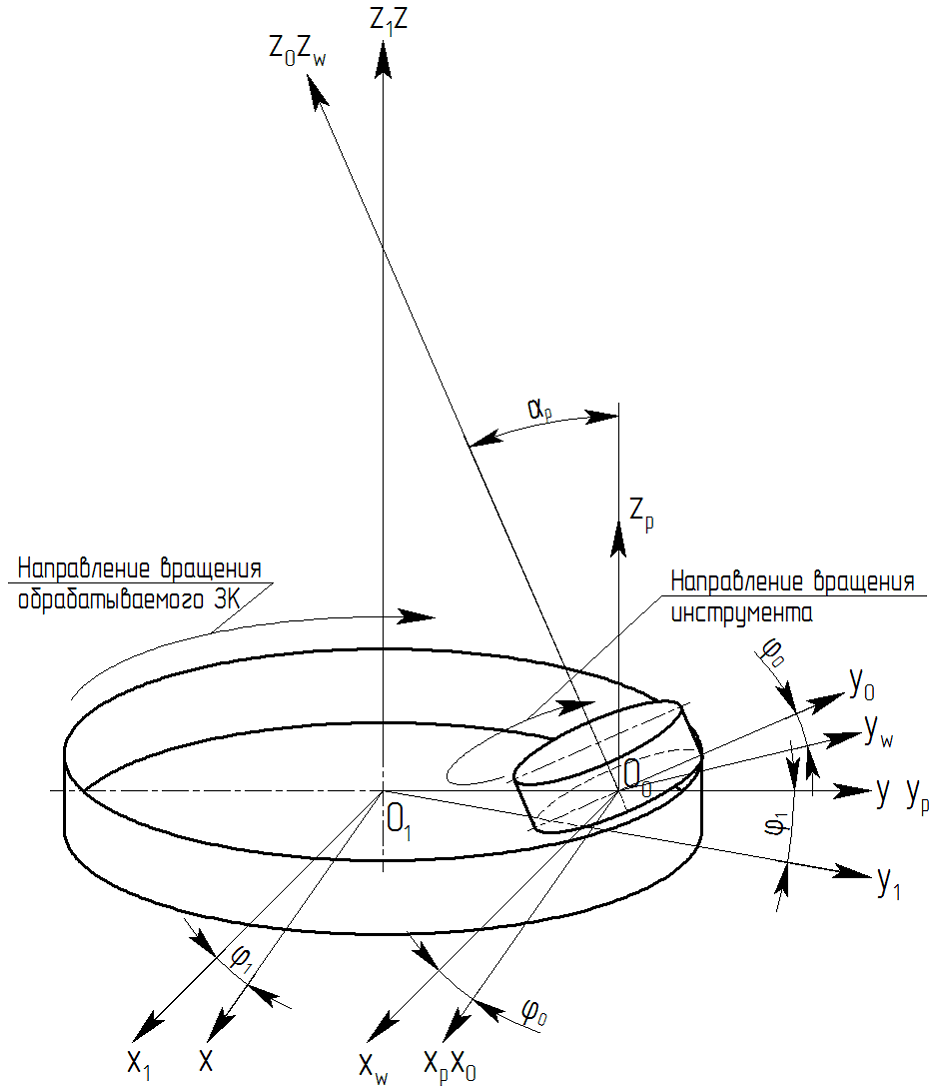
В данной работе рассматривается определение вектора относительной скорости . Для определения скорости относительного движения звеньев необходимо задаться схемой внутреннего станочного зацепления (рис. 1).

Рисунок 1 – Схема внутреннего станочного зацепления обкаточного резца с обрабатываемой деталью

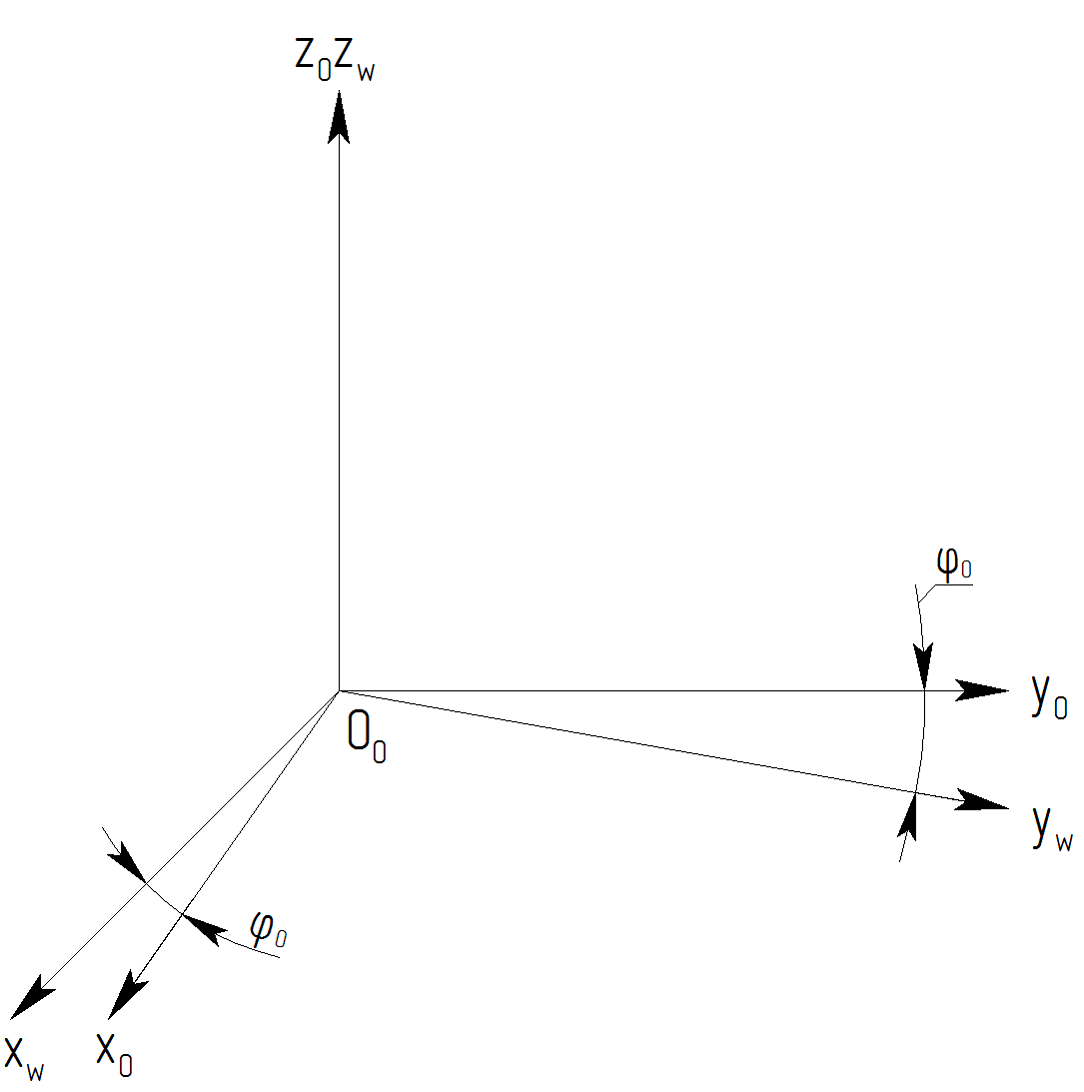
Здесь: O₁xyz – неподвижная система координат детали (ось Оz совпадает с осью обрабатываемой детали); O₁x₁y₁z₁ – подвижная система координат, жестко связанная с обрабатываемой деталью (повернута относительно системы координат O₁xyz на угол f₁); O₀x_py_pz_p – вспомогательная система координат (система позиционирования), в которой задается угол установки a_p; O₀x₀y₀z₀ – неподвижная система координат инструмента (ось Оz_p совпадает с осью обрабатываемой детали); O₀x_wy_wz_w – подвижная система координат, жестко связанная с обкаточным резцом (повернута относительно системы координат O₀x₀y₀z₀ на угол f₀). Угол поворота обрабатываемого зубчатого колеса f₁ и обкаточного резца f₀ связаны соотношением (2):

, (2)
, (3)

где u – передаточное число станочного зацепления; z₁, z₀ - число зубьев обрабатываемой детали и число зубьев (заходов) обкаточного резца соответственно.
Соотношения между указанными системами координат определяются следующими математическими зависимостями:
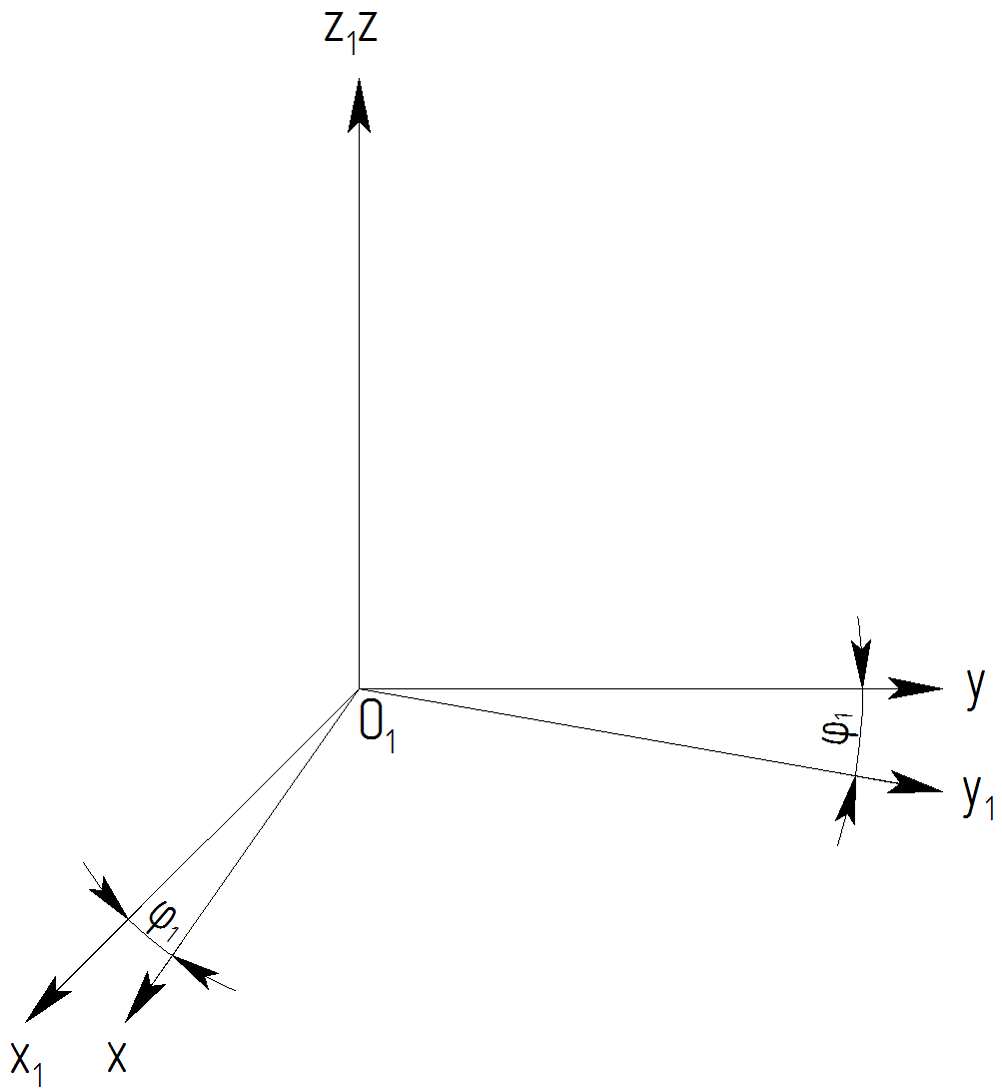
1. Преобразование координат между системами O₁x₁y₁z₁ и O₁xyz (рис. 2):

Рисунок 2 – Схема преобразования систем координат O₁x₁y₁z₁ и O₁xyz

Переход от системы O₁x₁y₁z₁ к системе O₁xyz и обратно характеризуется поворотом на угол f₁.
Для удобства преобразования координат запишем в матричном виде, используя квадратные матрицы четвертого порядка, поскольку такие матрицы учитывают, не только повороты, но и линейные перемещения. 
Чтобы воспользоваться матрицами четвертого порядка, необходимо предварительно вести однородные координаты. При однородных координатах положение точки в системе x_i, y_i, z_i задается четырьмя величинами: x’_i, y’_i, z’_i, t’_i. Четыре новые величины не равны одновременно нулю и связаны с x_i, y_i, z_iсоотношениями (4):

 ,  , . (4)

Следовательно, из четырех новых величин: x’_i, y’_i, z’_i, t’_i – независимыми являются только три.
Условимся, что t’_i = 1. Это позволит совершать переход от однородных координат к обычным и обратный переход. Тогда при однородных координатах положение любой точки в соответствующих системах координат можно записать в матричном виде, используя матрицу четвертого порядка.
Выразим координаты системы O₁xyz через координаты системы O₁x₁y₁z₁:

Матрица M₁ прямого преобразования:

Здесь и далее будем записывать только матрицы преобразования, не приводя уравнения зависимостей координат одной системы от другой.
Матрица M’₁ обратного преобразования:

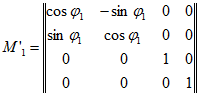
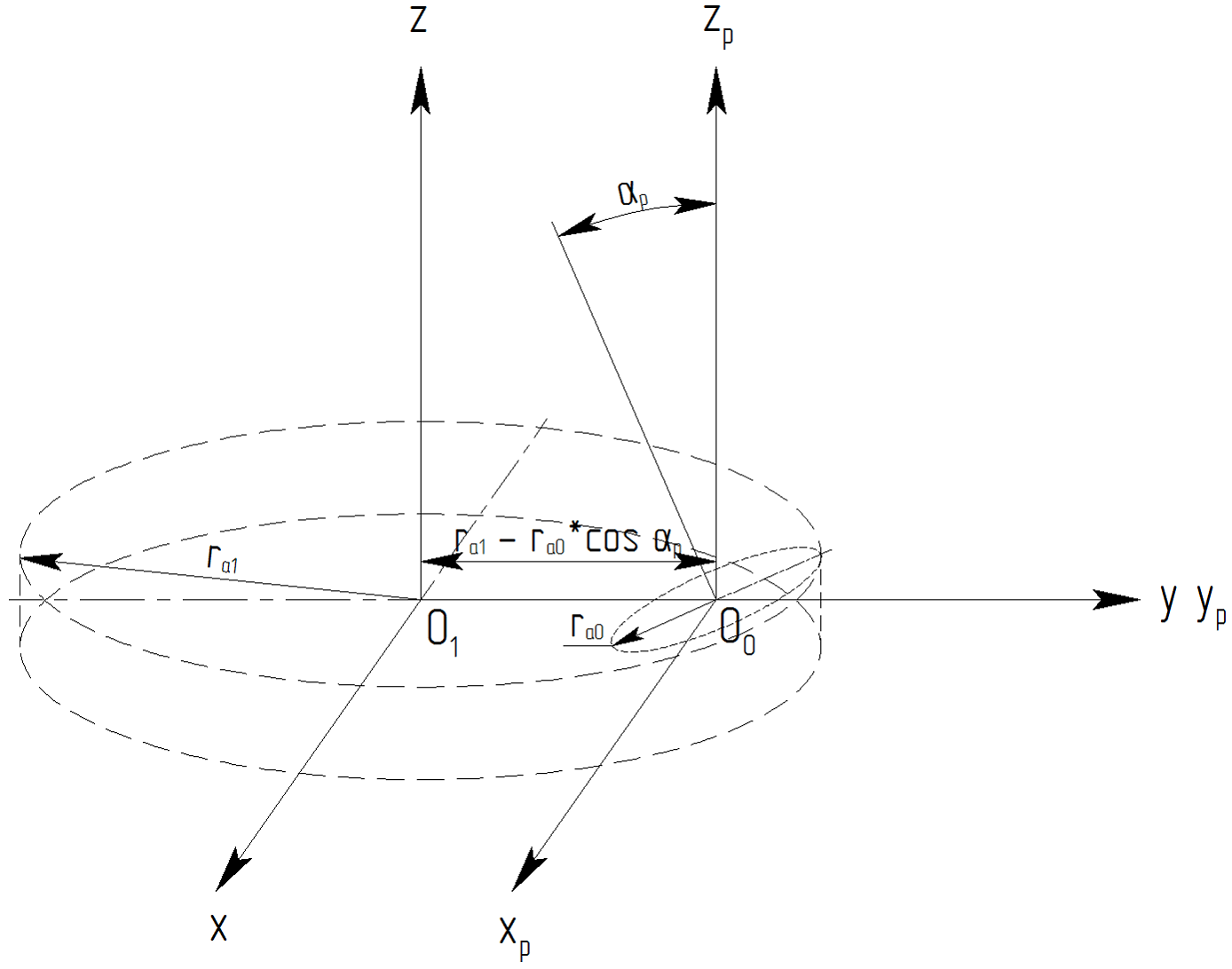
2. Преобразование координат между системами O₁xyz и O₀x_py_pz_p (рис. 3):

Рисунок 3 – Схема преобразования систем координат O₁xyz и O₀x_py_pz_p

Переход от системы O₁xyz к системе O₀x_py_pz_p характеризуется смещением центра на величину а, где:

. (5)

Матрица M₂ прямого преобразования:

Матрица M’₂ обратного преобразования:

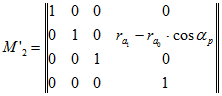
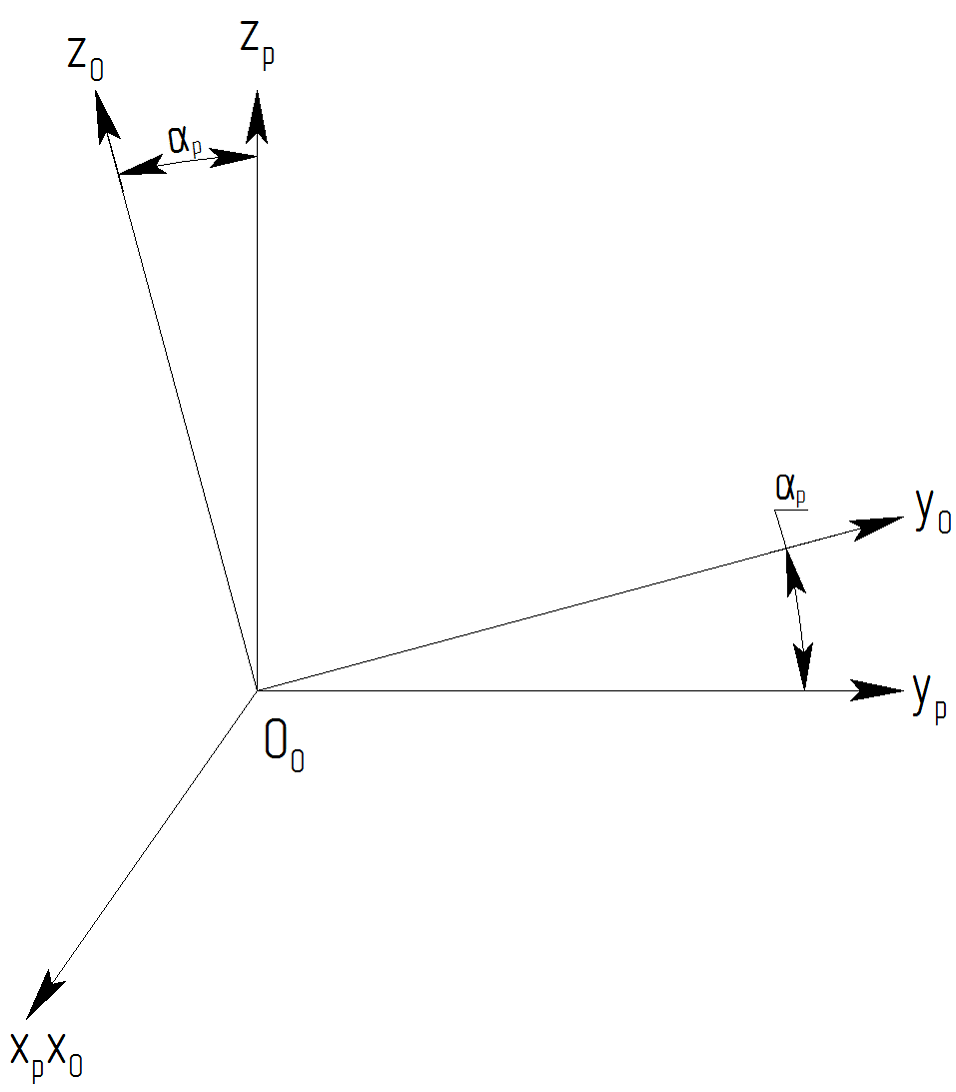
3. Преобразование координат между системами O₀x_py_pz_p и O₀x₀y₀z₀ (рис. 4):

Рисунок 4 – Схема для преобразования систем координат O₀x_py_pz_p и O₀x₀y₀z₀

Переход от системы O₀x_py_pz_p к системе O₀x₀y₀z₀ характеризуется поворотом на угол установки a_p.
Матрица M₃ прямого преобразования:

Матрица M’₃ обратного преобразования:

4. Преобразование координат между системами O₀x₀y₀z₀ и O₀x_wy_wz_w (рис. 5):

 
Рисунок 5 – Схема для преобразования систем координат O₀x₀y₀z₀ и O₀x_wy_wz_w

Переход от системы O₀x₀y₀z₀ к системе O₀x_wy_wz_w и обратно характеризуется поворотом на угол f₀.
Матрица M₄ прямого преобразования:

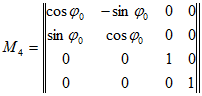
Матрица M’₄ обратного преобразования:

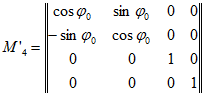
Задавшись схемой станочного зацепления обрабатываемого зубчатого колеса и обкаточного резца и составив матрицы преобразования координат, определяем скорость относительного движения звеньев.
Звено 1 (обрабатываемое зубчатое колесо) принадлежит неподвижной системе координат О₁xyz и вращается вокруг оси z c угловой скоростью (рис. 6). Звено0 (обкаточный резец) принадлежит неподвижной системе O₀x₀y₀z₀ и вращается вокруг оси z₀ с угловой скоростью .

Рисунок 6 – Схема определения вектора относительной скорости

Скорость точки звена 1 в системе О₁xyz определяется уравнением:

 , (6)

где:  – радиус-вектор точки звена 1.
В общем виде, для определения скорости точки звена 0 в системе О₁xyz необходимо привести вектор  к центру О₁, заменив его вектором  и вектором моментом:

, (7)

где  – радиус-вектор, являющийся кратчайшим расстоянием между системами координат О₁xyz и O₀x₀y₀z₀. Тогда, скорость точки звена 0 определяется уравнением:

(8)

Поскольку оси z и z₀, указанных выше систем пересекаются, то кратчайшее расстоянии между этими осями равняется нулю (). Следовательно, скорость точки звена 0 определяется уравнением:

, (9)

Скорость движения точки, жестко связанной со звеном 1, относительно той же точки, жестко связанной со звеном 0, определится уравнением:

(10)

Относительное движение звена 1 по отношению к звену 0 определяется вектором , проходящим через точку приведения O₁.
Найдем проекции , приняв во внимание, что:

, (11)
, (12)

где i, j, k – орты координатных осей.
Тогда:

(13)

Не нарушая общности решения задачи, примем ω₁ = 1 рад/сек, тогда:

(14)

Аналогично определяем скорость движения точки, жестко связанной со звеном 0, относительно той же точки, жестко связанной со звеном 1.

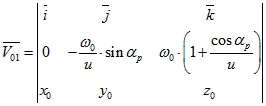(15)

Не нарушая общности решения задачи, примем ω₀ = 1 рад/сек, тогда:

(16)

Полученные расчетные зависимости для определения вектора относительной скорости необходимы для решения задачи профилирования обкаточного резца, обоснования величин его конструктивных и геометрических параметров, а также формализации условий отсутствия подрезания профиля изделия.

1. Цвис Ю.В. Профилирование режущего обкатного инструмента. М.: МАШГИЗ, 1961. – 156с.
2. Волков Н.Н. Исследование и разработка инструмента для нарезания цилиндрических зубчатых колес с внутренними зубьями по методу зуботочения.: Дис. канд. тех. наук. – М., 1981. – 222с.
3. Кирютин А.С. Математическая модель профилирования обкаточных резцов // Современные научные исследования и инновации. 2014. № 10 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/10/38627
4. Литвин Ф.Л. Теория зубчатых зацеплений. М.: «НАУКА», 1968. – 584с.: ил.
5. Производство зубчатых колес: Справочник / С.Н. Калашников, А.С. Калашников, Г.И. Коган и др.; Под общ. Ред. Б.А. Тайца. – 3-е изд., перераб. И допол. – М.: Машиностроение, 1990. – 464с.: ил.
6. Радзевич С.П. Кратко о кинематическом методе и об истории уравнения контакта в форме n · V = 0 // Теория механизмов и машин. 2010. №1. Том 8 [Электронный ресурс]. URL:http://tmm.spbstu.ru/15/radzevich_15.pdf
7. Петухов, Ю.Е. Формообразование численными методами / Ю.Е. Петухов. – М. : «Янус-К», 2004. – 200 с.
8. Гречишников, В.А. Математическое моделирование в инструментальном производстве / Гречишников В.А., Колесов Н.В., Петухов Ю.Е.. – М. : МГТУ «СТАНКИН». УМО АМ, 2003. – 116 с.
9. Петухов, Ю.Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства : дис. … докт. техн. наук : 05.03.01 / Петухов Ю.Е.. – М., 2004. – 393 с.
10. Петухов, Ю.Е. Численные модели режущего инструмента для обработки сложных поверхностей / Петухов Ю.Е., Колесов Н.В. // Вестник машиностроения. – 2003. – №5. – С. 61-63.
11. Петухов, Ю.Е. Профилирование режущих инструментов среде Т-flex CAD-3D / Петухов Ю.Е. // Вестник машиностроения. – 2003. – №8. – С. 67-70.
12. Петухов, Ю.Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Петухов Ю.Е., Домнин П.В. // Вестник МГТУ «СТАНКИН». – 2011. – №3. – С. 102-106.
13. Колесов, Н.В. Система контроля сложных кромок режущих инструментов / Колесов Н.В., Петухов Ю.Е. // ИТО: Инструмент. Технология. Оборудование. – 2003. – №2. – С. 42-45.
14. Петухов, Ю.Е. Компьютерная модель формообразования сложной поверхности / Петухов Ю.Е., Домнин П.В. // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т. : сб. науч. ст. – Тула, 2010. – Т. 1. – С. 197-200.
15. Колесов, Н.В. Компьютерная модель дисковых фасонных затылованных фрез / Колесов Н.В., Петухов Ю.Е., Баринов А.В. // Вестник машиностроения. – 1999. – №6. – С. 57-61.
16. Домнин, П.В. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений /Петухов Ю.Е., Домнин П.В. // Справочник. Инженерный журнал с приложением. – 2011. – №11. – С. 26-29.
17. Колесов, Н.В. Математическая модель червячной фрезы с протуберанцем / Колесов Н.В., Петухов Ю.Е. // СТИН. – 1995. – №6. – С. 26-29.
18. Колесов, Н.В. Два типа компьютерных моделей режущего инструмента Колесов/ Н.В., Петухов Ю.Е. // СТИН. – 2007. – №8. – С. 23-26.
19. Петухов, Ю.Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю.Е. Петухов, П.В. Домнин // СТИН. – 2011 – №7. – С. 14-17.
20. Петухов, Ю.Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2012. – №3. – С. 28-32.
21. Петухов, Ю.Е. Некоторые направления развития САПР режущего инструмента / Ю.Е. Петухов // СТИН. – 2003. – №8. – С. 26-30.
22. Петухов, Ю.Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2014. – №1 (28). – С. 39-43.
23. Petukhov, Y.E. Shaping precision in machining a screw surface / Y.E. Petukhov, P.V. Domnin // Russian Engineering Research. – 2011. – T. 31. – №10. – С. 1013-1015.
24. Kolesov, N.V. Computer models of cutting tools / N.V. Kolesov, Y.E. Petukhov // Russian Engineering Research. – 2007. – T. 27. – №11. – С. 812-814.
25. Petukhov, Y.E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y.E. Petukhov, A.V. Movsesyan // Russian Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.
26. Петухов Ю.Е. Cпособ шлифования фасонных валов. Патент на изобретение RUS 863310  04.05.1979
27. Петухов Ю.Е. Задачи по формообразованию при обработке резанием /Петухов Ю.Е., Колесов Н.В., Юрасов С.Ю.// Вестник машиностроения. 2014. № 3. С. 65-71.
28. Петухов Ю.Е. Устройство для правки фасонных шлифовальных кругов. Патент на изобретение RUS 823101 21.03.1979
29. Петухов Ю.Е. Способ обработки цилиндрических поверхностей патент на изобретение RUS 904999 04.05.1979
30. Петухов Ю.Е. Компьютерное моделирование обработки винтовой канавки на заготовке концевой фрезы./ Петухов Ю.Е, Домнин П.В.// Известия Московского государственного технического университета МАМИ. 2011. № 2. С. 156-164.
31. Петухов Ю.Е. Прибор для профилирования червячных фрез. Патент на изобретение RUS 878467 07.12.1978
32. Petukhov Yu.E. Some directions of cutting tool cad system development./ Petukhov Yu.E.// Russian Engineering Research. 2003. Т. 23. № 8. С. 72-76.
33. Petukhov Yu.E. Curvilinear cutting edge of a helical bit with uniform life./ Petukhov Yu.E.// Russian Engineering Research. 2014. Т. 34. № 10. С. 645-648.
34. Kolesov N.V. The mathematical model of a hob with protuberances./Kolesov N.V., Petukhov Yu.E.// Russian Engineering Research. 1995. Т. 15. № 4. С. 71-75.
35. Петухов Ю.Е. Определение задних кинематических углов при обработке винтовых фасонных поверхностей стандартными фрезами прямого профиля./ Петухов Ю.Е., Домнин П.В.// Вестник МГТУ Станкин. 2014. № 2 (29). С. 27-33.

Все статьи автора «Кирютин Алексей Сергеевич»