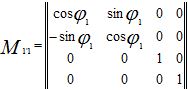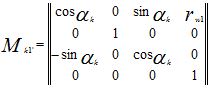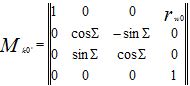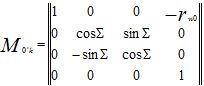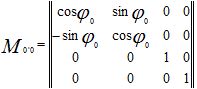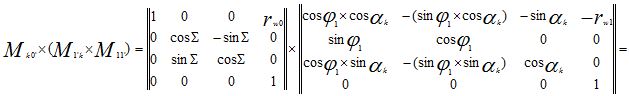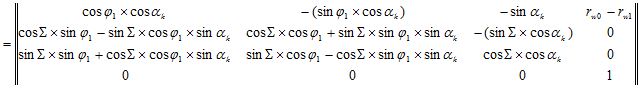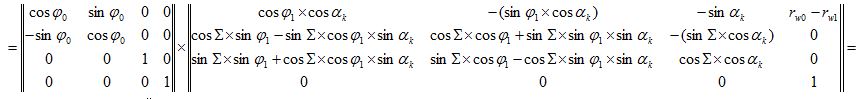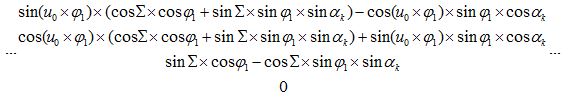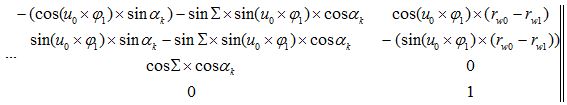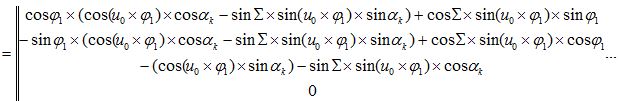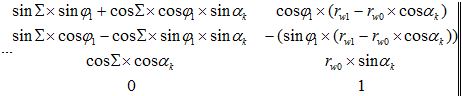Зубчатые передачи нашли широкое распространение в машинах и механизмах различных отраслей современного машиностроения. Традиционная технология обработки резанием цилиндрических зубчатых колес основана на применении двух основных методов, а именно, метода обкатки и метода единичного деления.
Помимо упомянутых традиционных методов изготовления цилиндрических зубчатых колес, необходимо отметить метод зуботочения, впервые научно обоснованный во ВНИИИНСТРУМЕНТ [21]. Сущность этого метода заключается в том, что для его реализации используется специальный инструмент (обкаточный резец) типа косозубого долбяка с числом зубьев, равным числу заходов при согласованных вращениях инструмента и изделия на их скрещивающихся в пространстве осях. Метод в силу различных причин не получил широкого распространения. Однако, учитывая все более широкое применение современного оборудования с ЧПУ, использование данного метода в современных условиях представляется весьма перспективным.
Особенно актуальным метод находит свое применение при нарезании зубчатых колес внутреннего зацепления, поскольку другие методы обработки, в сравнении с зуботочением, являются менее производительными. Так при зубодолблении, в силу наличии холостых ходов при обработке, производительность гораздо меньше, чем при обработке обкаточным резцом.
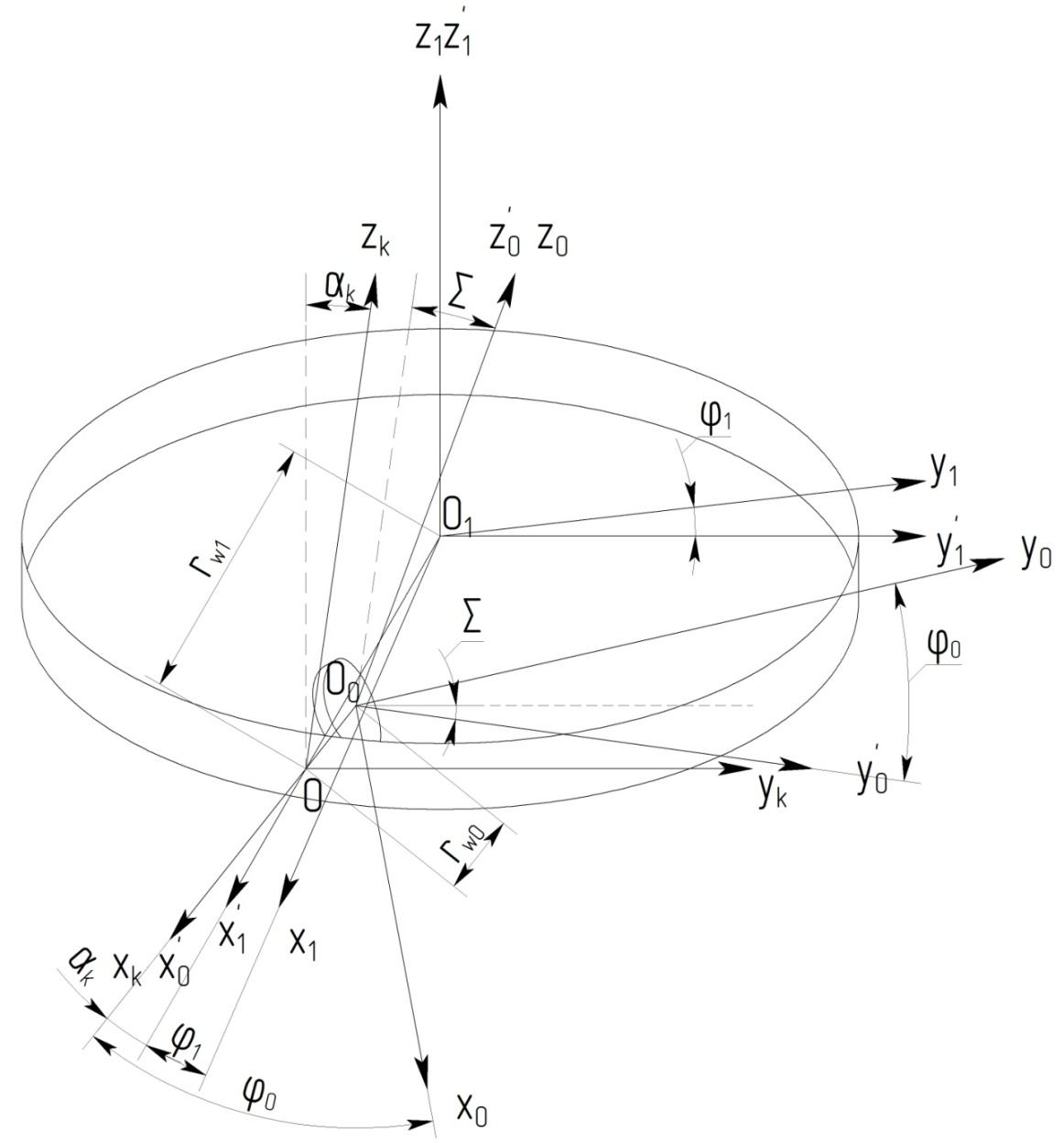
Применение метода зуботочения для нарезания колес с внутренними зубьями требует вывода математических зависимостей определения профиля зубьев обкаточных резцов. Станочное зацепление инструмента и детали похоже на винтовую зубчатую передачу на скрещивающихся осях. Для вывода зависимостей определения координат точек режущих кромок инструмента используются правые системы координат. При этом внутреннее станочное зацепление характеризуется кинематической схемой изображенной на рис. 1, рассмотренной в работе [22].
Рисунок 1 – Схема внутреннего станочного зацепления обкаточного резца с обрабатываемой деталью
Здесь: Оx’1y’1z’1 – неподвижная система координат детали (ось Оz’1 совпадает с осью обрабатываемой детали, ось Ox’1 – с межосевой линией); Ox1y1z1 – подвижная система координат, жестко связанная с обрабатываемой деталью (повернута относительно системы координат Оx’1y’1z’1 на угол φ1 – фазу зацепления); Оxkykzk – вспомогательная система с центром в полюсе зацепления, в которой задается кинематический задний угол αk; О0x’0y’0z’0 – неподвижная система координат инструмента; О0x0y0z0 – подвижная система координат, жестко связанная с обкаточным резцом (повернута относительно системы координат О0x’0y’0z’0 на угол φ0 – фазу зацепления); Σ – угол скрещивания осей обрабатываемой детали и обкаточного резца. Фаза зацепления φ1 и угол φ0 поворота инструмента связаны соотношением (1):
где ![]() передаточное число станочного зацепления; z1, z0 – число зубьев обрабатываемой детали и число зубьев (заходов) обкаточного резца соответственно.
передаточное число станочного зацепления; z1, z0 – число зубьев обрабатываемой детали и число зубьев (заходов) обкаточного резца соответственно.
Соотношения между указанными системами координат определяются следующими математическими зависимостями:
Преобразование 1: между системами Ox1y1z1 и Оx’1y’1z’1 (рис. 2):
Рисунок 2 – Схема преобрпахования систем координат Оx’1y’1z’1 и Ox1y1z1
Переход от системы Ox1y1z1 к системе Оx’1y’1z’1 и обратно характеризуется поворотом на угол φ1.
Для удобства запишем преобразования координат в матричном виде. При этом используем квадратные матрицы четвертого порядка, так как они учитывают, кроме поворотов, еще и линейные перемещения. Для того чтобы воспользоваться матрицами такого порядка, нужно предварительно вести так называемые однородные координаты. При однородных координатах положение точки в системе xi, yi, zi задается четырьмя величинами: x’i, y’i, z’i, t’i. Четыре новые величины не равны одновременно нулю и связаны с xi, yi, zi соотношениями (2):
Следовательно, из четырех новых величин: x’i, y’i, z’i, t’i – независимыми являются только три.
Аналогично, для определения положения точки в системе xj, yj, zj будем пользоваться однородными координатами: x’j, y’j, z’j, t’j, где:
Условимся, что t’j = t’i = 1. Это позволит совершать переход от однородных ординат к обычным и обратный переход. Тогда при однородных координатах положение любой точки в соответствующих системах координат можно записать в матричном виде, используя матрицу четвертого порядка.
Матрица M11‘ прямого преобразования:
Матрица M1′1 обратного преобразования:
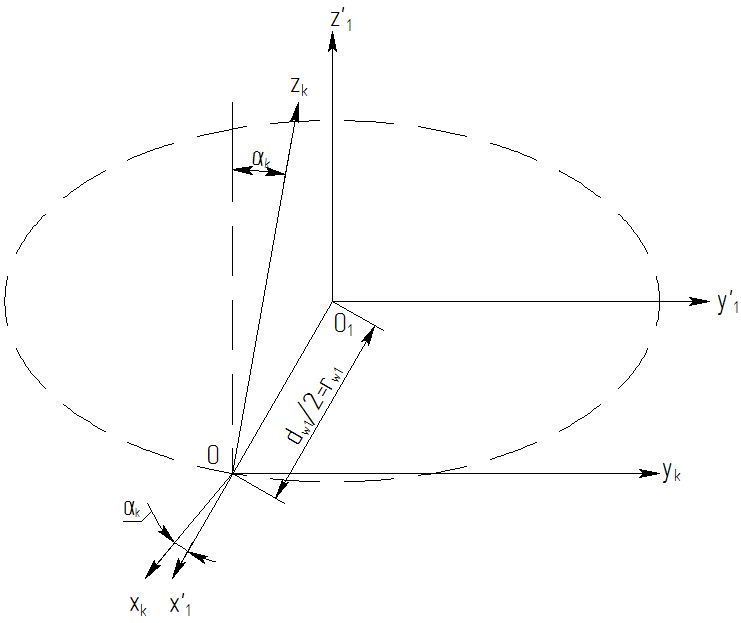
Преобразование 2: между системами Оx’1y’1z’1 и Оxkykzk (рис. 3):
Рисунок 3 – Схема преобразования систем координат Оx’1y’1z’1 и Оxkykzk
Переход от системы Оx’1y’1z’1 к системе Оxkykzk одновременно характеризуется смещением в полюс зацепления зубчатого колеса и обкаточного резца на радиус начальной окружности зубчатого колеса rw1 и поворотом на задний кинематический угол αk.
Матрица M1′k прямого преобразования:
Матрица Mk1′ обратного преобразования:
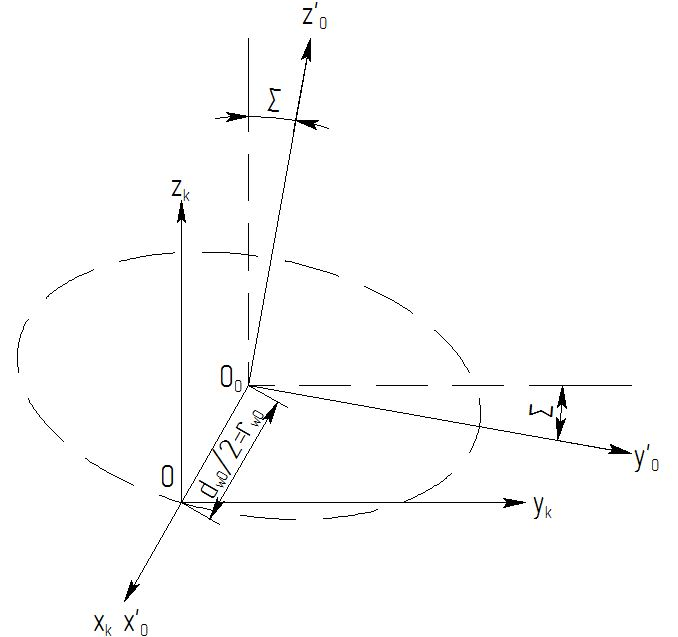
Преобразование 3: между системами Оxkykzk и О0x’0y’0z’0 (рис. 4):
Рисунок 4 – Схема для преобразования систем координат О0x’0y’0z’0 и Оxkykzk
Переход от системы Оxkykzkк системе О0x’0y’0z’0 характеризуется перемещением на радиус начальной окружности обкаточного резца к центру инструмента и углом скрещивания Σ.
Матрица Mk0′ прямого преобразования:
Матрица M0′k обратного преобразования:
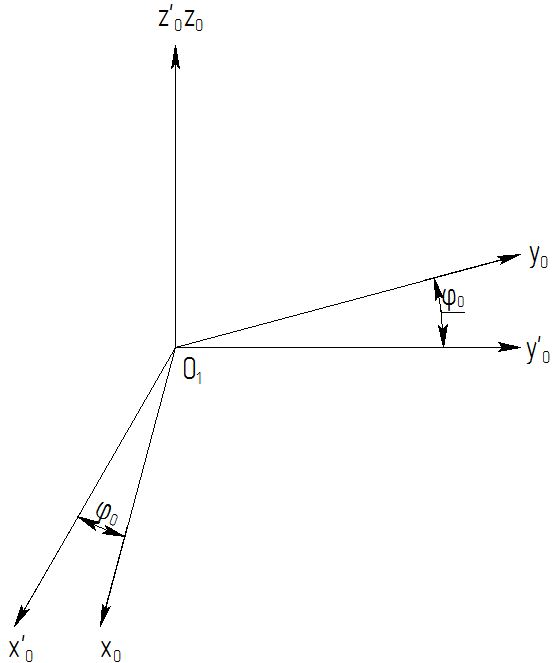
Преобразование 4: между системами О0x’0y’0z’0 и O0x0y0z0 (рис. 5):
Рисунок 5 – Схема для преобразования систем координат О0x’0y’0z’0 и O0x0y0z0
Переход от системы О0x’0y’0z’0 к системе O0x0y0z0 и обратно характеризуется поворотом на угол φ0.
Матрица M0’0 прямого преобразования:
Матрица M00′ обратного преобразования: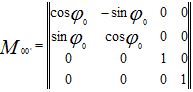
Для реализации такой кинематической схемы в работе [22] были модернизированы универсальные зубофрезерные станки, так как до модернизации станки не позволяли выполнить условия соотношения скоростей (скорость вращения стола была очень мала).
В настоящее время оборудование с ручным управлением, рассчитанное на быстрое вращение стола в РФ и за рубежом не производится. Наиболее перспективным представляется использование современных многокоординатных станков с ЧПУ, которые обеспечивают не только высокую скорость вращения стола, но и позволяют устанавливать инструмент относительно обрабатываемой детали в требуемом положении. Так же необходимо отметить, что соотношения скоростей вращения обрабатываемой детали и обкаточного резца на таком оборудовании реализуются на программном уровне.
Таким образом, соотношение скоростей определяется передаточным числом в соответствии с описанным выше соотношением ![]() . Это означает, что, если принять n1 за частоту вращения обрабатываемой детали, то частота вращения обкаточного резца составит
. Это означает, что, если принять n1 за частоту вращения обрабатываемой детали, то частота вращения обкаточного резца составит ![]() .
.
В дальнейшем, для вывода уравнения огибающей профиля обрабатываемого колеса нам понадобится результирующая матрица MS.
При этом запишем угол поворота обкаточного резца φ0, как произведение передаточного числа u0 и угла поворота обрабатываемого колеса φ1:
Аналогично считается обратная результирующая матрица MR:
В дальнейшем, полученные математические преобразования будут использоваться при выводе уравнения боковой поверхности зубьев зубчатого колеса в системе O0x0y0z0, жестко связанной с обкаточным резцом, уравнение поверхности, огибающей боковую поверхность зуба цилиндрического зубчатого колеса, и уравнения режущей кромки зуба обкаточного резца. На основе определения указанных выше уравнений строится методика профилирования обкаточного резца для нарезания зубчатых колес внутреннего зацепления методом зуботочения.
Библиографический список
- Петухов, Ю.Е. Формообразование численными методами / Ю.Е. Петухов. – М. : «Янус-К», 2004. – 200 с.
- Гречишников, В.А. Математическое моделирование в инструментальном производстве / В.А. Гречишников, Н.В. Колесов, Ю.Е. Петухов. – М. : МГТУ «СТАНКИН». УМО АМ, 2003. – 116 с.
- Петухов, Ю.Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства : дис. … докт. техн. наук : 05.03.01 / Ю.Е. Петухов. – М., 2004. – 393 с.
- Петухов, Ю.Е. Численные модели режущего инструмента для обработки сложных поверхностей / Ю.Е. Петухов, Н.В. Колесов // Вестник машиностроения. – 2003. – №5. – С. 61-63.
- Петухов, Ю.Е. Профилирование режущих инструментов среде Т-flex CAD-3D / Ю.Е. Петухов // Вестник машиностроения. – 2003. – №8. – С. 67-70.
- Петухов, Ю.Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Ю.Е. Петухов, П.В. Домнин // Вестник МГТУ «СТАНКИН». – 2011. – №3. – С. 102-106.
- Колесов, Н.В. Система контроля сложных кромок режущих инструментов / Н.В. Колесов, Ю.Е. Петухов // ИТО: Инструмент. Технология. Оборудование. – 2003. – №2. – С. 42-45.
- Петухов, Ю.Е. Компьютерная модель формообразования сложной поверхности / Ю.Е. Петухов, П.В. Домнин // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т. : сб. науч. ст. – Тула, 2010. – Т. 1. – С. 197-200.
- Колесов, Н.В. Компьютерная модель дисковых фасонных затылованных фрез / Н.В. Колесов, Ю.Е. Петухов, А.В. Баринов // Вестник машиностроения. – 1999. – №6. – С. 57-61.
- Домнин, П.В. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений / П.В. Домнин, Ю.Е. Петухов // Справочник. Инженерный журнал с приложением. – 2011. – №11. – С. 26-29.
- Колесов, Н.В. Математическая модель червячной фрезы с протуберанцем / Н.В. Колесов, Ю.Е. Петухов // СТИН. – 1995. – №6. – С. 26-29.
- Колесов, Н.В. Два типа компьютерных моделей режущего инструмента / Н.В. Колесов, Ю.Е. Петухов // СТИН. – 2007. – №8. – С. 23-26.
- Петухов, Ю.Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю.Е. Петухов, П.В. Домнин // СТИН. – 2011 – №7. – С. 14-17.
- Петухов, Ю.Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2012. – №3. – С. 28-32.
- Петухов, Ю.Е. Некоторые направления развития САПР режущего инструмента / Ю.Е. Петухов // СТИН. – 2003. – №8. – С. 26-30.
- Петухов, Ю.Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2014. – №1 (28). – С. 39-43.
- Petukhov, Y.E. Shaping precision in machining a screw surface / Y.E. Petukhov, P.V. Domnin // Russian Engineering Research. – 2011. – T. 31. – №10. – С. 1013-1015.
- Kolesov, N.V. Computer models of cutting tools / N.V. Kolesov, Y.E. Petukhov // Russian Engineering Research. – 2007. – T. 27. – №11. – С. 812-814.
- Petukhov, Y.E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y.E. Petukhov, A.V. Movsesyan // Russian Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.
- Петухов Ю.Е. Cпособ шлифования фасонных валов. Патент на изобретение RUS 863310 04.05.1979
- Цвис Ю.В. Профилирование режущего обкатного инструмента. М.: МАШГИЗ, 1961. – 156с.
- Волков Н.Н. Исследование и разработка инструмента для нарезания цилиндрических зубчатых колес с внутренними зубьями по методу зуботочения.: Дис. канд. тех. наук. – М., 1981. – 222с.