Рассмотрим методы идентификации и обработки экспериментальных данных, связанные с разработкой композиционных материалов со специальными свойствами. Неизвестные параметры оцениваются на основе сравнения значений их функциональных и структурных характеристик (устанавливаются экспериментально и/или по результатам моделирования), что дает возможность определять поправки к первоначальным значениям параметров и добиться требуемой точности оценки неизвестных параметров методом последовательных приближений [2,3].
С математической точки зрения кинетические процессы во многих дисперсных системах могут быть описаны дифференциальным уравнением второго порядка
(
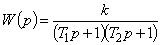). При анализе таких кинетических процессов необходимо учитывать не только скорость изменения контролируемого параметра, но как минимум и ускорение.
В отклонениях от равновесного состояния x = xm здесь будем иметь:
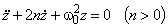. (1)
Пусть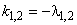 
– корни характеристического уравнения 
.
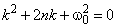При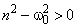 
имеем
,
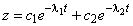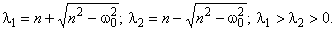
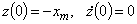с учетом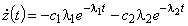 
будем иметь
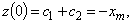
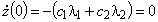.Откуда
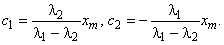
Тогда
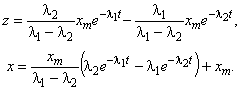(2)
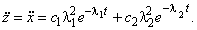
Из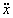 
= 0 следует
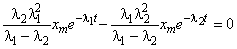.Откуда
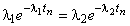,или
.
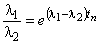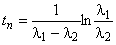(3)Займемся определением 1 и 2 по экспериментально полученному виду
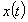. Так как 2 < 1 , то в (2) составляющая 
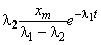затухает быстрее, чем аналогичная составляющая, соответствующая корню 2. Поэтому значение 2 можно определить по концу экспериментально полученного процесса 
.Без ограничения общности рассуждений можно принять xm = 1 (равносильно масштабированию
).В силу предыдущего
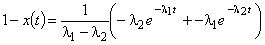.(4)Определим значение t1 такое, чтобы при t > t1 выполнялось
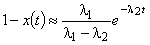.Должны иметь
, 
, 
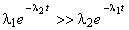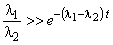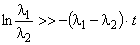.Откуда
, 
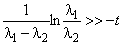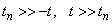.Таким образом,
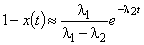, t>>tn.Введем
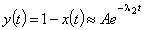.Тогда
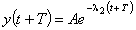.Откуда
; 
, 
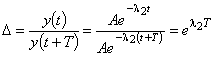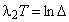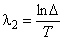.Из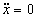 
следует
, 
;
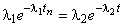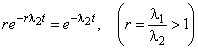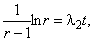
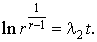
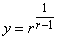.(5)Введем
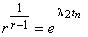.Имеем
,
, 
;
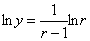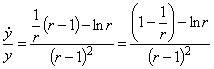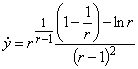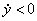при 
.Справедливо
) 
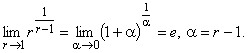
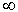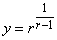не превышает e. Поэтому уравнение (5) имеет решение 
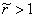лишь при 
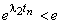.Откуда следует
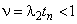, и 2 должно удовлетворять условию 
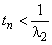. При этом 
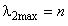(тогда 
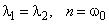).Из (3) следует
; 
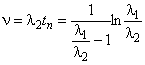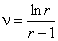.Из
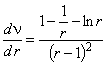<0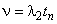
с ростом r уменьшается.Отметим,
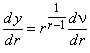.График функции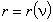 
, полученный аппроксимацией табличных значений решений уравнения (5) при различных 
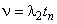методом наименьших квадратов, приводится на рис. 1.
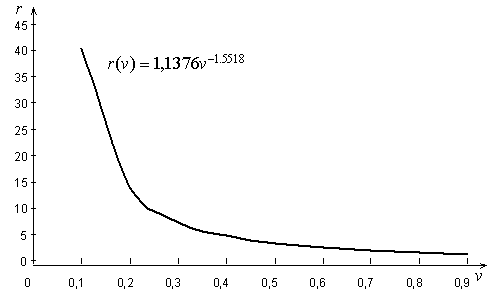Рис.1. Вид функции r = r(ν)
Найдем зависимость корней 1, 2 (определяют вид кинетического процесса) от параметров модели 0 и n (определяют упругие и демпфирующие свойства материала).
Из
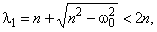
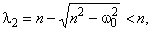
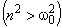
следует
.
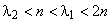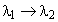при 
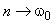.Справедливо
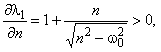
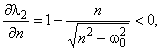
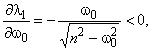
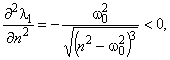
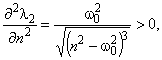
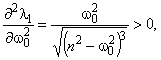
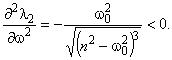
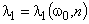и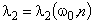 
приводится на рис.2.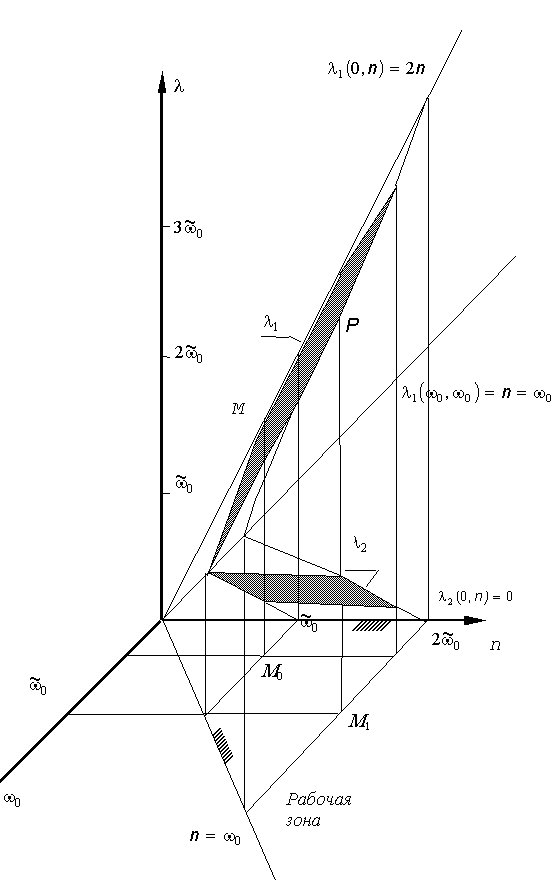
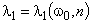и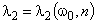 
, 
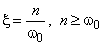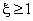. Его величина определяется структурой и физико-химическими свойствами материала.Имеем
=
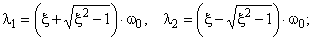
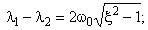
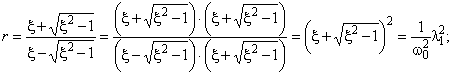
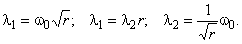
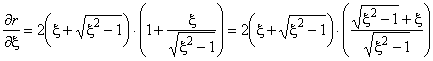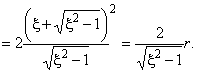
Откуда следует
.
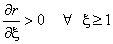Как видим, с ростом значение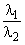 
растет.
Предложенный подход эффективно использовался при разработке композиционных материалов специального назначения и анализе других сложных систем [1,4…6].
Библиографический список
- Данилов А.М., Гарькина И.А. Сложные системы: идентификация, синтез, управление: монография. – Пенза: ПГУАС. – 2011. – 308 с.
- Данилов А.М., Гарькина И.А. Современная общая методология идентификации систем: моделирование свойств материалов / Региональная архитектура и строительство. – 2010. – №1 (8). – С.11-14.
- Будылина Е.А., Гарькина И.А., Данилов А.М. Декомпозиция динамических систем в приложениях / Региональная архитектура и строительство. – 2013. – № 3. – С. 95-100.
- Гарькина И.А., Данилов А.М., Королев Е.В. Математическое и компьютерное моделирование при синтезе строительных композитов: состояние и перспективы / Региональная архитектура и строительство. – 2010. – № 2. – С. 9-13.
- Сорокин Д.С., Данилов А.М. Методика оптимизации структуры и свойств композиционных материалов // Современные научные исследования и инновации. – Май 2014. – № 5[Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/05/34828
- Будылина Е.А., Мурачев Е.Г., Гарькина И.А., Данилов А.М. Решения уравнения клейна ‒ гордона типа бегущей волны, сглаживающейся на бесконечности // Фундаментальные исследования. – 2014. – № 5 (часть 5). – С. 1000-1005.