Актуальность темы обусловлена растущим интересом к применению методов моделирования структурными уравнениями в психологии [1,2], педагогике [3-6] и других социо-гуманитарных науках [7-12]. В связи с бурным развитием информационных технологий произошел значительный скачок в развитии не только математических методов анализа данных, но и соответствующего программного обеспечения [13-16].

В настоящей работе показана эффективность метода моделирования латентных изменений (Latent Growth Curve Modeling) в лонгитюдных (панельных) исследованиях. Гибкость этого метода в сочетании с объектно-ориентрованным интерфейсом программы AMOS SPSS позволяет оперативно корректировать модели, усложнять их, добавляя новые переменные, с целью более адекватного представления данных, и оценивать их качество.

Метод моделирования латентных изменений (далее ММЛИ) отличается от традиционных методов анализа продольных данных (L-Пейджа, χ²-Фридмана, дисперсионный анализ и т.д.) по ряду преимуществ:

а) возможность оперировать не только наблюдаемыми переменными, но и ненаблюдаемыми, т.е. латентными;

б) возможность моделировать сложные явления;

в) учет погрешности измерений;

г) возможность проверки модели на соответствие исходным данным [17].

Также эти метод, в отличие от традиционных, делает акцент не только на анализе групповых изменений, но и на индивидуальных изменениях с течением времени, а также межличностных различиях в отдельных срезах.

Цель статьи: рассмотреть особенности и преимущества применения ММЛИ в лонгитюдных исследованиях с помощью программы AMOS SPSS.

Объектно-ориентрованный интерфейс программы AMOS SPSS, позволяет трансформировать модели без обращения к сложным матричным вычислениям, что, однако, не отменяет наличия определенного уровня информационно-математической компетентности у исследователя: знания основ математической статистики (среднее, дисперсия и т.д.) и традиционных методов анализа данных (корреляция, регрессия, факторный анализ и т.д.) [18-24]. В отличие от факторного анализа, где латентные факторы операционализируются на основе наблюдаемых переменных и степень их идентификации зависит от факторных нагрузок [25, 26], в ММЛИ используются два других типа переменных:

Intercept – параметр обозначающий начальный уровень какого-либо признака (или Начало).

Slope – параметр обозначающий изменение уровня какого-либо признака с течением заданных периодов времени (или Наклон).

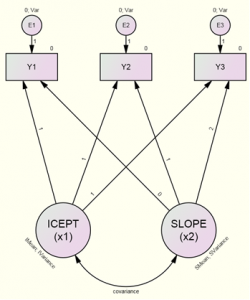
Модель линейных латентных изменений для трех временных срезов может быть представлена как с помощью модуля AMOS (см. рис.1.), так и в матричном виде (см. формулы 1 и 2).

Рис. 1. Модель латентных изменений для трех срезов

 Параметры модели могут быть описаны в общем виде:

у = Δx + e

где у – вектор наблюдаемых переменных в каждом срезе; Δ – матрица фиксированных коэффициентов нагрузок представляющих время; x – вектор скрытых факторов; e – вектор остатков.

Для любого наблюдаемого признака модель имеет два латентных фактора, которые представляют траекторию изменений: 1. ICEPT x1 (Начало) – исходный уровень признака в начале исследования. 2. SLOPE x2 (Наклон) – изменение признака за указанный период времени. Индивидуальные траектории изменений оцениваются на основе вектора x. Расширенная модель с тремя временными срезами представлена в уравнении:

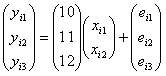
Таким образом, мы видим, что, в отличие от структурного моделирования, факторные нагрузки в ММЛИ не только имеют фиксированные значения, но и могут устанавливаться исследователем в зависимости от временных интервалов между сборами данных. Факторные нагрузки от Начала (ICEPT) к наблюдаемым переменным y_i устанавливаются равными 1, что означает одинаковое влияние фактора на показатели всех наблюдаемых срезов. Факторные нагрузки от Наклона (SLOPE) к наблюдаемым переменным y_i устанавливаются пропорционально времени между срезами, начиная с нуля. На рис.1 были установлены равные временные интервалы: Δ_i = 0, 1, 2.

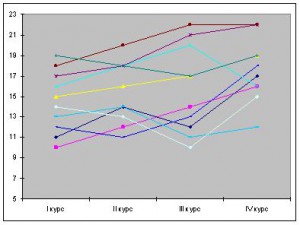
Рассмотрим наглядный пример. Исследователем были получены данные эмпатических способностей студентов за 4 года их обучения в вузе, и им была выдвинута гипотеза о том, что будет происходить линейный рост этих способностей из года в год (см. табл.1 и рис.2).

Таблица 1

Результаты эмпатических способностей студентов за 4 года обучения

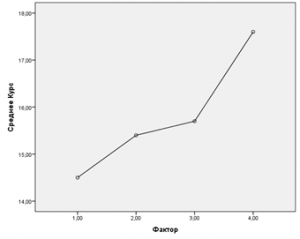
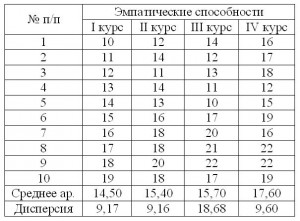На графике 2 у большинства студентов произошли изменения в показателях эмпатических способностей в положительную сторону. На графике средних значений это показано нагляднее (см. рис.3)

Рис. 2. Динамика эмпатических способностей студентов в течение 4-х лет обучения в вузе

Рис. 3. График средних значений

Статистический анализ данных с помощью дисперсионного анализа не позволил выявить значимых различий между выборками (F = 1,459; p = 0,242). В качестве причины здесь может быть небольшой объем выборки и как следствие отсутствие нормального распределения в данных, а также большая внутригрупповая дисперсия. Статистически значимая динамика была получена в результате применения непараметрического критерия L-Пейджа (L = 275,5; p < 0,01). В результате были подтверждены статистически значимые изменения в показателях эмпатических способностей студентов.

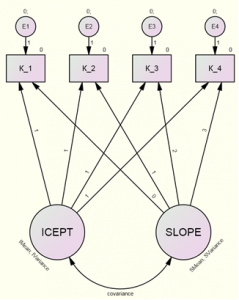
Решим эту же задачу с помощью ММЛИ. Модель для четырех временных срезов представили с помощью модуля AMOS (см. рис.4.).

Рис.4. Модель латентных изменений для четырех срезов

Отметим, что в программе AMOS можно построить исходную модель, не прибегая к использованию панели инструментов, а вызвать ее автоматически через верхнее раскрывающееся меню Plugins > Growth Curve Model и задать нужное число срезов.

Временные интервалы между срезами в этой задаче равны и составляют 1 год: начальный параметр оценивается как ноль и является базовым, 1 – это наблюдение через 1 год (II курс), 2 – через 2 года (III курс), 3 – через 3 года (IV курс).

В отличие от факторного анализа, в ММЛИ интерпретируются не факторные нагрузки, а средние значения и дисперсии Начала (ICEPT) и Наклона (SLOPE), а также ковариация между ними. Для проверки соответствия модели данным чаще всего используются индексы пригодности: критерий хи-квадрат, сравнительный индекс CFI и ошибка аппроксимации RMSEA.

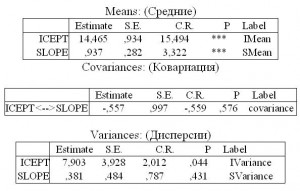
В программе AMOS все полученные результаты можно вывести нажатием клавиши F10, с помощью панели инструментов нажав на кнопку View Text или через верхнее меню View > Text Output. Результаты, полученные после обработки, отражены в таблице 2.

Таблица 2

Выходные данные 

В таблице Means среднее значение Начала (ICEPT) равно 14,465 (p < 0,001) и  это говорит, о том, что начальное (базовое) среднее значение статистически значимо отличается от нуля. Наиболее важная характеристика, Наклон (SLOPE), равна 0,937 (p < 0,001). Это значение показывает, что в среднем показатели студентов увеличиваются на 0,937 единиц в год (или скорость изменения ≈ 1 балл/год).

В таблице Variances дисперсия Начала (ICEPT) равна 7,903 (p = 0,04 < 0,05). Это означает, что на первом курсе между показателями студентов существуют значимые индивидуальные различия. Дисперсия Наклона (SLOPE), равна 0,381 (p = 0,431 > 0,05). Значит, скорость изменчивости показателей студентов составляет 0,381 единицы в год, однако этот результат статистически не значим.

В таблице Covariances между Началом (ICEPT) и Наклоном (SLOPE) ковариация равна -0,557 (p = 0,576 > 0,05) и статистически не значима. В случае статистической значимости мы бы интерпретировали результат двумя способами:

1) положительная значимая ковариация – чем выше показатель имел студент в начале обучения, тем с большей скоростью изменятся его показатели эмпатии за 4 среза.

2) отрицательная значимая ковариация – низкую скорость в изменении показателей, как правило, имели студены с более низким исходным уровнем эмпатии.

Проверка модели на соответствие исходным данным,  как и в структурном моделировании, осуществляется с использованием многочисленных индексов соответствия, которые оценивают величину расхождения между исходными данными и тем, что предсказывает модель. В ММЛИ чаще всего применяют критерий правдоподобия χ², сравнительный индекс согласия CFI и ошибку аппроксимации RMSEA. Для детального ознакомления с особенностями применения индексов в ММЛИ следует обратиться к литературе, например [8].

В исходном примере получили следующие результаты: χ² = 1,812 (p < 0,107); CFI = 0,856; RMSEA = 0,144. Уровень значимости 0,107 для критерия правдоподобия χ² больше 0,05, что говорит о хорошем согласии данных с моделью. CFI < 0,9 и RMSEA > 0,1 – отсутствие согласия данных с моделью. Следовательно, исходя из полученных индексов, мы можем сделать вывод о неудовлетворительном согласии исходных данных с предложено моделью. В таких случаях модель нуждается в коррекции: увеличении объема выборки, изменении числа срезов, усложнении или упрощении модели и т.д [27-31].

Таким образом, возможность установить значимую изменчивость среди наблюдений через скорость изменения – одно из важных преимуществ ММЛИ перед другими методами. Например, исследователь, в случае обнаружения значимого межгруппового фактора в лонгитюдном исследовании, может выявить изменения с течением времени, но ничего не может сказать об изменчивости внутри отдельной группы. В ММЛИ определив скорость изменения среднего и изменчивости, исследователь может дополнительно включать дополнительные экзогенные переменные, которые могли бы объяснить эту ​изменчивость.

1. Митина О.В. Моделирование латентных изменений с помощью структурных уравнений // Экспериментальная психология. 2008. №1. – C. 131-148.
2. Остапенко Р.И. Структурные связи ценностных ориентаций и поведенческого стиля в конфликтной ситуации работников организации [Электронный ресурс] // Перспективы науки и образования. 2013. №1. – URL: http://pnojournal.wordpress.com/archive/(дата обращения: 18.12.2013).
3. Остапенко Р.И., Остапенко А.И. Использование методов моделирования структурными уравнениями в области управления образованием [Электронный ресурс]// Государственный советник, 2013. №4. URL: http://госсоветник.рф (дата обращения: 27.12.2013).
4. Остапенко Р.И. Структурное моделирование в психологии и педагогике [Электронный ресурс] // Перспективы науки и образования, 2013. № 2. URL: http://pnojournal.wordpress.com/archive (дата обращения: 18.12.2013).
5. Остапенко Р.И. Структурное моделирование в науке и образовании: краткий обзор и перспективы развития // Современные научные исследования и инновации. – Сентябрь 2013. – № 9 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2013/09/26311 (дата обращения: 28.12.2013).
6. Остапенко Р.И. Краткий обзор и перспективы развития методов структурного моделирования в отечественной науке и практике // Перспективы науки и образования, 2013. – №5. [Электронный ресурс]. URL: http://pnojournal.wordpress.com/archive/ (дата обращения: 18.12.2013)
7. Curran, P.J., Muthén, B.: The application of latent curve analysis to testing developmental theories in intervention research. Am. J. Community Psychol. 27, 567-595 (1999)
8. DeRoche K.K. (2009) The Functioning of Global Fit Statistics in Latent Growth Curve Modeling:UniversityofNorthern Colorado. 308 p.
9. Duncan, T.E.,Duncan,S.C., Strycker,L.A.: An Introduction to Latent Variable Growth Curve Modeling. Concepts, Issues and Applications, 2nd edn.LawrenceEarlbaum, Mahwah (2006)
10. Muthén, B.: Latent variable modeling with longitudinal and multilevel data. Sociol. Method. 27, 453-480 (1997)
11. Muthén, B.: Beyond SEM: general latent variable modeling. Behaviormetrika 29(1), 81-117 (2002)
12. Preacher K.J., Wichman A.L., MacCallum R.C., Briggs N.E. Latent Growth Curve Modeling. Series: Quantitative Applications in the Social Sciences. Volume 157. 2008. 112 p.
13. Остапенко Р.И. Основы структурного моделирования в психологии и педагогике: учебно-методическое пособие для студентов психолого-педагогического факультета. – Воронеж., 2012. – 116 с.
14. Наследов А. Д. IBM SPSS Statistics 20 и AMOS. Профессиональный статистический анализ данных. – СПб: Питер, 2013. – 416 с.
15. Kline (2005) Principles and Practice of Structural Equation Modeling. (2nd Edition)GuilfordPress.
16. Schumacker, Randall E. A Beginner’s Guide to Structural Equation Modeling / Randall E. Schumacker, Richard G. Lomax. – 2^nd ed.,Lawrence Erlbaum Associates, 2004. 519 p.
17. Voelcle M.C. Latent growth curve modeling as an integrative approach to the analysis of change // Psychology Science, Volume 49, 2007 (4), p. 375-414
18. Остапенко Р.И. Формирование информационно-математической компетентности студентов гуманитарных специальностей: методические аспекты // Перспективы науки и образования, 2013. – №4. [Электронный ресурс]. URL: http://pnojournal.wordpress.com/archive/ (дата обращения: 18.12.2013)
19. Остапенко Р.И. Формирование математической компетентности студентов-психологов в условиях самодиагностики по курсу «Математические основы психологии» // Перспективы науки и образования, 2013. – №6. [Электронный ресурс]. URL: http://pnojournal.wordpress.com/archive/ (дата обращения: 18.12.2013).
20. Остапенко Р.И. Самодиагностика как условие формирования математической компетентности студентов психологических специальностей // Современные научные исследования и инновации. – Октябрь 2013. – № 10 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2013/10/28172 (дата обращения: 27.12.2013).
21. Остапенко Р.И. Методические аспекты формирования информационно-математической компетентности студентов гуманитарных специальностей // Современные научные исследования и инновации. – Май 2013. – № 5 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2013/05/24148 (дата обращения: 27.12.2013).
22. Остапенко Р.И. О корректности применения количественных методов в психолого-педагогических исследованиях // Перспективы науки и образования, 2013. – №3. [Электронный ресурс]. URL: http://pnojournal.wordpress.com/archive/ (дата обращения: 18.12.2013)
23. Остапенко Р.И. Использование структурных уравнений в моделировании процессов управления образованием // Управление образованием: теория и практика, 2013. №4. С.1-9.
24. Остапенко Р.И. Формирование математической компетентности будущих педагогов-психологов: Дис. …канд. пед. наук. [Текст] / Р. И. Остапенко. – Воронеж, 2009 – 199 с.
25. Остапенко Р.И. Латентное в социо-гуманитарном знании: понятие и классификация [Электронный ресурс] // Современные научные исследования и инновации. – Июль 2012. – № 7 – URL: http://web.snauka.ru/ issues/2012/07/15845 (дата обращения: 19.12.2014).
26. Bollen, K. (2002). Latent Variables in Psychology and the Social Sciences. Annual Review of Psychology, 53, 605-634.
27. Reinecke J., Seddig D. Growth mixture models in longitudinal research. AStA Advances in Statistical Analysis. Volume 95, Issue 4, pp.415-434. DOI: 10.1007/s10182-011-0171-4
28. Rao, C.R.: Some statistical methods for comparison of growth curves. Biometrics 14, 1-17 (1958)
29. Tucker, L.R.: Determination of parameters of a functional relation by factor analysis. Psychometrika 23, 19-23 (1958)
30. Welch G.W. Model Fit and Interpretation of Non-Linear Latent Growth Curve Models.UniversityofPittsburgh, 2007. 94 p.
31. Willet, J.B., Sayer, A.G.: Using covariance structure analysis to detect correlates and predictors of individual change over time. Psychol. Bull. 116(2), 363-381 (1994)

Все статьи автора «Остапенко Роман Иванович»