Основные предложения по модификации проективной геометрии изложены в предыдущих публикациях [2, 3, 4, 5, 6, 7] . в этой статье будет рассмотрена инцидентность двух нечетких точек, инцидентность нечеткой точки и нечеткой прямой, инцидентность двух нечетких прямых.
Две точки, две прямые, точка и прямая в двухмерном пространстве в проективной геометрии находятся в некотором связи, которую принято выражать словами инцидентность или принадлежность [9]. Инцидентность в классической проективной геометрии имеет два значения, 0 (нет) и 1 (да). Например, если расстояние между точками равно нулю, то инцидентность двух точек равна 1(да), во всех остальных случаях инцидентность равна 0(нет).
Взаимосвязь нечетких элементов в двухмерном пространстве, так же обозначается термином, инцидентность или совпадение в нечетком смысле. Однако в отличие от классического случая степень инцидентности может принимать любые значения в интервале [0;1].

Инцидентность нечетких точек на плоскости.

Опр. Назовем мерой инцидентности двух собственных нечетких точек на плоскости величину.
,           (1)
где  функция принадлежности нечеткому множеству
 функция принадлежности нечеткому множеству

Опр.. Две нечеткие точки на плоскости назовем 
инцидентными, если  и 
неинцидентными, если 

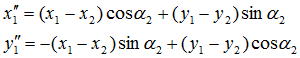Даны две нечеткие двумерные собственные точки  и  (рис. 2). С точкой  связана система координат , с точкой связана система . С помощью формул преобразования координат подсчитаем координаты математического ожидания  в системе координат  (рис. 2.)

.       (2)

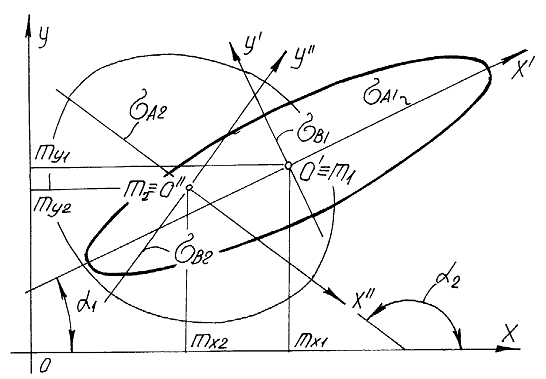
Рис. 1. Определение меры инцидентности пары двухмерных нечетких точек

Рис. 2. Координаты математического ожидания  в системе координат 

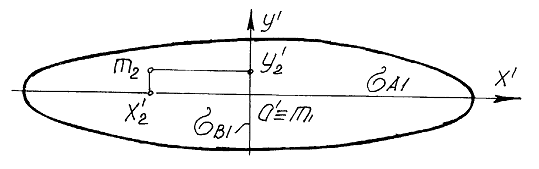
Рис. 3. Координаты математического ожидания  в системе координат 

Определим координаты математического ожидания  в системе координат (рис. 3.)
. …. (3)
Подсчитаем меру инцидентности по формуле полученной в статье [4]
,        (4)
с учетом (2) и (3)
        (5)
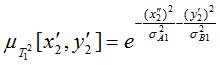      (6)
Учитывая, что  
где  - расстояние между математическими ожиданиями нечетких точек. Подставим (5),(6) в (1) с учетом  и получим формулу для подсчета инцидентности двух точек
.          (7)
Для определения инцидентности двух нечетких несобственных точек , учитывая их одномерность, равно
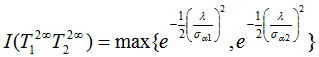      (8)
где  - тангенс угла между математическими ожиданиями несобственных точек
          (9)

Инцидентность нечетких точки и прямой на плоскости.

Опр. Нечеткую точку и прямая на плоскости назовем 
инцидентными, если  и 
неинцидентными, если 

Существует четыре варианта задачи инцидентности точки и прямой. Первый – точка и прямая несобственные. Второй – точка несобственная, прямая собственная. Третий – точка собственная прямая несобственная. Четвертый – точка и прямая собственные. 
В первом варианте, когда точка и прямая несобственные мера инцидентности всегда равна единице, так как все несобственные точки всегда лежат на несобственной прямой. 
.            (10)
Второй вариант, когда прямая собственная точка несобственная, то задача сводится к определению меры инцидентности двух несобственных точек, заданной и бесконечно удаленной точки прямой 
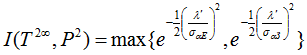         (11)
где  - тангенс угла между математическим ожиданием нечеткой несобственной точки и осью (математическим ожиданием) нечеткой прямой
        (12)
Если прямая несобственная, а точка собственная, то определяется мера инцидентности собственной и несобственной точек
        (13)
где  - расстояние математического ожидания точки от начала координат
        (14)
 – большое наперед заданное число
Даны на плоскости нечеткая точка  и нечеткая прямая  (рис. 3), надо определить инцидентность точки и прямой. Выберем две дополнительные системы координат  совпадающую с точкой и совпадающей с прямой. С помощью формул преобразования координат найдем новые координаты центра точки в системе связанной с прямой 
, (15)
Проведем прямую С через центр точки перпендикулярно оси прямой . Построим на этой прямой две одномерные точки:: -проекция нечеткой двумерной точки  на прямую С,  - перпендикулярное сечение прямой  линии С.
Среднее квадратичное отклонение точки  вычисляется по формуле 
         (16)
где  - угол между прямой С и большой осью сигма эллипса нечеткой точки
          (17)
Среднее квадратичное отклонение точки  вычисляется по формуле 
          (18)
где L – расстояние прямой  от центра нечеткой прямой .
Инцидентность двумерных точки и прямой () будет равна инцидентности двух одномерны точек () (рис. 4)
          (19)
где d –расстояние между центрами одномерных точек .

Рис. 4. Определение меры инцидентности нечетких точки и прямой на плоскости

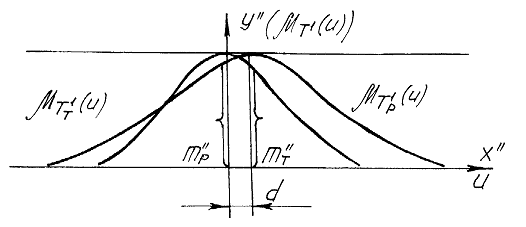
Рис. 5. Одномерные точки ,  характеризующие инцидентность нечетких точки и прямой

Инцидентность двух нечетких прямых на плоскости.
Опр. Назовем мерой инцидентности двух собственных нечетких прямых на плоскости величину.
          (20)
где  функция принадлежности нечеткому множеству
функция принадлежности нечеткому множеству
Опр. Две нечеткие прямые на плоскости назовем 
инцидентными, если  и 
неинцидентными, если 
В этой задаче можно выделить два варианта. Первый – обе прямые собственные. Второй – одна прямая собственная другая несобственная.
Даны две нечеткие прямые (рис.6)  и . С прямой  связана система координат  с прямой,  система координат . Определим координаты центра первой прямой в системе координат связанной со второй прямой  и координаты центра второй прямой в системе координат связанной с первой прямой  по формулам (2),(3). Уравнение прямой  в системе координат  будет иметь вид 
          (21)
Уравнение прямой  в системе координат имеет вид
          (22)
где , а  - угол между прямыми  и  ()

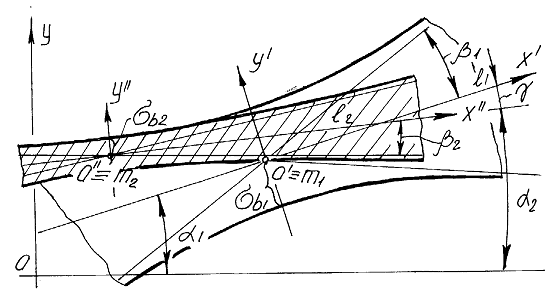
Рис. 6. Определение меры инцидентности двух нечетких прямых

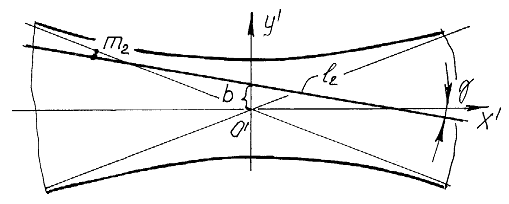
Рис.7. Уравнение прямой  в системе координат 

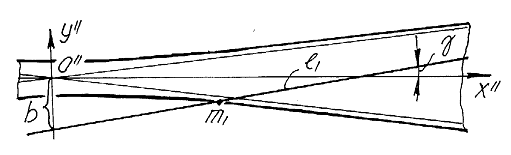
Рис. 8 Уравнение прямой  в системе координат 

Преобразуем уравнения прямых (рис. 6, рис. 7)

          (23)
Отрезок, отсекаемый прямыми от оси ординат равен
,           (24)
Уравнения назначения для элементов  и  имеет вид
          (25)
Мера инцидентности будет равна
          (26)
преобразуем выражение
          (27)
Дана нечеткая прямая . Определить ее инцидентность бесконечно удаленной прямой (рис. 8). Несобственную прямую зададим ее дополнением  - круглой точкой. Определение инцидентности собственной и несобственной прямых сводится к определению дополнения инцидентности точки и прямой. 
          (28)
Где D – расстояние между началом координат и осью прямой 
          (29)
Предложения по модификации проективной геометрии позволили разработать ряд приложений к AutoCAD позволяющих реконструировать размеры зданий по фотографиям [1] . Работа выполняется при финансовой поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности.

1. Косенков А. Ю., Марков Б. Г., Марков О. Б. Графическая реконструкция часовни Иконы Смоленской божьей матери в деревне Кинерма [Электронный ресурс] // CARELICA: научный электронный журнал.  Петрозаводск: ПетрГУ, 2013.  №1 (10). С.155–162.; URL: http://carelica.petrsu.ru/2013/Kosenkov_A.pdf. (дата обращения: 16.10.2014).
2. Марков Б. Г., Марков О. Б., Борисов А. Ю. Особенности геометрического моделирования утраченных памятников архитектуры // Ученые записки Петрозаводского государственного университета. Сер. «Естественные и технические науки.» 2013.  № 8 (137).  С. 88–92.
3. Марков Б. Г., Марков О. Б., Воронов Р. В. Модель одномерного нечеткого проективного пространства // Современные проблемы науки и образования. 2013. № 6; URL: http://www.science-education.ru/113-11542 (дата обращения: 16.10.2014).
4. Марков Б.Г., Марков О.Б. Точка в модели двумерного нечеткого проективного пространства // Современные научные исследования и инновации. 2015. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/06/56091 (дата обращения: 22.10.2015).
5. Марков Б. Г. Марков О. Б. Геометрическая интерпретация нечеткой прямой. Петрозаводск: ПетрГУ. 2003. 14 с. Деп. в ВИНИТИ 16.07.03 №1401–В2003.
6. Марков Б. Г. Марков О. Б. Геометрическая интерпретация нечеткой точки. Петрозаводск: ПетрГУ. 2003. 14 с. Деп. в ВИНИТИ 16.07.03 №1402–В2003.
7. Марков Б.Г. Прямая в модели двумерной нечеткой проективной геометрии // Современные научные исследования и инновации. 2014. № 11 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/11/40694 (дата обращения: 09.12.2014).
8. Четверухин Н. Ф. Проективная геометрия. М.: Просвещение, 1969. 368 с.

Все статьи автора «Марков Олег Борисович»