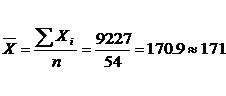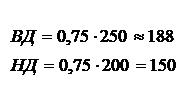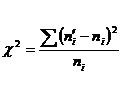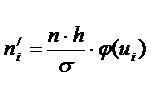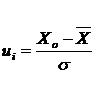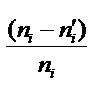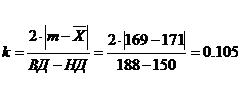Для эффективного управления качеством продукции успешно применяются методы контроля и управления качеством [1-4]. К таким инструментам можно отнести гистограммы, получившие широкое распространение из-за простоты использования и достоверности получаемой информации. Рассмотрим пример построения гистограмм для прочности железобетонных изделий [5-8].

В табл. 1 представлены значения испытаний на прочность ребристых плит покрытия после ТВО, изготовленных в теплый период года.

Таблица 1 – Результаты испытаний на прочность при сжатии

Первоначально определяем размах варьирования:

R=X_max-X_min=198-139=59

Размах варьирования делим на количество интервалов К, равный 10 и получаем ширину интервала:

Определяем частоту попадания полученных данных в соответствующий интервал и заносим эти значения в таблицу 1.

Таблица 1 – Значения частоты

Находим центр распределения:

Определяем нижний (НД) и верхний (ВД) допуски:

Центр поля допуска определяется как

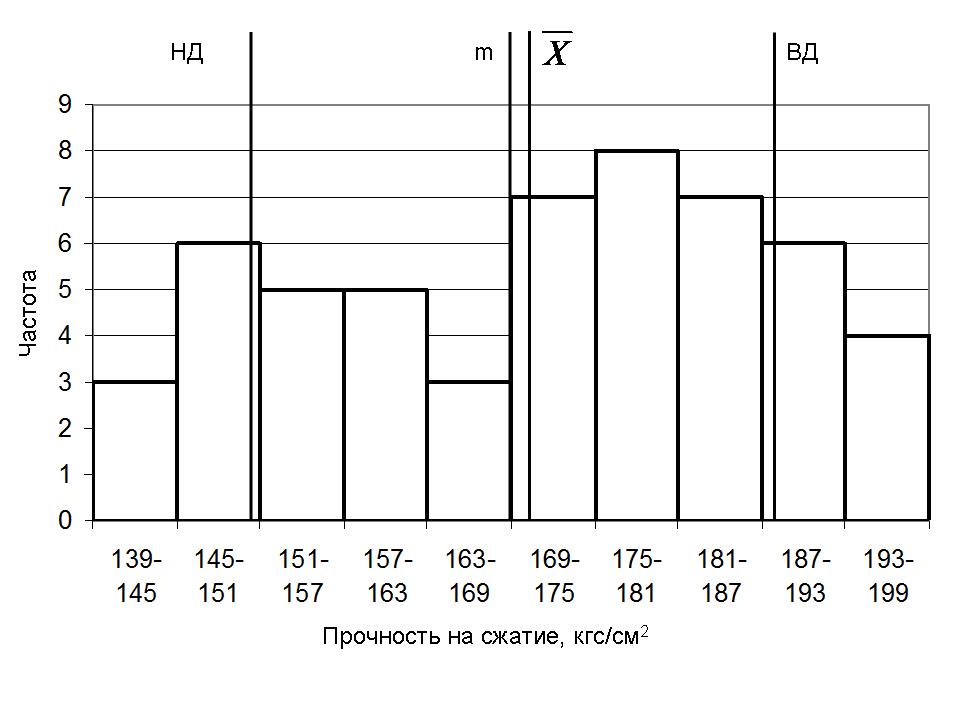
Затем строим гистограмму частот, где по оси ординат откладываем частоты, а по оси абсцисс – интервал (рис. 1)

Рисунок 1 – Гистограмма распределения прочности

Для оценки воспроизводимости процесса изготовления ребристых плит покрытия необходимо убедиться в нормальности распределения. Для того чтобы уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении, пользуются критериями согласия.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе распределения. Имеется несколько критериев согласия, но мы остановимся на рассмотрении критерия Пирсона. С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические частоты (вычисленные  в предположении нормального распределения). Критерий Пирсона показывает, значимо или незначимо расхождение между теоретическими и эмпирическими частотами.

Критерий Пирсона определяют по формуле:

Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина χ².

По таблице критических точек распределения χ² определяют в зависимости от заданного уровня значимости и числа степеней свободы k=n-3 критическую точку (α,k).

Если

то нет оснований отвергать гипотезу о нормальном распределении.

Предполагая, что генеральная совокупность распределена нормально, то теоретические частоты могут быть найдены по формуле:

где n- сумма всех частот;

h- ширина интервала;

σ – СКО;

φ(u_i) – определяется по таблице в зависимости от

где x_o-середина интервала

- среднее значение.

Вычисляем СКО:

Затем вычисляем значение u для каждого интервала(табл. 3).

Определяем по таблице функцию φ(u_i), вычисляем теоретические частоты по формуле (2) и находим χ² . Полученные результаты приведены в таблице 3.

Таблица 3 – Теоретические частоты

Интервал	Частота ni	Середина интервала Xi	ui	φ(ui)
139-145	3	142	1,8	0,0818	2	1,890914	0,630305
145-151	6	148	1,4	0,1476	3	9,412858	1,56881
151-157	5	154	1	0,2323	5	0,148639	0,029728
157-163	5	160	0,7	0,3187	6	1,770851	0,35417
163-169	3	166	0,3	0,3802	8	20,7242	6,908067
169-175	7	172	0,06	0,3982	8	0,827992	0,118285
175-181	8	178	0,43	0,3637	7	0,601208	0,075151
181-187	7	184	0,8	0,2897	6	1,550846	0,221549
187-193	6	190	1,16	0,2036	4	3,82453	0,637422
193-199	4	196	1,53	0,1238	2	2,374086	0,593522
χ2							11,13701

 Определяем число степеней свободы к=54-3=51.

Методом интерполяции находим при уровне значимости α=0,01:

Так как

то можно считать, что закон распределения нормальный

Для оценки воспроизводимости процесса рассчитаем коэффициент запаса точности технологического процесса.

Поскольку центр распределения и центр поля допуска не совпадают, необходимо воспользоваться показателем , который вычисляется по формуле

где

Вычисляем

С_pk <1 – процесс не воспроизводим.

Данная гистограмма говорит о том, что технологический процесс производства ребристых плит покрытия следует считать невоспроизводимым. Поэтому необходимо предусмотреть корректирующие действия, которые должны выполняться руководством предприятия.

Рассчитать процент брака можно по формуле

Р=Ф(λ₁)+ Ф(λ₂)

Т.к. браком будет считаться только та продукция, которая имеет значения прочности, выходящие за нижний предел, то в нашем случае формула приобретает вид Р=Ф(λ₁), где

По таблице определяем: Р=Ф(1,29)=0,4015; 0,5-0,4015=0,0985. Таким образом, количество бракованной продукции составляет 9,85%.

1. Козицына А.В., Макарова Л.В., Тарасов Р.В. Инструменты качества как эффективный способ повышения уровня качества продукции // Современные научные исследования и инновации. – Апрель 2014. – № 4 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33360 (дата обращения: 09.04.2014).
2. Козицына А.В. Инструменты повышения уровня качества и конкурентоспособности продукции [Текст] / А.В. Козицына, Л.В. Макарова, Р.В. Тарасов //Вестник магистратуры.-2014.-№ 5(32).-С.76-80.
3. Логанина, В.И. Квалиметрия и управление качеством / В.И. Логанина, Л.В. Макарова, Р.В. Тарасов // Учебное пособие.- Пенза: ПГУАС, 2014.-304с.
4. Логанина, В.И. Обеспечение качества и повышение конкурентоспособности строительной продукции [Текст] : монография / В.И. Логанина, Л.В. Макарова, Р.В. Тарасов.- Пенза: ПГУАС, 2014.-176 с.
5. ГОСТ Р 50779.10–2000 (ИСО 3534.1-93). Статистические методы. Вероятность и основы статистики. Термины и определения.
6. ГОСТ Р 50779.11–2000 (ИСО 3534.2-93). Статистические методы. Статистическое управление качеством. Термины и определения.
7. ГОСТ Р 50779.30–95. Статистически методы. Общие требования.
8. ГОСТ Р 50779.44–2001. Статистические методы. Показатели возможностей процессов. Основные методы расчета.

Все статьи автора «Макарова Людмила Викторовна»