Введение. Одним из наиболее ответственных сопряжений в сборных многоэтажных каркасах является стык ригеля с колонной. В зависимости от его конструктивного решения выполняется классификация конструктивной схемы здания и формируется расчетная схема каркаса здания. Важность этого элемента подтверждает и большое количество экспериментальных и теоретических исследований, направленных на изучение податливости стыков и связанного с этим перераспределения усилий в несущей системе каркасного здания. Объемы исследований определяются многообразием конструктивных решений, применяемых в типовых сериях каркасных зданий.
Известно, что с точки зрения работы рамы воспринимающей значительные нагрузки предпочтительны жесткие узлы сопряжений ее ригелей с колоннами. Благодаря своей способности передавать изгибающие моменты от ригеля к ригелю, жесткие узлы вовлекают в работу колонны, не загруженные поперечной нагрузкой непосредственно, что способствует уменьшению максимальных (расчетных) усилий в загруженных стержнях и вследствие этого во многих случаях удешевляет каркас здания. Кроме того, жесткие узлы повышают жесткость рамы в целом, что особенно важно при наличии горизонтальной нагрузки на раму и при увеличении этажности рамных каркасов.
Одна из особенностей сборных железобетонных каркасов зданий состоит в повышенной податливости соединений (стыков) между отдельными сборными элементами. Тем не менее, узлы в расчетных схемах сборных железобетонных рам при практических расчетах, выполняющихся по рекомендациям к типовым сериям до настоящего времени остаются главным образом двух типов — либо абсолютно жесткими, либо шарнирными, хотя анализ их работы показывает, что они не являются ни теми, ни другими.
Исследования показывают, что почти все конструкции стыков сборных железобетонных стержней имеют конечную жесткость. Это обусловлено некоторым обмятием бетона в узле, деформацией арматуры, закладных и монтажных деталей, сварных швов, неточностью монтажа, концентрацией напряжений в различных точках узла и многими другими факторами.
Под податливостью стыка понимается повышенная деформативность соединения на малом, по отношению к высоте сечения, участке длины стыка по сравнению с деформативностью самих элементов. По физической сути податливость соединения равна смещению, вызванному единичной силой – при сжатии-растяжении, сдвигу или повороту
Жесткость стыкового соединения принято оценивать по величине угла податливости-ф, на которое повернется опорное сечение ригеля, относительно колонны под действием изгибающего момента Сф=М/ φ . Среднее значение жесткости стыка при изгибе определяется как тангенс угла наклона секущей на диаграмме «М – φ»
Предварительные расчеты показывают, что коэффициент жесткости стыкового соединения оказывает заметное влияние на перераспределение усилий в элементах каркаса.
Задача исследования – сбор необходимых данных и результатов для разработки методики расчета каркасных зданий, которая позволяла бы учитывать степень податливости жесткого стыка колонны и ригеля. Задача делится на следующие подзадачи:
- Формирование расчетных моделей стыковых соединений для реализации расчетов методом конечных элементов с использованием вычислительных программных комплексов. Основное требование к моделям – максимальный учет особенностей работы стыков под нагрузкой, в том числе учет вклада податливости швов омоноличивания, сварных швов, закладных деталей и др. в общую картину напряженно-деформированного состояния стыков.
- Получить и проанализировать результаты расчетов, законы изменения коэффициента жестокости стыка в зависимости от действия нагрузок, при необходимости – модифицировать численную модель для более полного соответствия экспериментальным материалам.
- Формирование окончательных результатов расчетов – диаграмм изменения коэффициентов жесткости стыков в зависимости от расчетных нагрузок.
- Использование диаграмм для пошаговой корректировки жесткости стыков при расчетах каркасов зданий.
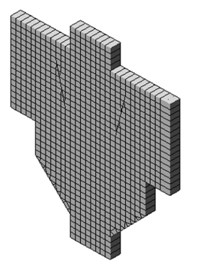
Модель стыкового соединения. В качестве рассматриваемого примера жесткого стыка выбран рамный стык по типовой серии ИИ22-1, в котором жесткость и прочность обеспечивают 3 арматурных стержня, закладная деталь на консоли колонны и бетон замоноличивания швов. Класс бетона омоноличивания принимается равным классу бетона ригеля в соответствии с требованиями серии. Модель представляет собой срез-пластину фиксированной толщины в плоскости стыка ригеля с колонной. Модель – пластина включает приопорную часть колонны с консолями, стык омоноличивания, арматурные стержни (воспринимающие опорный момент), внешнюю нагрузку в виде опорного момента ригеля. Таким образом, имеется плоская задача с тремя степенями свободы (X, Z , Uy). Пластина разделяется на прямоугольные конечные элементы размером 5см, а арматурные стержни – стержневыми КЭ.
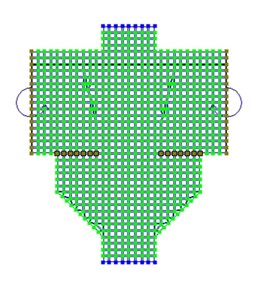 Рис.1 Конечно элементная модель жесткого стыка
Рис.1 Конечно элементная модель жесткого стыка
Рис.2 Пространственная модель жесткого стыка рамного каркаса
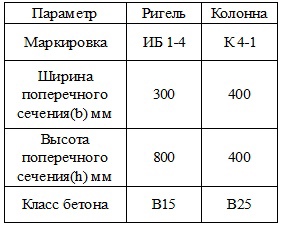
Жесткости для ригеля и колонны задаются согласно требованиям типовой серии, смотри табл.1. Толщину модели-пластины назначим 100мм. Характер работы для бетона замоноличания швов и арматуры определяется с учетом диаграмм деформирования бетона и стали, учитывающих физическую нелинейность. Податливость закладной детали характеризуется жесткостными характеристиками КЭ 56, которые могут быть заданы по направлением глобальных осей X и Z и характеризуются жесткостями Rx и Rz соответственно.
Таблица 1 Жесткостные характеристики конструкций рамного каркаса
Нагрузки, как уже говорилось ранее, представляют собой сосредоточенные опорные моменты, приложенные к модели узла сопряжения. Расчет происходит выполняется шагово-иттерационным методом, с шагом 0,1 М мах. Момент при котором наступает потеря несущей способности стыка пластины определен опытным путем и равен MR=90кН*м. Но не стоит забывать, что наша пластина представляет собой лишь треть от общей толщины конструкции. Поэтому при определении жесткости Сф=М/ф наше значение М должно быть умножено на 3
Анализ полученных результатов. После того как наша модель рассчитана нам необходимо определить правильность ее работы. Прежде всего, необходимо проанализировать деформированную схему и напряжения в конечных элементах. В нашем случае мы добились правильной работы нашей модели: деформированная схема соответствует теоретическим и экспериментальным представлениям о работе стыка и распределении полей напряжений.
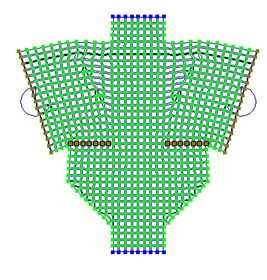
Рис.3 Деформированная модель жесткого стыка рамного каркаса.
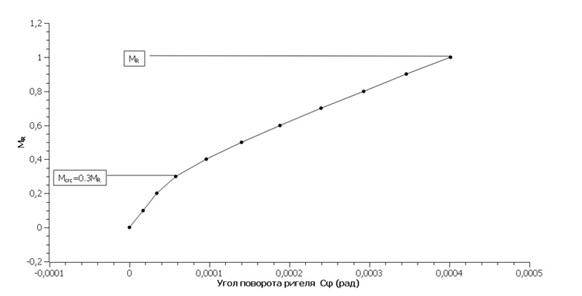
Следующая фаза анализа- это работа с диаграммой зависимости М-ф рис.4 и значением жесткости стыка Сф в момент разрушения стыка. Диаграмма зависимости М-ф нашего численного эксперимента визуально напоминает диаграммы физических экспериментов. Так же, как и в реальных экспериментах трещинообразование начинается при Мcrc=0.3МR. Еще одним свидетельством положительного результата является небольшая разность между значением Сф, полученного в момент разрушения стыка- MR, полученного нами и полученного экспериментально Быченковом, Мусатовым и Тябликовым при физическом испытании подобного стыка. Величина жесткости, при котором наступило разрушения стыка, составляет Сф=350 х106 Н*м/рад. Результат, полученный нами равен Сф=673.3 х106 Н*м/рад. Стоит отметить, что при всей схожести, есть некоторое отличие исходных данных. Речь идет о высоте поперечного сечения ригеля. Ригель который испытывала ученая группа имел высоту поперечного сечения 500мм против высоты нашего в 800мм.
Для определения угла поворота ф мы пользуемся такими параметрами как Δs и Δz. Высота поперечного сечения в этой схеме не влияет на эти перемещения, однако меньшая высота ригеля при тех же перемещениях образует больший угол ф, и в результате получаем меньшую жесткость. Аналитическим методом мы установили величину жесткости Сф для нашего эксперимента, если бы наш ригель имел подобную высоту сечения, Сф=417 х106 Н*м/рад. Разница между физическим и численным экспериментами состаила 15%.
Рис. 4 График зависимости М-ф
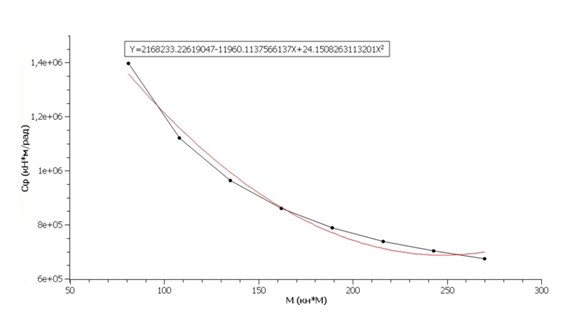
Теперь, когда нашу модель можно считать рабочей, а полученные результаты верными, настало время интегрировать Сф в расчетную схему сборного каркаса. Результатами нашей работы являются диаграммы М-ф рис. 4; Cф-М рис. 5.
Рис. 5 График зависимости Сф-М
Таблица 2 Исходные данные для построения диаграмм М-ф, Сф-м

Зависимость жесткости стыкового соединения от величины изгибающего момента. Назначение жесткости стыкам в расчетной схеме сборного каркаса.
Прежде чем продолжать описывать наш эксперимент стоит сказать немного о том , что он будет представлять в общем. Начнем с того что мы имеем каркас, к ригелям которого приложена равномерно распределенная нагрузка, которая в течении эксперимента остается неизменной. Сопряжения ригелей и колонн на первом этапе являются абсолютно жесткими. Из результатов расчета нас будут интересовать моменты в середине пролета и опорные моменты. В особенности будут интересны опорные , по их значениям будет назначаться угловая жесткость сопряжениям Сф. После назначения Сф всем интересующим нас сопряжениям, каркас будет опять рассчитываться. И так до тех пор пока разность между значениями Сф на двух последних циклах расчетов не будет ≤5%.
Итак, установим связь между Сф и М. Одним из результатов работы с нашей моделью стыка, является диаграмма зависимости Сф-М. Если внимательно посмотреть, то можно увидеть , что не хватает первых двух значений Сф и М. Мы их намеренно не включили в наш график, потому что на этом этапе угол поворота ф изменяется пропорционально изгибающему моменту. То есть на данном этапе изменялся бы только момент, а жесткость оставалась бы неизменной. На графике этот участок был бы изображен прямой линией параллельной оси изгибающих моментов. Примечательно, что ситуация меняется после начало трещинообразования. То есть жесткость стыка неизменна до начала трещинообразования и равна конкретному числу . Теперь нам надо определить закон по которому изменятся жесткость в зависимости от момента, от начала трещинообразования до потери несущей способности стыка. Определим уравнение функции по нашему графику. Итак, зависимость получена. Следующим этапом будет моделирование сборного каркаса, и анализ перераспределения моментов.
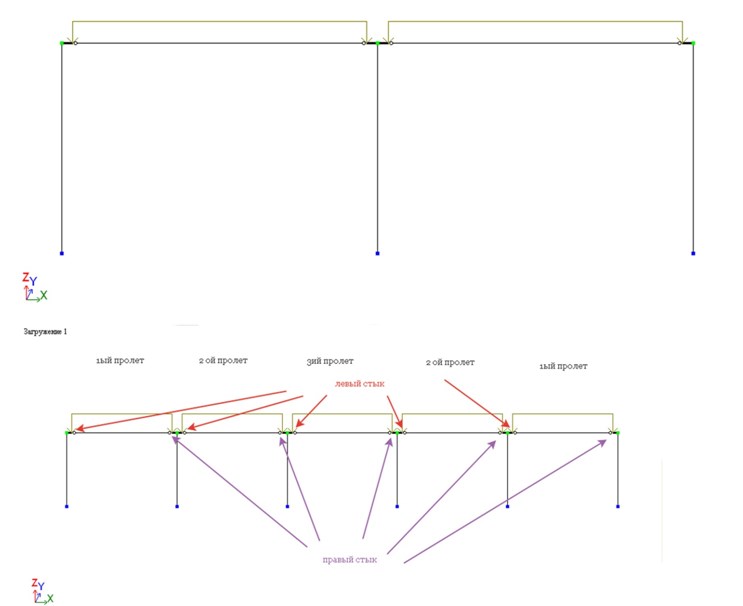
Перед началом моделирования сборного каркаса перед нами встает 2 вопроса. 1) Как назначать нашим стыкам жесткость? 2) Каким образом учитывать тело колонны? (поскольку должен быть учтен момент по грани колонны). Второй вопрос решается путем ввода жестких ставок на длину привязки колонн к осям здания. Первый вопрос решается путем ввода шарниров с сопротивлением повороту Uy которое и будет равняться жесткости наших стыков. Моделируется каркас в той же последовательности по которой мы отвечали на поставленные вопросы. Для сравнения зададим 2 схемы- 1ая двух пролетная, 2ая пяти пролетная.
Жесткости ригеля и колонны, и нагрузки на ригель назначим согласно серии, колоннам назначим жесткое защемление на опорах, длинна пролета 6м, распределенная нагрузка на ригель 30 кн/м . Анализируя результаты, мы выяснили, что изменения опорных моментов происходили в меньшую сторону и находились в диапазоне 7-10%, изменения пролетных моментов происходило в большую сторону и в крайних пролетах составило 4-5%, в центральных пролетах 13-16%.
Таблица 3. Перераспределение изгибающих и опорных моментов в 2х пролетном каркасе

Таблица 4. Перераспределение изгибающих и опорных моментов в 1ом пролете 5 пролетного каркаса

Таблица 5. Перераспределение изгибающих и опорных моментов во 2ом пролете 5 пролетного каркаса

Таблица 6. Перераспределение изгибающих и опорных моментов в 3ем пролете 5 пролетного каркаса

Библиографический список
- Абрамов Л.М. Экспериментальные исследования длительной несущей способности железобетонных рам. В кн.: Статика и динамика сложных строительных конструкций. Межвузовский тематический сборник трудов. – Л.: ЛИСИ, 1982.
- Андреев О.О. Учет податливости соединений в методе конечных элементов. – В кн.: Численные методы и алгоритмы. Труды ЦНИИСК, вып. 46.-м., 1975.
- Байков В.И., Карабанов Б.В. Анализ деформативности узлового соединения крайнего ригеля с колонной при кручении // Сб. научн. трудов / ЦНИИЭП жилища. – М., 1981. – Полносборные унифицированные конструкции в гражданском строительстве. – С. 60-68.
- Васильев А.П,, Быченков Ю.Д., Тябликов Ю.Е. Прочность стыков многоэтажных зданий при нагрузках типа сейсмических. – Бетон и железобетон, 1968, № 8.
- Васильков Б.С Володин Н.М. Расчет сборных конструкций зданий с учетом податливости соединений. М.: Стройиздат, 1985 – 144с.
- Кодыш Э.Н., Янкилевич Л.М. Совершенствование монтажа конструкций рамного каркаса. – В сб. Конструкции многоэтажных производственных зданий. – М.: ЦНИИпромзданий, 1988.
- Ларионов С.Г. Исследование прочности и жесткости перекрытий зданий павильонного типа при горизонтальных нагрузках. – Автореферат дисс. канд. техн. наук. – Воронеж, ВГАСА, 1995.
- Трекин Н.Н. Рекомендации по расчету каркасов многоэтажных зданий с учетом податливости узловых сопряжений сборных железобетонных конструкций. -ЦНИИПромзданий, Ассоциация «Железобетон», ГУПЦПП, 2002г.85с.ъ
- S. Alexander, A. Cholewicki, B. Engstrom. Structural connections for prefabricated concrete structures. FIB: Commission C6:Prefabrication, 2000.
- Zienkiewicz O.C. Cheung Y.K. The finite element method for analysis of elastic isotropic and orthotropic slabs. – Proc. I.C.E., №28, 1964.