Динамический расчёт холодильного поршневого компрессора, наравне с последующим прочностным расчётом представляют наибольшую сложность и затруднения в понимании у специалистов.
В советский период расчёт холодильного поршневого компрессора приводился в литературе под авторством следующих учёных: Розенфельд Л.М., Ткачев А.Г., Гуревич Е.С., Фотин Б.С., Пирумов И.Б., Прилуцкий И.К., Пластинин П.И., Кошкин Н.Н. и др.
Иностранная литература представлена, в основном, периодом 1980…2010 гг., поэтому из зарубежных источников можно выделить небольшое число источников, например, [1-2], в которых, однако, не приводится последовательность динамического расчёта поршневого холодильного компрессора. Следует отметить высокую публикационную активность автора Heinz P. Bloch.
Делая краткий вывод по вышесказанному, можно резюмировать, что в настоящее время информации по холодильной тематике, связанной с холодильными поршневыми компрессорами, недостаточно [3], а современные требования указывают на необходимость «свежей» литературы, не старше пяти лет. В России по холодильным компрессорам уже давно не выходили в свет новые учебные пособия, учебники, которые способствовали бы усвоению смысла и последовательности динамического анализа холодильного поршневого компрессора. Исходя из этого авторы решили привести подробную и понятную последовательность динамического анализа холодильного поршневого компрессора.
1. Исходные данные. Для расчета используем следующие данные [4]: хладагент R717; температура кипения хладагента t0 = 0 °С; температура конденсации хладагента tк = 35 °С; диаметр поршня D = 140 мм; ход поршня S = 0,126 м; степень сжатия – 3,14; температура всасываемых паров tвс = 15 °С.
На рисунке 1 показана кинематическая схема компрессора с составляющими силами и углами для динамического анализа.
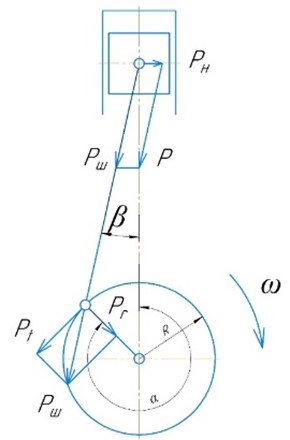
Рисунок 1 – Кинематическая схема компрессора с составляющими силами и углами для динамического анализа
Заранее следует отметить, что при проектировании холодильных компрессоров условно принято, что силы П, Iп, Rп, P (сумма П, Iп и Rп) и Pш при их положительном значении вызывают сжатие шатуна. Положительная сила Pt действует против вращения вала, положительная сила Pr действует от кривошипа к оси вращения вала.
Для расчета сил и построений графиков используем компьютерную программу MS Excell, указав в ней значения функций (таблица).
Таблица – Функции для расчета значений сил и построения графиков
| sin(α + β) / cosβ |
cos(α + β) / cosβ |
| 0,0000 |
1,0000 |
| 0,2981 |
0,9554 |
| 0,5683 |
0,8264 |
| 0,7861 |
0,6283 |
| 0,9347 |
0,3810 |
| 1,0057 |
0,1115 |
| 1,0000 |
-0,1590 |
| 0,9262 |
-0,4071 |
| 0,7975 |
-0,6190 |
| 0,6281 |
-0,7859 |
| 0,4318 |
-0,9054 |
| 0,2197 |
-0,9765 |
| 0,0000 |
-1,0000 |
| -0,2197 |
-0,9765 |
| -0,4318 |
-0,9054 |
| -0,6281 |
-0,7859 |
| -0,7975 |
-0,6190 |
| -0,9262 |
-0,4071 |
| -1,0000 |
-0,1590 |
| -1,0057 |
0,1115 |
| -0,9347 |
0,3810 |
| -0,7861 |
0,6283 |
| -0,5683 |
0,8264 |
| -0,2981 |
0,9554 |
| 0,0000 |
1,0000 |
2. Построение расчетной индикаторной диаграммы. Потери давления (депрессии) на всасывании ∆pвс и нагнетании ∆pн
для аммиачных компрессоров:
∆pвс = (0,03…0,05) p0 = 0,05 × 4,4 бар = 0,22 × 105 Па. (1)
∆pн = (0,05…0,07) pк = 0,07 × 15 бар = 1,05 × 105 Па. (2)
Сила от давления всасывания:
pвсFп = (p0 – ∆pвс) Fп = (4,4 – 0,22) × 105 × 0,015386 ≈ 6431 Н. (3)
Сила от давления кипения:
p0Fп = p0 × Fп = 4,4 × 105 × 0,015386 ≈ 6770 Н. (4)
Сила от давления конденсации:
pкFп = pк × Fп 15 × 105 × 0,015386 ≈ 23079 Н. (5)
Сила от давления нагнетания:
pнFп = (pк + ∆pн) Fп = (15 + 1,05) × 105 × 0,015386 ≈ 23694 Н. (6)
Масштаб длин:
ms = msG / msN = 1 / 1 = 1, (7)
где msG – значение длины на чертеже, мм;
msN – значение длины в натуре, мм.
Масштаб сил:
mp = mpG / mpN, мм/Н, (8)
где mpG
– значение силы на чертеже, мм;
mpN – значение силы в натуре, Н.
mp = 1 / 200 = 0,005 мм/Н.
Так, длина П на индикаторной диаграмме в масштабе составит:
17586 Н / 100 = 117,24 мм.
Величина мертвого пространства (в абсолютном выражении):
С = c0S, м, (9)
где S – ход поршня, м.
Следует отдельно отметить,
что величина вредного пространства малой и средней производительности для вертикальных компрессоров – до 1 мм, горизонтальных 1,2…2,5 мм, средней и большой производительности определяется коэффициентом c0 и может достигать больших значений.
С = 0,04 × 0,126 = 5 × 10-3 м.
Радиус кривошипа:
r = S / 2 0,126 / 2 = 6,3 × 10-2 м. (10)
Значение φ = 10…15°, примем φ = 10°.
Значение политропы сжатия для аммиачных компрессоров nc = 1,20…1,25, политропы расширения nр = 1,10…1,15. Примем nc = 1,2, nр = 1,1.
Построение политропы на индикаторной диаграмме (для сжатия ψс и расширения ψр):
(tgφ + 1)n = tgψ + 1. (11)
tgψс + 1 = (tg10° + 1)1,2; tgψс = (tg10° + 1)1,2 – 1; tgψс = 0,372;
ψс = arctg0,372 ≈ 20,4°; tgψр + 1 = (tg10° + 1)1,1; tgψр = (tg10° + 1)1,1 – 1;
tgψр = 0,196; ψр = arctg0,196 ≈ 11,1°.
Ордината точки, соответствующая давлению pн (pнFп):
y = mppiFп. (12)
y(pнFп) = 0,005 × 23694 Н = 118,47 мм; y(pкFп) = 0,005 × 23079 Н = 115,40 мм.
y(p0Fп) = 0,005 × 6770 Н = 33,85 мм; y(pвсFп) = 0,005 × 6431 Н = 32,16 мм.
Строим диаграмму по методу Брауэра [2] (рисунок 2). Это также возможно сделать по методу Брикса.
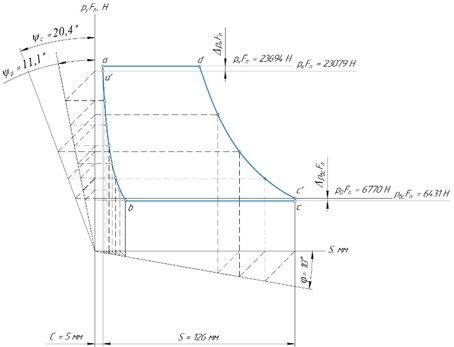
Рисунок 2 – Расчетная индикаторная диаграмма
Следует отметь, что линия сжатия c’-d на представленном выше графике не столь пологая, а линия a-d достаточно
длинна, поскольку степень сжатия составляет всего лишь 3,14; по этой причине в компрессоре достаточно, как видно из графика, около половины хода поршня для открытия нагнетательного клапана. Отсюда следует логичный вывод, что чем больше пологость политроп сжатия c’-d и расширения a-b и чем уже линии всасывания b-c и нагнетания d-a, тем больше степень сжатия компрессора и меньше период открытия всасывающего клапанов. Кроме того, при выполнении диаграммы желательно, чтобы точек, образующих адиабату сжатия, было как можно больше на диаграмме; количество точек обоих адиабат зависит так же от масштаба и углов ψс, ψр и φ. Данная диаграмма приблизительно отражает цикл поршневого холодильного компрессора.
3. Построение диаграммы суммарной силы. Отрезок от центра окружности О диаметром D, равным ходу поршня в масштабе длин, соответствующей α = 180°:
L = λrlr / 2 = 0,156 × 6,3 × 10-2 / 2 = 4,914 × 10-3 м, (13)
где λrl – отношение радиуса кривошипа к длине шатуна (λrl = 0,156);
r – радиус кривошипа, м.
Длина шатуна:
Lш = r / λrl = 0,063 / 0,156 = 0,4038 м = 403,8 мм. (14)
Масштаб длин выбирается таким же, как и на индикаторной диаграмме:
ms = msG / msN = 2 / 1 = 2.
Примем массу поршня mпорш = 2,24 кг вместе с уплотнительными и маслосъемными кольцами и поршневым пальцем, массу шатуна mш = 5,13 кг.
Масса поступательно движущейся части шатуна, сосредоточенной на оси поршневого пальца:
mш.п = 1/3 mш = 1/3 × 5,13 = 1,71 кг. (15)
Итого масса поступательно движущихся частей:
mп = mп + mш.п = 2,24 + 1,71 = 3,95 кг. (16)
Масса вращающейся части шатуна:
mвр = 2/3 mш = 2/3 × 5,13 = 3,42 кг. (17)
Угловая скорость вращения (циклическая частота) коленчатого вала (и нижней головки шатуна):
ω = 2πn = 2 × 3,14 × 16 = 100,48 рад/с. (18)
Силы инерции поступательно движущихся частей:
Iп = -mпrω2(cosα + λrlcos2α), Н, (19)
где mп – масса поступательно движущихся частей (для бескрейцкопфных машин – относят поршень и часть шатуна – 1/3 его массы), кг;
r – радиус кривошипа, м;
ω2 – угловая скорость вращения вала компрессора, рад/с;
α – угол поворота кривошипа (за начало принимается мертвая точка в начале хода поршня к валу);
λrl – отношение радиуса кривошипа к длине шатуна.
Iп = Iп1 + Iп2, Н, (20)
где Iп1, Iп2 – силы инерции первого и второго порядка, Н.
Iп1 = -mпrω2cosα, Н. (21)
Iп2 = -mврrω2λrlcos2α, Н. (22)
Силы инерции вращающихся частей:
Iвр = mврrω2, Н, (23)
где mвр – масса вращающихся частей (2/3 шатуна, масса шатунной шейки и другие неуравновешенные вращающиеся массы, приведенные к оси кривошипа), кг.
При построении диаграммы суммарной силы сила трения поступательно движущихся частей условно принимается постоянной. Значение силы трения для одного цилиндра:
![]() (24)
(24)
Мощность трения, исходя из теплового расчета:
Nтр = 82,6 × 30 = 2478 Н.
Депрессии давления на всасывании и нагнетании обычно составляют:
Δрк = Δр0 = 10 кН/м2 = 103 Па = 10-3 МПа.
Для бескрейцкопфных компрессоров:
Fк = Fв = Fп.
Суммарная сила, действующая в направлении оси цилиндра:
P = П + Iп + Rп, Н, (25)
где Rп – сила трения поступательно движущихся частей, Н.
Силы от давления газа на поршень:
П = [(pк + Δрн) × Fк] – [(pв – Δрвс) × Fв], Н, (26)
где pк, pв – давление со стороны крышки цилиндра и со стороны вала (примем равными соответственно pк и p0), Па;
Fк, Fв – площади поршня со стороны крышки и со стороны вала, м2.
П = [(15 + 1,05) × 15,39 × 10-3] – [(4,4 – 0,22) × 15,39 × 10-3] × 105 ≈ 18210 Н.
Условно силы, сжимающие шатун, считаем положительными, растягивающие – отрицательные.
Сила П меняет свое значение в зависимости от угла поворота кривошипа. Поскольку давление в картере бескрейцкопфных компрессоров равно давлению всасывания, то при развертывании индикаторной диаграммы по углу поворота кривошипа давление во всех точках уменьшается на величину, соответствующую давлению в картере.
Зависимость между углом поворота кривошипа α и перемещением поршня x:
x = r × (1+ λrl / 2 sin2α – cosα), мм, (27)
где λrl – отношение радиуса кривошипа к длине шатуна;
r – радиус кривошипа, м.
На диаграмме суммарной силы вырисовываются четыре кривые:
- сила трения, условно принятая постоянной Rп для четырех цилиндров, на графике. Знак этой силы меняется каждые 180º;
- сила давления газа на поршень П, определяется кривой, приведенной на индикаторной диаграмме;
- силы инерции поступательно движущихся частей Iп;
- суммарная сила ΣF, получающаяся при графическом суммировании всех указанных выше сил (через программу MS Excell).
Диаграмма суммарной силы приведена на рисунке 3.
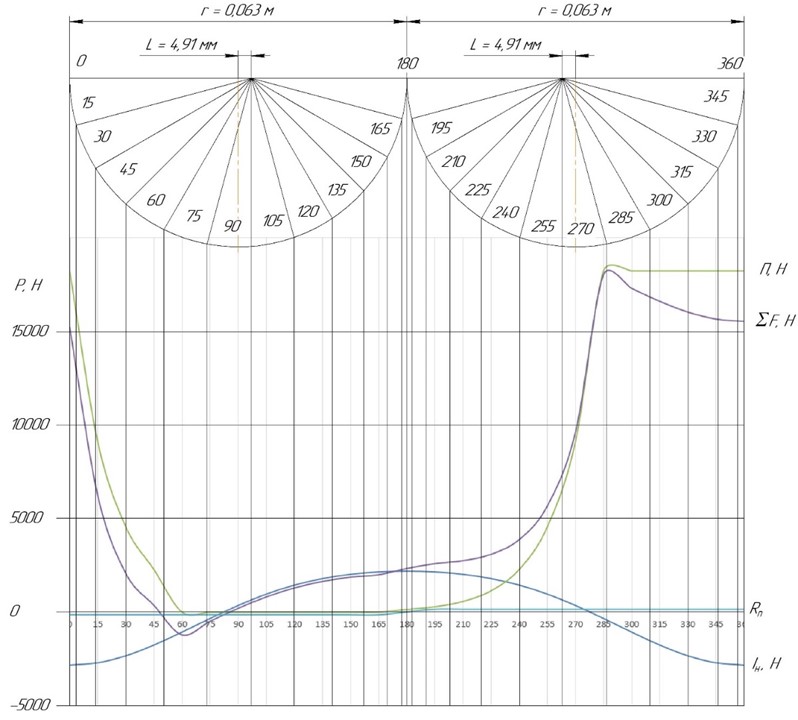
Рисунок 3 – Диаграмма суммарной силы
Из диаграммы видно, что максимальная сила сжатия составляет 18475 Н, максимальная сила растяжения составляет минус 1704 Н.
Диаграмма суммарной силы согласуется с индикаторной диаграммой по градусу повороту кривошипа и линии силы П.
Компрессоры большой степени сжатия π возможно определить по достаточно короткой линии нагнетания по сравнению с общей длиной линии, изображающей ход поршня S (менее 45º на диаграмме суммарной силы).
4. Построение диаграммы тангенциальных сил.
Тангенциальная сила, действующая на кривошип [3, 6]:
![]() (28)
(28)
Сила, действующая на стенку цилиндра (или направляющую крейцкопфа):
Pн = Ptgβ, Н. (29)
Сила, действующая по оси шатуна:
Pш = P / cosβ, Н. (30)
Значения силы P (на диаграмме ΣP) берутся из диаграммы суммарной силы для соответствующих α.
Сила трения вращающихся частей:
![]() (31)
(31)
Суммарная кривая тангенциальных сил можно рассматривать и как кривую момента, противодействующую вращения вала компрессора:
Mвр = (ΣPt + Rвр) × r, Н×м. (32)
При построении диаграммы тангенциальных сил учитываем, что угол смещения кривошипов (при четырех цилиндрах) составляет 90º.
Диаграмма тангенциальных сил представлена на рисунке 4.
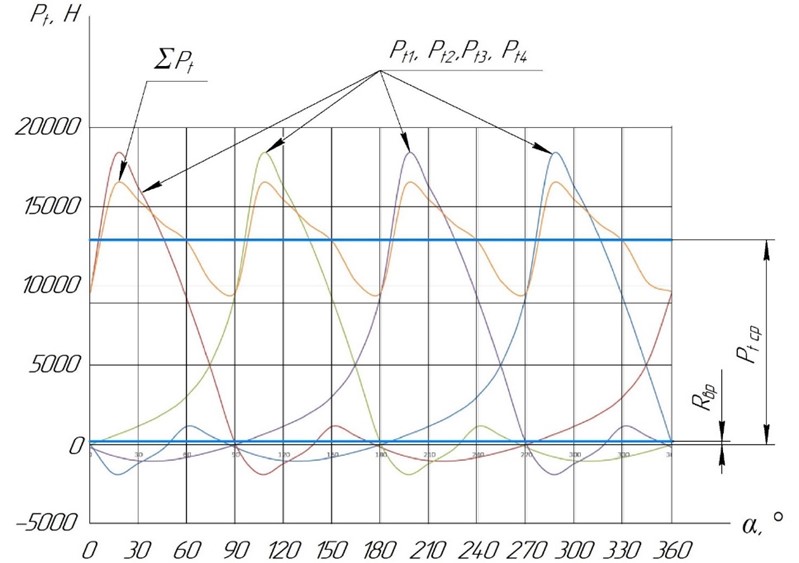
Pt ср – средняя величина тангенциальных сил; ΣPt – суммарная кривая тангенциальных сил
Рисунок 4 – Диаграмма тангенциальных сил
Максимальная суммарная тангенциальная сила ΣPt на сжатие составила 18113 Н, сила растяжения каждого Pt составляет -1165 Н.
5. Построение диаграммы радиальных сил.
Радиальная сила, действующая на кривошип:
![]() (33)
(33)
Кроме силы Pr в радиальном направлении на кривошип действуют постоянные силы инерции вращающихся масс.
mш.вр = 2/3 mш = 2/3 × 5,13 = 3,42 кг. (34)
Масса части шатунной шейки, приходящейся на один шатун:
![]() (35)
(35)
где dш.ш – диаметр шатунной шейки (примем равной 0,102 м), м;
lш.ш – длина шатунной шейки (примем равным 0,085 м), м;
ρ – плотность материала коленчатого вала, кг/м3.
![]()
Сила инерции от вращающейся части шатуна:
Iш.вр = mш.врrω2 = 3,42 × 0,063 × 100,482 ≈ 2175 Н. (36)
Сила инерции от массы части шатунной шейки, приходящейся на один шатун:
Iш.ш = mш.шrω2 = 2,56 × 0,063 × 100,482 ≈ 1628 Н. (37)
Силы инерции Iвр.ш и Iш.ш действуют от оси вращения вала, т.е. являются отрицательными.
На кривошипный (шатунный) подшипник действует сумма сил:
Pr‘ = Pr – Iш.вр, Н. (38)
На вал компрессора действует сумма сил:
Pr” = Pr – (Iш.вр + Iш.ш), Н. (39)
На рисунке 5 показана диаграмма радиальных сил.
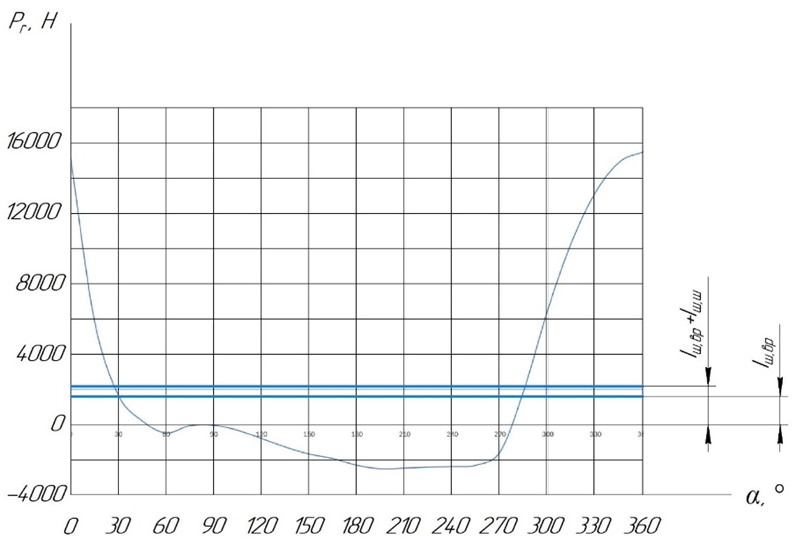
Рисунок 5 – Диаграмма радиальных сил
Максимальная радиальная сила составила: Pr = 15513 Н; Pr’ = 13338 Н; Pr” = 11710 Н.
6. Уравновешивание. Чтобы компенсировать действие сил инерции, нужно применять многорядную компоновку и противовесы. Используем четырехрядную компоновку с двумя коленами (шатунными шейками) вала под углом 180°, угол между рядами – 90°. При данной компоновке силы инерции первого порядка взаимно уравновешены, силы инерции второго порядка не уравновешивают [1-2].
Результирующая сил инерции второго порядка, действующая по горизонтали:
Iп2 = 2√2 mпrω2λcos2α, Н, (40)
где mп – масса противовеса, кг.
Силы инерции неуравновешенных вращающихся масс взаимно уравновешены.
Момент сил инерции первого порядка, действующий в плоскости колен, постоянный по величине при всех положениях вала:
M1 = mпrω2a, Н×м. (41)
где a – расстояние между серединами колен, м;
b – расстояние между противовесами, м.
Этот момент может быть уравновешен двумя противовесами с массой, приведенной к радиусу кривошипа:
![]() (42)
(42)
где mп – масса поступательно движущихся частей, кг.
Момент сил инерции второго порядка равен нулю.
Масса противовеса, приведенная к радиусу кривошипа:
![]() (43)
(43)
где V0 – объем противовеса, м3;
ρ – плотность материала противовеса, кг/м3;
rпр – расстояние от центра массы противовеса до оси вращения, м.
![]()
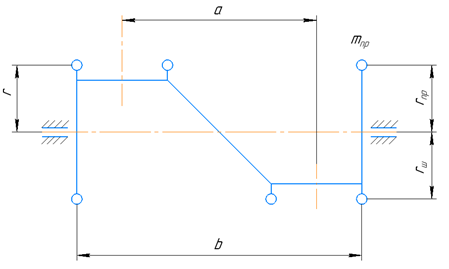
Рисунок 6 – Схема к расчету уравновешивания
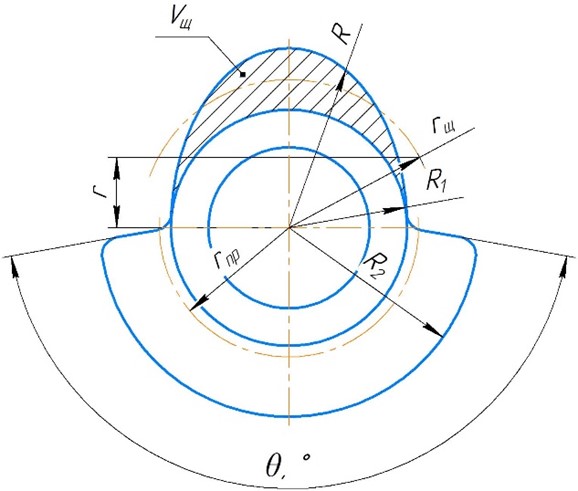
Рисунок 7 – Схема к расчету противовесов
Масса неуравновешенной части щеки:
mщ = Vщρ = 1,785 × 10-4 × 7850 = 1,4 кг, (44)
где Vщ – объем неуравновешенной части щеки, м3.
Полная величина неуравновешенной части щеки:
![]() (45)
(45)
где i – число шатунов на шатунной шейке, шт.;
mш.ш – масса части шатунной шейки, приходящейся на один шатун, кг;
rщ – радиус инерции щеки;
mщ – масса неуравновешенной части щеки, кг;
r – радиус кривошипа, м;
mш.вр – масса вращающейся части шатуна, кг.
![]()
Приведенная масса противовеса, уравновешивающая момент сил инерции неуравновешенных вращающихся масса:
![]() (46)
(46)
Полная приведенная масса противовеса:
![]() (47)
(47)
Масса противовеса:
![]() (48)
(48)
где rпр – приведенный радиус инерции противовеса, который определяется по принимаемым размерам противовеса известными методами механики, м.
Угол габарита противовеса:
![]() (49)
(49)
где hср – средняя толщина противовеса, м.
Сила инерции противовеса:
Iпр = mпрrпрω2 = 11,60 × 0,074 × 100,482 ≈ 8667 Н. (50)
Сила инерции неуравновешенной части щеки:
Iщ = mщrщω2 = 1,4 × 0,08 × 100,482 ≈ 1136 Н. (51)
7. Расчет маховика. Окружная скорость обода (не должна быть выше 30…40 м/с для чугунных и 100 м/с – для стальных маховиков):
vоб = rнω, м/с, (52)
где rн – радиус обода, м;
Максимальная избыточная работа:
![]() (53)
(53)
где fmax – площадь наибольшей избыточной площадки на диаграмме тангенциальных сил, мм2;
mх – масштаб длин, мм/м;
mр – масштаб сил, мм/Н.
![]() (54)
(54)
Требуемый момент инерции маховика:
![]() (55)
(55)
где δ – допускаемая степень неравномерности вращения вала компрессора (δ≤1/30…1/40 – при ременной передаче, δ≤1/80 – при соединении муфтой, δ≤1/8…1/10 – при частичной нагрузке).
Достаточная для обеспечения допускаемой степени неравномерности масса муфты:
![]() (56)
(56)
где rи – радиус инерции муфты, м.
Степень неравномерности вращения муфты при ее массе 25 кг:
![]() (57)
(57)
vоб = 0,15 × 100,48 = 15,07 м/с.
Таким образом, рассмотрена особенности и структурированная последовательность выполнения расчетов для построения диаграмм тангенциальных сил и радиальных сил, расчета противовесов и маховика, выполняемых при проектировании холодильного поршневого компрессора.
Таким образом, рассмотрена рассмотрены особенности и структурированная последовательность выполнения расчетов для построения индикаторной диаграммы и диаграммы суммарных сил, производимых при проектировании холодильного поршневого компрессора.
Библиографический список
-
Heinz P. Bloch Fluid Machinery: Life Extension of Pumps, Gas Compressors and Drivers / Heinz P. Bloch. – Walter de Gruyter GmbH, 2020. – 208 p.
-
Heinz P. Bloch Petrochemical Machinery Insights / Heinz P. Bloch. – Butterworth-Heinemann, 2016. – 784 p.
-
Щерба В.Е. Теория, расчет и конструирование поршневых компрессоров объемного действия / В.Е. Щерба. – М.: Юрайт, 2019. – 324 с.
-
Сязин И.Е., Касьянов Г.И., Гукасян А.В. Особенности теплового расчета поршневого холодильного компрессора // Холодильная техника. – № 12. – 2019. – С. 30-33.
