Введение
В современной теории сигналов [1] де-факто исходят из того, что процедуры дискретизации и восстановления сигнала выполняются в одной и той же инерциальной системе отсчета (ИСО). В то же время с точки зрения специальной теории относительности (СТО), постановка задачи восстановления сигналов должна включать ситуацию, когда дискретизация сигнала выполняется в одной ИСО, а его восстановление в другой. В дальнейшем будем называть первую ИСО стационарной, а вторую движущейся. При этом все обозначения с апострофом (´) будут относиться к движущейся ИСО.
Согласно СТО связь между интервалами времени возникновения любого события в разных ИСО выражается преобразованием Лоренца [2]:
Δt´ = γ Δt (1)γ = 1 /![]()
где:
γ - Лоренц-фактор ( γ ≥ 1 )
![]() - скорость движущейся ИСО
- скорость движущейся ИСО
с - скорость света в вакууме
Последовательность отсчетов дискретного сигнала рассматривается ниже как ряд событий, следующих друг за другом с временным интервалом Δt и «возникающих» в той или иной ИСО.
Восстановление сигнала в движущейся ИСО
Рассмотрим сигнал с ограниченным спектром, дискретизированный с постоянным интервалом выборки в стационарной ИСО и подлежащий восстановлению в движущейся ИСО.
В соответствии с теоремой Котельникова-Шеннона (далее, теорема отсчетов) такой сигнал может быть восстановлен в соответствии с выражением [1]:
S(t)´ =![]() (2)
(2)
где:
Δt´ - интервал выборки в движущейся ИСО
Δt - интервал дискретизации в стационарной ИСО
![]() - граничная частота спектра сигнала
- граничная частота спектра сигнала
s(k) - отсчеты сигнала, сформированные в стационарной ИСО
При этом согласно теореме отсчетов интервал выборки должен удовлетворять неравенству:
Δt´ ≤ ![]() (3)
(3)
С другой стороны, на основании соотношения (1) между интервалами выборки в стационарной и движущейся ИСО можно записать
γΔt ≤ ![]() (4)
(4)
Поскольку всегда γ>1, отсюда следует:
Δt ≤ ![]() (5)
(5)
Таким образом, для безыскажающего восстановления сигнала в движущейся ИСО интервал выборки этого сигнала в стационарной ИСО должен быть уменьшен в γ раз по сравнению интервалом в случае постановки задачи, когда дискретизация и восстановление сигнала происходят в одной и той же ИСО. Заметим, что неравенство (5) соответствует релятивисткой формулировке, которая при γ=1 сводится к стандартной теореме отсчетов [3].
Пример восстановления сигнала в движущейся ИСО
Рассмотрим единичный гармонический сигнал:
E(t) = cos(2πt) (6)
Далее, в соответствии с теоремой отсчетов примем в нашем примере интервал выборки:
Δt = ![]() (7)
(7)
Тогда согласно соотношению (1):
Δt´ = ![]() (8)
(8)
В этом случае в соответствии с выражением (2) для сигнала, который должен быть восстановлен в движущейся ИСО, можно записать:
E(t)´ =![]() (9)
(9)
где:
e(k) = cos(πk/6) (10)
Результаты компьютерного моделирования восстановления сигнала (6) в соответствии с выражением (9) представлены ниже в графической форме для трех значений Лоренц-фактора (точки на графике соответствуют отдельным отсчетам).
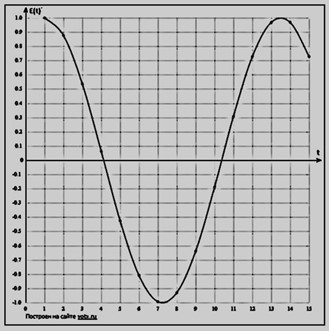
Рис.1 Восстановление гармонического сигнала при γ=1
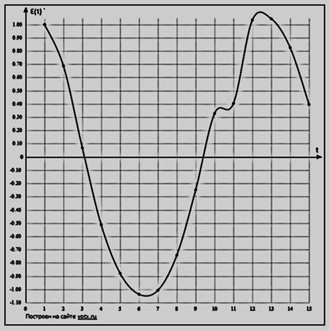
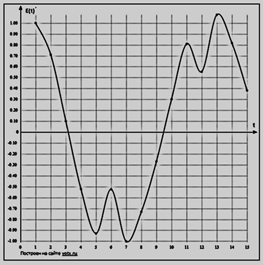
Обсуждение полученных результатов
Из вышеприведенного примера следует, что при восстановлении сигналов в движущейся ИСО могут возникать гармонические искажения, величина которых возрастает с увеличением Лоренц-фактора, если не принять меры к уменьшению интервала выборки в стационарной ИСО согласно (5) [3].
В таблице ниже представлены соответствующие значения коэффициента гармонических искажений (КГИ) в зависимости от величины Лоренц-фактора.
Таблица 1. Коэффициент гармонических искажений в зависимости от γ
|
γ
|
КГИ (%)
|
|
1,00
|
0,00
|
|
1,05
|
6,38
|
|
1,10
|
12,89
|
|
1,15
|
18,14
|
|
1,20
|
23,39
|
Таким образом, КГИ фактически зависит от скорости движущейся ИСО. Следует отметить, что на практике наиболее высокая скорость, которая была достигнута космическим аппаратом «Helios 2», составляет ≈0,0229% скорости света [4], что соответствует величине Лоренц-фактора ≈1,000000026. В вышеприведенном примере КГИ при этом оценивается на уровне ≈0,000001%. Таким образом, что касается рассмотренной постановки задачи, эти искажения в настоящее время находятся в пределах допустимой погрешности измерения.
Выводы
Рассмотрена постановка задача восстановления сигнала в движущейся ИСО по выборке отсчетов, сгенерированной в стационарной ИСО. При этом показано, что при выборе интервала дискретизации необходимо учитывать значение Лоренц-фактора, которое зависит от относительной скорости перемещения движущейся ИСО. В связи с этим предложена расширенная формулировка теоремы отсчетов. Помимо часто теоретического аспекта, рассмотренный подход может быть полезным в соответствующих приложениях, требующих особо высокой точности восстановления сигнала, или при достижении уровня техники, обеспечивающего достаточно высокие скорости космических аппаратов.
Библиографический список
- Медиченко М.П., Литвинов В.П. Радиотехнические цепи и сигналы: Учебное пособие. – М.: Изд-во МГОУ. 2011: 151 с.
- Forshaw Jeffrey, Smith Gavin. Dynamics and relativity. John Wiley & Sons: 2014: 344 p.
- Сучилин В.А. Relativistic Approach to Signals and Systems // Современные научные исследования и инновации. 2017. № 11 [Электронный ресурс] URL: http://web.snauka.ru/issues/2017/11/84761
- Книга рекордов Гиннеса // Guinness-World-Records. [Электронный ресурс] URL: http://www.guinnessworldrecords.com/world-records/66135-fastest-spacecraft-speed
