Introduction
Generally signals and systems used to be treated without taking into account effects of special relativity [1]. However, their consideration could be useful in view of the current and future space developments. According to special relativity the reference system, travelling in the homogeneous and isotropic space with a steady velocity, is defined as moving inertial reference system (IRS). At the same time the IRS of the observer is defined as stationary IRS (in relation to the moving IRS). One of the consequences of special relativity is that the clocks in the moving IRS are measured as slower than the similar clocks in the stationary IRS. This relativistic time dilation has been empirically certified by the experiment with a pair of atomic clocks while one of them was sent on the space mission [2]. The same phenomenon has been registered also through measurements of μ-meson cosmic radiation in the atmosphere [3]. It is logical to assume that the relativistic time dilation should affect all processes associated with clocking.
Next for the sake of clarity it should be agreed on appropriate symbols which will be used further. So symbols with acute accent (´) belong to the moving IRS. On the other hand, symbols without acute accent belong to the stationary IRS.
Presentation of relativistic time dilation in frequency area
By definition, the relativistic time dilation is expressed by means of the Lorentz factor [1]
γ = 1 /(1+(v/c)2)1/2 (1)
where
v – relative velocity of the IRS
c – speed of light
According to special relativity the speed of light which is the physical constant cannot be surpassed, and therefore γ > 1. So the times in both IRS are related as
t = t´ / γ (2)
From here
t < t´ (3)
that is the formal indication of the relativistic time dilation. Consider the signal in form of a simple harmonic oscillation[4]
g(t) = A cos (2π f t + φ) (4)
where
A – oscillation amplitude
f – oscillation frequency
φ - oscillation phase
Then by substituting (2) in (4) we obtain
g(t´) = A cos (2π f´t´+ φ) (5)
where
f´ = f / γ (6)
This equality describes the presentation of the time dilation in frequency area. Hence, the frequency of harmonic oscillation in the moving IRS is decreased in relation to the stationary IRS. In view of that, for instance, the GPS system has required an appropriate adjustment of on-board synthesizer to provide correct frequency for terrestrial applications [5].
Further any complex periodical signal G(t) can be presented as the sum of simple harmonic components [4] :
G(t) = ∑ An cos (2πn t fn + φn) (n= 0,∞) (7)
Next in the moving IRS, by analogy to (6) for each component (7) should be
fn´ = fn / γ (8)
Thus, the frequencies of components in (7) are decreased in the moving IRS in relation to the stationary IRS. In other words, in the consequence of relativistic time dilation the signal frequency spectrum gets the red offset.
One comment on the red offset by optical signals
A class of harmonic oscillation includes also monochromatic optical signals [6]. Thus, as shown above, they are subject to decreasing of his frequency and accordingly increasing of his wavelength in the consequence of the relativistic time dilation. In this way it can be concluded that while the velocity of propagation of optical signals (say speed of light) is the physical constant and does not depend on the choice of IRS, the frequency or wavelength of the optical signal is variable and is determined in dependence on relative velocity of the moving IRS in which this signal is produced. That means that any optical signal, which is produced in the moving IRS, will be perceived in the stationary IRS with the red offset (not confuse with the Doppler’s red shift [1]).
Relativistic generalization of Nyquist–Shannon theorem
According to Nyquist–Shannon theorem [4] the sampled signal with the spectrum limited to the Nyquist frequency fN can be correctly restored according to the sequence of its reference values, which are selected with the sampling rate interval
h < 1 / 2fN (9)
Then in the moving IRS the sampling rate interval should be taken as
h´< 1 / 2f´N , (10)
and combining (6) and (10) we obtain
h´ < γ / 2fN (11)
Thus (11) presents relativistic generalization of the Nyquist–Shannon theorem. In case of γ = 1 the inequality (11) takes form of (9) which correspond to the stationary IRS. However, in the moving IRS the sampling rate interval should be selected in accordance with (11).
Relativistic generalization of Shannon-Hartley theorem
According to Shannon-Hartley theorem [4] the channel capacity is determined as
C = fc log (1+S/N) (12)
where
fc – cut frequency (channel bandwidth)S/N – signal-to-noise ratio
It is clear that on interval (-∞,∞) the signal-to-noise ratio
SNR =ʃ |S(f)|2df / ʃ |N(f)|2df (13)
is time-invariant. Thus, the channel capacity only depends on the bandwidth.
Then in the moving IRS
C´ = f´c log (1+S/N) (14)
Since subject to (6)
f´c = fc / γ (15)
Shannon-Hartley theorem is generalized with
C´= fc /γ log (1+S/N) , (16)
and in view of (12)
C´= C/ γ (17)
Thus, in the moving IRS occurs decreasing of the channel capacity. In the case of γ = 1, equality (15) corresponds to the stationary IRS. Note this effect should be taken into account also on evaluating of the achievable maximum of the channel capacity [7].
Relativistic time dilation impact on the impulse response of a discrete system
Consider the impulse response of a discrete system as a sampled signal [8]. Then in accordance with the generalized Nyquist-Shannon theorem the appropriate clock rate interval of the discrete system with a given cut frequency fc should satisfy the inequality
η < γ / 2fc (18)
Note that the case γ = 1 in (18) corresponds to the stationary IRS. On the other hand the time dilation impact on discrete system entails an increasing of the system time response. Indeed, any part of time response of the discrete system is the sum of the clock rate intervals. But according to (18) η is increasing exactly with the factor γ. Since the whole time response can be presented as the sum of such intervals, the system time response also increases.
Relativistic time dilation impact on the system service life period
One of the ways to represent the system service life period is an appropriate modelling of the so-called bathtub-shape failure rate function [9]. For the convenience of analysis, we make of use the model presented in [10], which includes the variable T (service life period )
S(t) = β-1e-δt – (β·T ln t/T)-1 , (19)
where β and δ are specified parameters which are determined statistically.
In view of (2) in the moving IRS should be
S(t´) = β-1e-δt´/γ – γ(β·T´ ln t´/T´) (20)
where
T´= γ·T (21)
Thus in the moving IRS as opposed to the stationary IRS the system service life period increases exactly with the factor γ. This result being postulated by special relativity is confirmed here by means of the mathematical-statistical modelling.
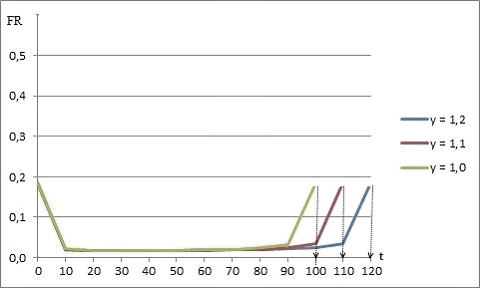
In the Fig.1, the failure rate curves and hereby the service life period (in terms of time span of the curve) are provided for some values of γ. Note the case γ = 1 corresponds to the stationary IRS.
Relativistic time dilation impact on the mean time between failures
The mean time between failures (MTBF) is an important reliability characteristic which is often presented along with the failure rate function [11]. MTBF is useful in the phase of service life period where the failure rate practically may be assumed constant (the flat part of the curve in the Fig.1). By definition, MTBF is a reverse quantity to the parameter of Poisson distribution [9]
R(t) = e-t/M (22)
where M is MTBF.
Then in the moving IRS subject to (2)
R(t´) = e-t´/M´ (23)
where
M´= γ·M (24)
Thus, in the moving IRS the mean time between failures increases exactly with the factor γ. In the case of γ = 1, equality (24) corresponds to the stationary IRS.
Discussion
The severity of exposure of relativistic time dilation depends on the value of the Lorentz factor. In turn the last one is determined by the relative velocity of the moving IRS. In the case v ≪ c the impact of relativistic time dilation is not big enough to produce simply measurable effect for application. However, the relative velocity, which approaches to 30,000 km/s (ten per cent speed of light) and more, makes the relativistic time dilation rather tangible. In the Table 1 below are shown a number of the Lorentz factor values with the according relative velocities in the percent of speed of light.
Table 1. The Lorentz factor versus relative velocity
| The Lorentz factor |
1.005
|
1.021 | 1.048 | 1.091 | 1.155 | 1.250 | 1.400 | 1.667 | 2.294 |
| Relative velocity | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% |
At present (perhaps also in the immediate future) the relative velocities shown above remain not technically feasible. However, some highly fine applications may require these effects to be taken into account also at the current stage of technological development.
Conclusions
A number of aspects of the relativistic time dilation impact on signals and systems were considered. This consideration led to generalization of the Nyquist-Shannon and Shannon-Hartley theorems. Thereupon it was shown that the time dilation impact is presented as follows:
- decrease of the oscillation frequency
- compress of the signal spectrum (red offset)
- decrease of the channel capacity
- increase of the system time response
- increase of the system service life period
- increase of the mean time between failures.
In principle, this requires an additional tuning of software or hardware, or appropriate taking these effects into account on designing. Anyway, on the actual stage of study this list should not to be considered as comprehensive. Besides, some of these effects perhaps are not confined with the framework of technology, and may occur in other systems. From this point of view a definite similarity between technical and biological systems may be also taken into account [12].
References
- Forshaw, Jeffrey; Smith, Gavin. Dynamics and Relativity. John Wiley & Sons: 2014. 344 p.
- Gott, J., Richard. Time Travel in Einstein’s Universe. Boston Mariner Book, Houghton Mifflin: 2002. 304 p.
- Frisch, D. H.; Smith, J. H. (1963). Measurement of the Relativistic Time Dilation Using μ-Mesons. American Journal of Physics. 31 (5): 342–355.
- Pierce, John R. An Introduction to Information Technology theory – Symbols, Signals and Noise (second revised edition), Dover Publications, New York, 1980. 336 p.
- Ashby, Neil. Relativity in the Global Positioning System. Living Reviews in Relativity. Department of Physics, University of Colorado, Boulder, Colorado 80309-0390 USA.
- Алешкевич В. А. Курс общей физики. Оптика. М.: Физматлит, 2011.
- Сучилин В. А. Предельно достижимая скорость одноканальной передачи данных // Современные научные исследования и инновации. 2017. № 9 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/09/84289
- Электронный учебно-методический комплекс: Теория автоматического управления. Часть 2: Дискретные, нелинейные, оптимальные и адаптивные системы /С.В.Лукьянец, А.Т.Доманов, В.П.Кузнецов, М.А.Крупская-Мн.: БГУИР, 2007. 159 с.
- Richard E. Barlow, Frank Proschan. Statistical Theory of Reliability and Life Testing. Holt, Rinehart & Winston Inc., N. Y.: 1975. 290 p.
- Soutchilin, V. A. On the Modeling of the Bathtub-Shape Failure Rate Function // Современные научные исследования и инновации. 2017. № 10 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/10/84384
- Mondro, Mitchell J. (June 2002). “Approximation of Mean Time Between Failures When a System has Periodic Maintenance”. IEEE Transactions on Reliability. 51 (2).
- Wiener, N. Cybernetics or Control and Communication in the Animal and the Machine, Mit University Press Group Ltd; Second edition: 1961. 212 p.
