Введение
Динамика гетерогенных структур с фазовыми переходами на границах играет важную роль в природных и искусственных системах [1].
Например, каждую зиму в г.Москве от сорвавшихся с крыш снеголедовых масс и сосулек страдает более 50 человек и до 300 автомобилей.
Самолеты, вертолеты, морские суда, портовые сооружения, нефтегазовые, космические объекты и др. подвержены обледенению. Эти процессы чреваты серьезными финансовыми потерями, гибелью людей.
Математическое моделирование динамики гетерогенных структур снеголедовых масс является актуальной задачей.
1. Фундаментальная модель нестационарного теплообмена
Модель описывается в рамках двухмерного нестационарного уравнения теплопроводности, граничные условия задают конвективный теплообмен с окружающей средой.
Рассматривается бесконечная структура прямоугольного сечения, составленная из разнородных материалов. Материалы различаются теплофизическими свойствами: теплопроводностью , удельной теплоемкостью С, коэффициентом теплообмена с окружающей средой ![]() . На верхних и нижней гранях происходит конвективный теплообмен с окружающей средой, температура которой
. На верхних и нижней гранях происходит конвективный теплообмен с окружающей средой, температура которой ![]() . Две другие грани теплоизолированы.
. Две другие грани теплоизолированы.
В начальный момент времени структура нагрета до температуры ![]() . Задача состоит в нахождении поля температур
. Задача состоит в нахождении поля температур ![]() .
.
В математическом отношении задача сводится к решению нестационарного уравнения теплопроводности в двухмерной области G c соответствующими краевыми и начальными условиями:
![]() ;
;
![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Здесь ![]() тепловой поток;
тепловой поток; ![]() – коэффициент теплопроводности,
– коэффициент теплопроводности, ![]() – удельная теплоемкость;
– удельная теплоемкость; ![]() – температура в момент
– температура в момент ![]() . Решение
. Решение ![]() ищется в цилиндре
ищется в цилиндре ![]() , основанием которого является прямоугольник G с границей дG.
, основанием которого является прямоугольник G с границей дG.
2. Конечно-разностная модель гетероструктуры
Задача решается методом конечных разностей, в G вводится пространственная сетка
![]()
![]()
![]()
и сетка по времени
![]() .
.
Здесь ![]() – переменные шаги сетки по пространству в направлениях Х и Y и по времени, соответственно.
– переменные шаги сетки по пространству в направлениях Х и Y и по времени, соответственно.
Задача решается на сетке ![]() , вводится сеточная функция температуры
, вводится сеточная функция температуры ![]() , определенная на
, определенная на ![]() . Разностная схема во внутренней области G записывается на крестообразном шаблоне с центром в узле
. Разностная схема во внутренней области G записывается на крестообразном шаблоне с центром в узле ![]()
На сетке ![]() рассматривается ячейка с центром в узле
рассматривается ячейка с центром в узле ![]() и вершинами в полуцелых узлах, то есть образованными пересечением прямых, проходящих через середины отрезков, соединяющих узлы шаблона, параллельно направлениям X и Y. Размеры ячейки по этим направлениям:
и вершинами в полуцелых узлах, то есть образованными пересечением прямых, проходящих через середины отрезков, соединяющих узлы шаблона, параллельно направлениям X и Y. Размеры ячейки по этим направлениям:
![]()
![]()
Площадь ячейки ![]() , разностные производные определяются
, разностные производные определяются
.gif)
.gif)
![]()
Здесь введены безиндексные обозначения для размеров ячейки и производных ![]() Вводятся также безиндексные обозначения для потоков через грани ячейки:
Вводятся также безиндексные обозначения для потоков через грани ячейки:
![]()
![]()
![]()
В соответствии с интегро-интерполяционным методом построения разностных схем уравнение теплового баланса для ячейки имеет вид:
![]() (2)
(2)
Здесь использовано обозначение ![]() ,
, ![]() .
.
Узлам, лежащим на границе дG, будут соответствовать шаблоны и ячейки несколько иного вида. Если дополнить шаблон в этих точках фиктивными узлами, то уравнение баланса в них запишется так же, требуется только положить нулевым соответствующие фиктивные шаги. В общем случае размеры ячейки будут:
.gif) (3)
(3)
где 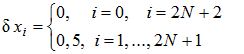 ,
, .gif) .
.
Потоки через пограничные грани ячейки определяются в случае граничного узла из краевых условий исходной задачи:
![]()
![]()
![]()
![]()
Разностная схема на сетке ![]() :
:
.gif) , (4)
, (4)
где
.gif)
.gif)
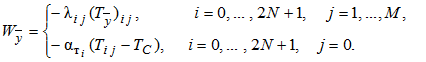
.gif)
Таким образом, на каждом временном слое ![]() получена нелинейная система алгебраических уравнений (4), в которую решение подобной системы на предыдущем слое входит как неизвестная функция. На нулевом слое задано начальное распределение:
получена нелинейная система алгебраических уравнений (4), в которую решение подобной системы на предыдущем слое входит как неизвестная функция. На нулевом слое задано начальное распределение:
![]() .
.
3. Модель организации внешнего и внутреннего итерационных процессов.
Для организации внешнего интеграционного процесса вводится вектор-функция ![]() и операторы
и операторы ![]() , определенные равенствами:
, определенные равенствами:
.gif) , тогда система (4) запишется так:
, тогда система (4) запишется так:
![]() . (5)
. (5)
Для решения ее используется линейно-квадратический процесс. Система (5) переписывается в виде: ![]()
![]()
(здесь ![]() – значение функции на верхнем временном слое), применяется линейно-квадратичный итерационный процесс:
– значение функции на верхнем временном слое), применяется линейно-квадратичный итерационный процесс:
![]() .
.
Верхним индексом помечается номер итерации. Здесь ![]() и
и ![]() линейные операторы
линейные операторы
.gif) ,
,
где например,
.gif)
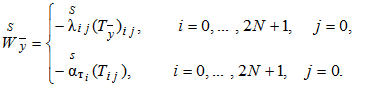
![]() .
.
Внутренний итерационный процесс организуется следующим образом. На каждой итерации внешнего процесса линейная система разностных уравнений записывается без индексов внешней итерации, вводится диагональный оператор D так, что ![]() , и в операторном виде система имеет вид:
, и в операторном виде система имеет вид:
![]() .
.
Для приближения решения этого оператора уравнения применяется двухслойная итерационная схема с чебышевским упорядоченным набором параметров
.gif) .
.
Здесь ![]() – упорядоченный чебышевский набор параметров. В пространственной сеточной функции
– упорядоченный чебышевский набор параметров. В пространственной сеточной функции ![]() в смысле некоторого скалярного произведения удовлетворяются условия самосопряженности, положительной определенности и ограниченности оператора
в смысле некоторого скалярного произведения удовлетворяются условия самосопряженности, положительной определенности и ограниченности оператора
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
гарантирующие сходимость внутреннего итерационного процесса.
Границы спектра ![]() и
и ![]() оператора
оператора ![]() эффективно оцениваются по теории Гершгорина.
эффективно оцениваются по теории Гершгорина.
4. Импульс градиента температур
Конкретные исследования по описанию алгоритму проведены для следующих значений параметров линейной задачи:
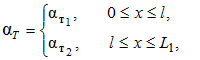
.gif)
.gif)
где ![]()
Температурное поле и характер его изменения во времени имеют общий для всех вариантов расчета характерный вид. Температура металла практически постоянна по объему, и при переходе из стали в наледь поверхности теплообмена со средой круто падает, то есть в точках наледи, лежащих на его поверхности по границе с металлом, возникает значительный градиент температуры, направленный вдоль поверхности наледи. Кривая зависимости градиента температуры в угловой точке от времени имеют характерную форму, близкую к форме импульса. Близость кривой к импульсной форме определяется величинами ![]() и
и ![]() .
.
При уменьшении ![]() и
и ![]() импульс сглаживается. Такая зависимость от
импульс сглаживается. Такая зависимость от ![]() и
и ![]() сохраняется при всех исследованных отношениях
сохраняется при всех исследованных отношениях ![]() , причем от
, причем от ![]() острота и амплитуда импульса зависят существенно сильнее, чем от
острота и амплитуда импульса зависят существенно сильнее, чем от ![]() , отношение
, отношение ![]() слабо влияют на форму зависимости и определяет преимущественно амплитуду импульса.
слабо влияют на форму зависимости и определяет преимущественно амплитуду импульса.
Градиент температуры в угловой точке достигает своего максимального значения примерно в одно и то же время (около одной секунды с начала остывания) при различных значениях ![]() из исследованных интервалов. Крутизна фронта пропорциональна его амплитуде и растет с увеличением как
из исследованных интервалов. Крутизна фронта пропорциональна его амплитуде и растет с увеличением как ![]() и
и ![]() , так и с увеличением отношения
, так и с увеличением отношения ![]() . В то же время крутизна спада слабо зависит от отношения
. В то же время крутизна спада слабо зависит от отношения ![]() и определяется главным образом значениями
и определяется главным образом значениями ![]() и
и ![]() .
.
Полученные результаты позволяют объяснить предпочтения в выборе материала кровли.
5. Модель процесса замерзания жидкого слоя
Математическое моделирование нестационарных тепловых полей состоит в решении нестационарного уравнения теплопроводности в двумерной области G с соответствующими граничными и начальными условиями:
.gif) (6)
(6)
Особенностью рассматриваемой задачи является необходимость учета фазового перехода из жидкого в твердое состояние.
Для сквозного счета таких задач без явного выделения фронта затвердевания нужно учесть, что при температуре фазового перехода ![]() энергия Е, как функция температуры, испытывает переход величины
энергия Е, как функция температуры, испытывает переход величины ![]() , который называется теплотой фазового перехода, поэтому для энергии справедливо:
, который называется теплотой фазового перехода, поэтому для энергии справедливо:
.gif) , где
, где
.gif)
Это выражение подставляется в уравнение энергии:
![]() , и учитывая что
, и учитывая что ![]()
есть дельта-функция Дирака, получается уравнение:
![]() , справедливое и в области фазового перехода. Выражение
, справедливое и в области фазового перехода. Выражение ![]() и
и ![]() входят в уравнение одинаковым образом, причем
входят в уравнение одинаковым образом, причем ![]() представляет собой сосредоточенную теплоемкость на поверхности
представляет собой сосредоточенную теплоемкость на поверхности ![]() .
.
Для перехода к разностной схеме заменяется дельта-функция приближенно – образной или размазанной функцией ![]() , где – величина полуинтервала, на котором функция
, где – величина полуинтервала, на котором функция ![]() отлична от нуля.
отлична от нуля.
Таким образом, вводится сглаженная или эффективная теплоемкость ![]() , которая удовлетворяет условию
, которая удовлетворяет условию ![]() вне интервала
вне интервала ![]() .
.
Изменение энтальпии на интервале ![]() сокращается, т.е.
сокращается, т.е.
.gif) .
.
На интервале ![]() можно, например, взять
можно, например, взять .gif) , что будет соответствовать интерполяции – функции с помощью прямоугольного импульса. На том же интервале производится сглаживание коэффициента теплопроводности . Вводится сглаженный, или, эффективный коэффициент
, что будет соответствовать интерполяции – функции с помощью прямоугольного импульса. На том же интервале производится сглаживание коэффициента теплопроводности . Вводится сглаженный, или, эффективный коэффициент ![]() , совпадающий с
, совпадающий с ![]() при
при ![]() и с
и с ![]() при
при ![]() .
.
Например, если задавалось
.gif)
То можно взять
.gif)
В результате получается задача для уравнения теплопроводности со сглаженными коэффициентами:
![]() ,
,
![]() .
.
Моделирование процессов затвердевания границ льда и основы позволяют выбрать композитные тонкие слои по границам гетероструктур [1].
Выводы
1. Рассмотрена фундаментальная модель процесса теплообмена в гетероструктуре в форме нестационарного уравнения теплопроводности.
2. Описана конечно-разностная модель гетероструктур с введением пространственной сетки и применением интегро-интерполяционного метода построения разностных схем.
3. Предложена эффективная модель организации внешнего и внутреннего итерационных процессов с применением двухслойной итерационной схемы с чебышевским упорядоченным набором параметров.
4. Модель процесса замерзания жидкого слоя наледи построена без явного выделения фронта затвердевания с учетом теплоты фазового перехода.
5. Проведены системные исследования тепловых процессов в гетероструктурах, установлены закономерности протекания нестационарных процессов.
Заключение
1. Модели динамики гетероструктур снеголедовых масс с фазовыми переходами на границах позволили установить новые закономерности нестационарных процессов обледенения наиболее распространенных в технике гетероструктур.
2. Использование установленных закономерностей в практике проектирования гетероструктур представляет новые возможности в получении более безопасных конструкций.
3. Наиболее распространенные гетероструктуры крыш зданий и сооружений целесообразно устраивать с разными коэффициентами трения точечно по всей крыше и узкой (около 1 %), полосе гидрофобного композита по краям крыш для снижения размера сосулек до безопасного. В качестве тонкослойных композитов для разных материалов крыш разработаны и испытаны эффективные, весьма долговечные и недорогие составы, а также технологии их нанесения с учетом конкретных условий применения.
Библиографический список
- Динамика гетероструктур. Фундаментальные модели. Смогунов В.В., Климинов И.П., Вдовикина О.А. и др. Пенза, Изд-во ПензГУ, 2002. – 598 с.
