Введение

В настоящей работе рассматривается процесс протекания межзвездного газа через потенциальную яму рукава спиральной галактики – задача, связанная с появлением ударных волн – так называемых галактических ударных волн (ГУВ). С точки зрения физики межзвездной среды (МЗС), для данной задачи является важным и учет самогравитации, и учет тепловых процессов, поскольку уплотнение газа за фронтом ударной волны неизбежно вызывает тепловую неустойчивость формирующихся уплотнений и их дальнейшее сжатие под действием собственной гравитации. На сегодняшний день влияние ГУВ на состояние МЗС достаточно хорошо исследовано, однако ряд вопросов, касающихся, в частности, структуры фронта ГУВ, по-прежнему остаются актуальными.

Постановка задачи и физическая модель.

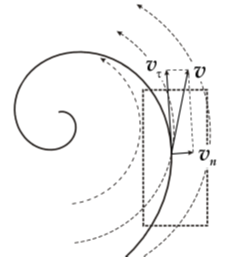
При рассмотрении данной задачи будем исследовать движение газа в плоскости галактического диска в окрестности спирального рукава, не учитывая вертикальных движений газа. Будем рассматривать лишь область течения в окрестности участка спирального рукава. Положение расчетной области показано на рисунке 1а. При таком локальном описании изменения потенциала гравитационного поля звездного диска вдоль рукава малы, т.к. градиент звездной плотности в диске ориентирован преимущественно перпендикулярно рукаву, а потому полем диска можно пренебречь.

Будем предполагать, что газ является идеальным и политропным с показателем адиабаты γ = 5/3. Влиянием вязкости и магнитных полей в рамках данной модели будем пренебрегать. С учетом слагаемых, описывающих тепловые эффекты, система уравнений газодинамики принимает следующий вид:

	(1)
	(2)
	(3)
	(4)
	(5)

где ρ – плотность газа, n – его концентрация, p – давление, v – скорость, E – полная энергия единицы объема газа, T – температура, Г = 1.6·10^-25 эрг/с — функция нагрева, Λ(T) — функция охлаждения. Вклад в гравитационное поле дает как сама потенциальная яма рукава, так и собственная гравитация газа:

	(6)
	(7)
	(8)

где f_s - сила, действующая со стороны спирального рукава, f_c - сила, действующая со стороны газа, Ψ — потенциал гравитационного поля газа, G — гравитационная постоянная.

а)	б)
Рисунок 1. Положение расчетной области относительно спирального рукава показано прямоугольником. Пунктирными стрелками обозначено направление орбитального движения газа

Будем считать, что потенциальная яма рукава первоначально отсутствует, и с течением времени ее глубина увеличивается за характерное время ф по закону:

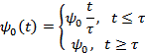(9)

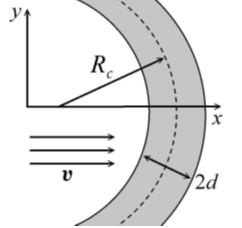
где Ψ₀ — конечная глубина ямы. Рост амплитуды потенциальной ямы можно интерпретировать, как формирование спиральной волны плотности в галактике, и выбрать для времени ее развития ф время формирования спиральной структуры – 1-2 периода обращения галактики, т.е. ~ 200-500 миллионов лет. С геометрической точки зрения потенциальная яма представляла собой участок кольца (рисунок 1б) с радиусом средней линии R_s = 10 кпк и полутолщиной d = 1 кпк. При этом распределение гравитационного поля определяется потенциалом вида:

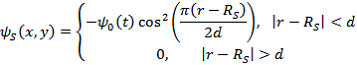(10)

где r = ((x + R_s)² + y²)^1/2 — расстояние от центра кольца до точки внутри него.

Безусловно, реальное натекание газа на спиральный рукав происходит под некоторым углом, т.е. согласно рисунку 1 обе составляющих скорости газа отличны от нуля в окрестности рукава. Однако эффекты сжатия газа и образования ГУВ связаны в первую очередь с нормальной составляющей скорости v_n, поэтому целесообразно исследовать модели с v_τ = 0.

При локальном рассмотрении задачи также можно считать распределения параметров МЗС в натекающем потоке однородными, за исключением распределения плотности (концентрации) вещества. Наличие неоднородностей в течении обусловлено тепловыми процессами и самогравитацией, поэтому необходимо учесть их при определении параметров газа на входной (левой) границе расчетной области. Распределение параметров в невозмущенном потоке на этой границе были заданы следующим образом:

	(11)
	(12)

Вариации концентрации создавались равномерно-случайно в указанном диапазоне величин (12), чтобы сымитировать неоднородность МЗС.

В качестве параметров обезразмеривания естественно использовать следующие величины:

n₀ = 0.1 см^-3 - характерная концентрация межоблачного газа,

m₀ = 1.67·10^-24 г – масса протона,

G = 6.67·10^-8 см³/с²·г – гравитационная постоянная,

d = 1 кпк – полуширина потенциальной ямы спирального рукава.

Тогда обезразмеривание гравитационного потенциала производится с помощью величины φ₀ = Gn₀m₀d ² ≈ 10¹¹ см²/с², скорости – u₀ = φ₀^1/2 ≈ 3.16·10⁵ см/с, времени – t₀ = d/u₀ ≈ 3·10⁸ лет. После обезразмеривания максимальная глубина потенциальной ямы Ψ₀ = 25, скорость натекания газа на левой границе области v_0x = 3-8, время развития потенциала ф = 1, функция нагрева Г = 9.04.

Методика расчетов и результаты

Решение данной задачи производилось численно. Следует отметить, что для наиболее качественного учета вклада собственной гравитации в динамику среды лучше всего использовать либо лагранжев подход, либо методы расчета на адаптивных сетках, поскольку при гравитационном коллапсе размеры и объем облаков МЗС уменьшаются многократно. Тем не менее, при решении астрофизических задач, в которых существенна самогравитация, успешно применяется (например, [1], [2]) и эйлеров подход с фиксированным шагом сеток.

При решении данной задачи был использован код, основанный на явной TVD-схеме второго порядка точности [3], [4], [5]. Данная схема является консервативной относительно массы, энергии и импульса газа, сохраняет интенсивность контактных разрывов и ударных волн благодаря малой численной диффузии, а также удовлетворительно воспроизводит движение облаков. Для вычисления потенциала Ψ (собственного гравитационного поля газа) был использован метод решения уравнения Пуассона (8), основанный на быстром преобразовании Фурье ([6], [7]).

При использовании эйлерова подхода в задачах с учетом самогравитации существенную роль играет выбор шага расчетной сетки. Это связано с тем, что развитие гравитационной неустойчивости сопровождается образованием конденсаций газа высокой плотности и малого масштаба. Однако фактически нижний порог масштабов при числен­ном моделировании определяется как раз шагом сетки. Поэтому вычисления следует проводить на сетках с шагом, размер которого меньше характерного масштаба формирующихся в процессе фрагментации уплотнений. В частности, для облаков HI (концентрация n~10² см^-3, температура Т~30-70 К) джинсовский масштаб составляет λ_J ~ 20-30 пк, а уже для межоблачного газа (n~0.1 см^-3, Т~10⁴ К) он существенно больше - λ_J ~ 5 кпк. Таким образом, для повышения качества решения целесообразно выбрать для сетки разрешение, близким к λ_J облаков.

Расчетная область, потенциальная яма и направление натекания газа схематически показаны на рисунке 1б. Расчетная область представляла собой квадрат со стороной 11 кпк. При вычислениях были использованы разрешения 256х256 (с шагом h≈0,043 кпк) и 512х512 (h≈0,021 кпк), сопоставимые с масштабом Джинса в облаках HI.

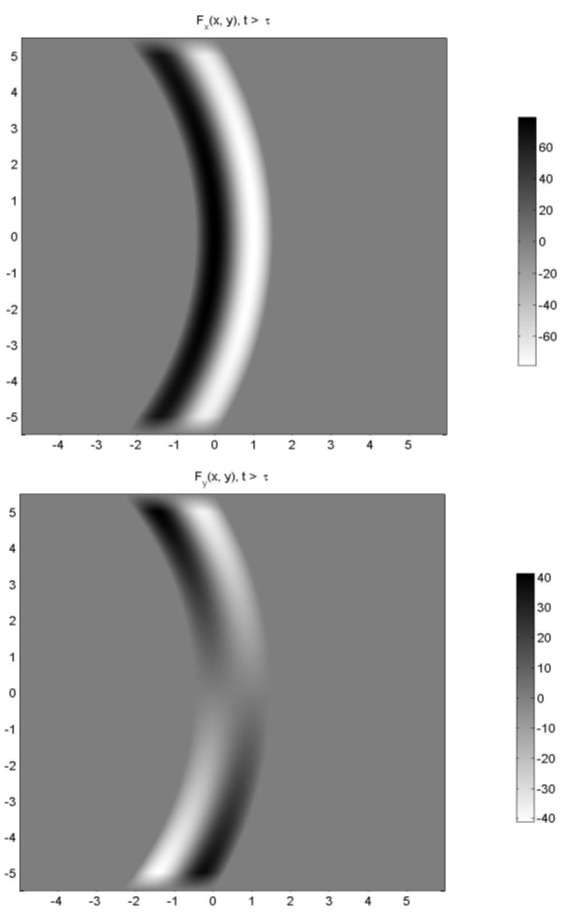
Граничные условия были заданы свободными на всех границах области, кроме левой, через которую неоднородный сверхзвуковой поток газа попадает внутрь нее. Для уменьшения влияния верхней и нижней границ поле потенциальной ямы модифицировалось в буферных зонах шириной 0,5 пк вдоль каждой из границ так, чтобы амплитуда потенциала линейно убывала до 0 на самих границах. Распределение сил, создаваемое ямой после такой модификации, показано на рисунке 2.

Характеристикой, определяющей степень неоднородности вещества МЗС, является фактор объемного заполнения f среды облаками. Он определяется как отношение объема, занятого облаками к объему рассматриваемого участка МЗС f = V_c/V. Обычно он, в зависимости от области галактики, принимает значения от 0,001 до 0,1. В данной работе на левой границе расчетной области значения плотности газа генерировались так, чтобы результирующий фактор заполнения был равен 0,05. Кроме того, на значения концентрации псевдослучайным образом накладывались малые возмущения в 10% от фонового значения, для фрагментов облаков концентрация принимала значения n = 120±12 (в безразмерных единицах), а для межоблачных – n = 1±0,1. При этом скорость и давления вещества согласно (14) одинаковы как в облаках, так и в межоблачном газе: p = 8, v_0x = 3-8.

В качестве начального условия было принято равномерное распределение газа по расчетной области со следующими значениями величин: n = 1, p = 8, v_0x = 3-8, причем скорость течения выбиралась такой же, как и на левой границе. Для сравнения также были проведены расчеты в адиабатическом приближении и без самогравитации при прочих равных условиях.

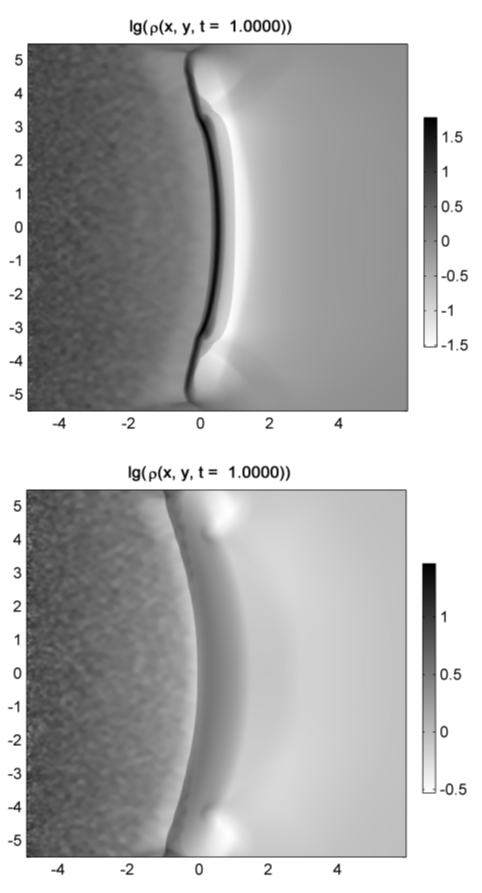
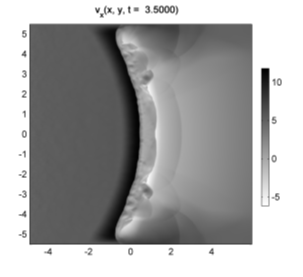
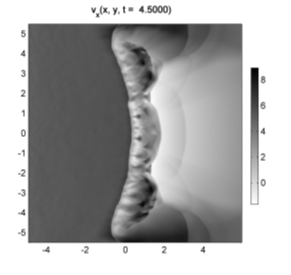
Результаты вычислений показаны на рисунках 3-8. При формировании потенциальной ямы в ее правой (задней по отношению к направлению движения газа) части в первоначально однородном течении появляется ударная волна, которая затем перемещается против течения ближе к средней линии ямы. Это согласуется с результатами более ранних работ, в которых рассматривалось только адиабатическое течение. Однако учет неадиабатических процессов и самогравитации существенно изменяет характер движения газа за фронтом ударной волны. Во-первых, в этой области течения плотность газа существенно больше (в 10 раз), чем в адиабатическом случае. Во-вторых, это мощное уплотнение дает дополнительный вклад в гравитационное поле потенциальной ямы, под действием которого в газе возникает противоток и формируется еще одна ударная волна (см. рисунок 3) также на задней кромке ямы. Затем вторичная ударная волна покидает потенциальную яму.

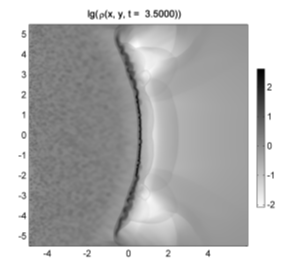
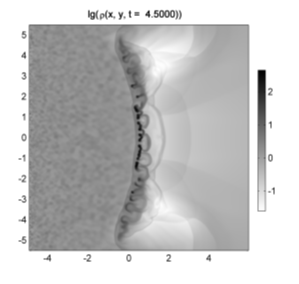
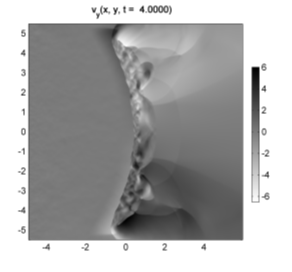
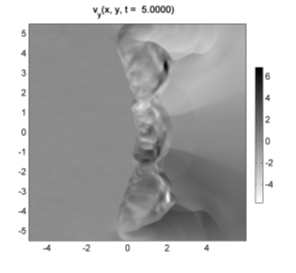
В дальнейшем характер течения становится полностью отличным от адиабатической модели. На временах t = 3,3-4 в зафронтовом течении газ фрагментирует на отдельные сгустки с концентрацией ~100 и внутренней энергией ~1. Это свидетельствует о том, что в первичном уплотнении произошел фазовый переход и начала развиваться тепловая неустойчивость. Ее развитию также способствуют флуктуации параметров в натекающем потоке газа. Необходимо отметить, что некоторый вклад в неустойчивость течения дают верхняя и нижняя границы. Однако, как это видно из рисунка 8, в окрестности этих границ газ попадает в расчетную область уже за фронтом волны и вообще за областью, где формируются уплотнения.

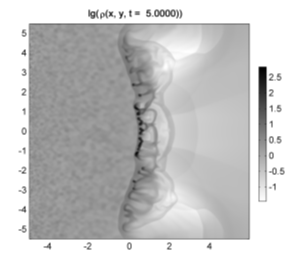
На временах t = 4-5,5 в течении газа образуются два режима натекания. В центральной области при |y| < 1,5 вновь возникает зона противотока. При этом плотности газа здесь достигают значений ~300-400. Структура этого течения наиболее напоминает аккреционный фронт, который является одной из альтернатив ГУВ при наличии самогравитации. Он неограниченно аккумулирует в себя вещество, при этом натекание на него происходит со всех сторон. В нашем случае развитие фрагментации разрушает его целостность уже на стадии формирования, поэтому вместо одного мощного уплотнения образуется несколько мелких размером около 0,2-0,4 кпк.

В областях |y| > 1.5 ударная волна смещается ближе к задней кромке ямы. Газ за ее фронтом фрагментирует на несколько менее плотных (плотность ~150) конденсаций. С ними также связаны протяженные (до 1,5 кпк) шлейфы вещества, развитие которых в центральной области из-за противоточного течения не так заметно выражено.

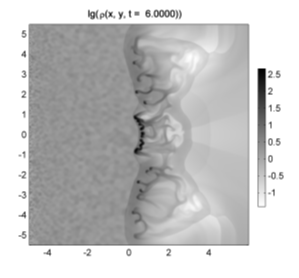
Поведение УВ и зафронтового течения в целом не стационарно. Во многом это связано с общим турбулентным характером движения газа после прохождения через яму. Ко временам t = 5,5-6 фронт УВ четко разделяется на центральную и боковые зоны и смещается по направлению течения. Еще позднее при t> 7 ударная волна и сформировавшаяся облачная структура окончательно отрываются от потенциальной ямы. Эффект нестационарности и отрыва обнаруживается во всем диапазоне v_0x = 3-8 исследованных скоростей натекания.

Заключение

Учет самогравитации и тепловых процессов существенным образом изменяет характер течения газа в сравнении с чисто адиабатической моделью. Во-первых, ударная волна становится инициирующим механизмом для развития тепловой и гравитационной неустойчивостей, что приводит к фрагментации течения на отдельные облака. Во-вторых, фронт ударной волны не сплошной, в течении одновременно могут сосуществовать как области с ударной волной, так и области с аккреционным фронтом. Это может свидетельствовать в пользу того, что в реальных условиях ГУВ на самом деле представляют собой систему нескольких ударных волн.

Библиографический список

1. Wada K., Koda J. Multi-Phase Gas Dynamics in aWeak Barred Potential.// PASJ – 2001. – V.53. – P.1163-1170.
2. Wada K., Norman C. A. The global structure and evolution of a self-gravitating multiphase interstellar medium in a galactic disk. // Astrophys. J.- 1999. – V. 516. – P. 13-16.
3. Harten A. High resolution schemes for hyperbolic conservation laws. // J. Comput. Phys. – 1983. – V. 49. – P. 357-393.
4. Harten A. On the symmetric form of systems of conservation laws with entropy // J. Comput. Phys. – 1983. – V. 49. – P. 151-164.
5. Toth G., Odstrcil D. Comparison of some flux corrected transport and total variation diminishing numerical schemes for hydrodynamic and magnetohydrodynamic problems. // J. Comput. Phys. – 1996. – V. 128. – P. 82-100.
6. Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.
7. Press W., Teukolsky S., Vetterling W., Flannery B. Numerical Recipes in C, Second Edition. Cambridge University Press, 1992.

---

Количество просмотров публикации: Please wait

Все статьи автора «Барышников Андрей Николаевич»