Введение.
Работа посвящена вопросам оценивания рисков интегрированных проектов (ИП) на основе потоковых моделей бизнес-процессов и является продолжением исследований начатых и опубликованных в [1]-[3]. Здесь приведены модели бизнес-процессов, которые фактически являются своеобразной детализацией частных проектов ИП и самого ИП – в том числе.
Потоковые модели бизнес-процессов.
Потоковые модели бизнес-процессов [4] – удобный аппарат для анализа ИП на риски, проведения факторного анализа и анализа на чувствительность ИП, для выработки управлений в рамках ИП и для решения многих других задач (см. подробнее о методах анализа рисков в работах [5]-[25]).
Введем в рассмотрение модели каждого из проектов, входящих в ИП, в виде потоковых моделей бизнес-процессов (см. [25]-[35]). Для основных (базовых) проектов ИП введём в рассмотрение ![]() соответствующих им базовых бизнес-процессов (БП)
соответствующих им базовых бизнес-процессов (БП) ![]() в виде множества:
в виде множества:
![]() . (1)
. (1)
Произвольный бизнес-процесс ![]() ,
, ![]() , зададим в виде кортежа:
, зададим в виде кортежа:
![]() ,
,
где
![]() – поток работ для
– поток работ для ![]()
![]()
![]() – поток ресурсов для процесса
– поток ресурсов для процесса ![]()
![]()
![]()
![]() – входной (затратный) финансовый поток
– входной (затратный) финансовый поток ![]()
![]() =
=![]() – выходной (доходный) финансовый поток
– выходной (доходный) финансовый поток ![]()
![]() – момент инициализации процесса
– момент инициализации процесса ![]()
![]() – момент инициализации процессом
– момент инициализации процессом ![]() следующего процесса;
следующего процесса;
![]() – момент запуска
– момент запуска ![]()
![]() – продолжительность
– продолжительность ![]()
![]() – поток выпущенных (произведенных) продуктов (товаров, изделий, услуг и т.д.) процессом
– поток выпущенных (произведенных) продуктов (товаров, изделий, услуг и т.д.) процессом ![]() .
.
Отметим, что каждый из процессов ![]() может быть определен также и некоторыми другими характеристиками. Например, это могут быть функции интенсивности расходования ресурсов
может быть определен также и некоторыми другими характеристиками. Например, это могут быть функции интенсивности расходования ресурсов ![]() в единицу времени, стоимости работ и другие. Все множество факторов (характеристик, переменных)
в единицу времени, стоимости работ и другие. Все множество факторов (характеристик, переменных) ![]() можно разбить на внутренние относительно фиксированного БП (например,
можно разбить на внутренние относительно фиксированного БП (например, ![]() и, возможно, некоторые другие) и внешние относительно этого БП (например,
и, возможно, некоторые другие) и внешние относительно этого БП (например, ![]() , и другие). Условно эту особенность процессов можно изобразить следующим образом (см. Рис. 1).
, и другие). Условно эту особенность процессов можно изобразить следующим образом (см. Рис. 1).
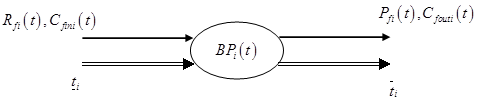
Рисунок 1. Внутренние и внешние факторы БП ![]()
Следует заметить, что в общем случае факторы ![]() и
и ![]() могут быть также векторными и их значения могут содержать сведения о состоянии работ, о состоянии выходных финансовых потоков и некоторые другие. Конечно, в общем случае времена
могут быть также векторными и их значения могут содержать сведения о состоянии работ, о состоянии выходных финансовых потоков и некоторые другие. Конечно, в общем случае времена ![]() и
и ![]() не совпадают, также как и времена
не совпадают, также как и времена ![]() и
и ![]()
Заметим, что во множество процессов ![]() могут быть включены как собственные бизнес-процессы из множества
могут быть включены как собственные бизнес-процессы из множества ![]() (соответствуют собственным проектам в ИП), так и бизнес-процессы из множествапроцессов среды
(соответствуют собственным проектам в ИП), так и бизнес-процессы из множествапроцессов среды ![]() (внешнего окружения, внешние, соответствуют внешним проектам), т.е. в общем случае множество
(внешнего окружения, внешние, соответствуют внешним проектам), т.е. в общем случае множество ![]() может быть представлено в виде объединения
может быть представлено в виде объединения ![]() , причем,
, причем, ![]() . В этом случае
. В этом случае ![]() – это структурированные процессы из
– это структурированные процессы из ![]() , а
, а ![]() – это множество структур
– это множество структур ![]() , в которых отсутствуют (исключены) элементы из
, в которых отсутствуют (исключены) элементы из ![]() . Операторы преобразования бизнес-процессов
. Операторы преобразования бизнес-процессов ![]() ,
, ![]() ,
, ![]() (множество операторов –
(множество операторов – ![]() ) в паре с исходным множеством бизнес-процессов
) в паре с исходным множеством бизнес-процессов ![]() порождают конструктор ИП, т.е.
порождают конструктор ИП, т.е. ![]() . Таким образом, операторы из
. Таким образом, операторы из ![]() позволяют получать (генерировать) множество моделей из бизнес-процессов более сложной природы, структурированные (имеющие определенную структуру, объединенные в определенную структуру) и согласованные внутри структуры по факторам (характеристикам, параметрам бизнес-процессов). Результатом применения конструктора
позволяют получать (генерировать) множество моделей из бизнес-процессов более сложной природы, структурированные (имеющие определенную структуру, объединенные в определенную структуру) и согласованные внутри структуры по факторам (характеристикам, параметрам бизнес-процессов). Результатом применения конструктора ![]() к процессам из
к процессам из ![]() служит процесс
служит процесс ![]() (модель ИП в виде бизнес-процесса).
(модель ИП в виде бизнес-процесса).
Оценивание эффективности ИП на основе потоковых моделей бизнес-процессов.
Оценивание эффективности ИП с использованием потоковой модели бизнес-процессов предполагает введение в рассмотрение показателей. Они характеризуют ИП и принадлежит к классам критериев эффективности. В качестве критерия эффективности может выступать прибыль, а в качестве показателей – общая или чистая прибыль, дисконтированное или компаундированное значение прибыли и пр. Для показателей соответствующих критериев эффективности введем обозначение: ![]() .
.
Значения показателей ИП будем оценивать показателями для модели ИП в виде совокупности взаимосвязанных и соответствующих этому проекту бизнес-процессов. Для этого предварительно приводим потоки каждого бизнес-процесса ![]() , к виду, удобному для оценивания того или иного показателя. Так, для примера, оценивание показателей
, к виду, удобному для оценивания того или иного показателя. Так, для примера, оценивание показателей ![]() ,
, ![]() ,
, ![]() предполагает пересчет потоков процесса
предполагает пересчет потоков процесса ![]() в соответствии со следующей схемой:
в соответствии со следующей схемой:
- потоки ![]() ,
, ![]() и
и ![]() необходимо пересчитать в обобщенный поток
необходимо пересчитать в обобщенный поток ![]()
![]() ,
, ![]() ;
;
- потоки ![]() ,
, ![]() следует пересчитать в обобщенный поток
следует пересчитать в обобщенный поток ![]()
![]() ,
, ![]()
Без умаления общности можно считать, что ![]() =
=![]() =
=![]() и
и ![]() =
=![]() =
=![]() . Это означает, что в модели бизнес-процесса
. Это означает, что в модели бизнес-процесса ![]() в качестве входного и выходного потоков были представлены обобщенные потоки. Если это не так, то необходимо выполнить следующие очевидные манипуляции над потоками бизнес-процесса.
в качестве входного и выходного потоков были представлены обобщенные потоки. Если это не так, то необходимо выполнить следующие очевидные манипуляции над потоками бизнес-процесса.
Используемые в расчетах для показателей параметры (такие, как ставки компаундирования, дисконтирования, заемного процента и т.д.) должны быть в паре с соответствующими им потоками и выглядеть, например, так: ![]() ,
, ![]() , где
, где![]() – ставка компаундирования,
– ставка компаундирования, ![]() – ставка дисконтирования для
– ставка дисконтирования для ![]() ,
, ![]() – стоимость
– стоимость ![]() . Количество параметров, приписываемых тем или иным потокам, зависит от реальной задачи, от используемых для оценивания эффективности бизнес-процессов критериев эффективности и соответствующих им показателей. В качестве параметров могут выступать также стоимость работ, материалов, услуг, оборудования, энергоресурсов и т.д. Для выходных потоков параметрами могут быть цены на произведенную продукцию, ставки внешнего использования свободных финансовых средств, стоимость оказываемых услуг для сторонних организаций и многое другое. Если для параметров использовать обозначение
. Количество параметров, приписываемых тем или иным потокам, зависит от реальной задачи, от используемых для оценивания эффективности бизнес-процессов критериев эффективности и соответствующих им показателей. В качестве параметров могут выступать также стоимость работ, материалов, услуг, оборудования, энергоресурсов и т.д. Для выходных потоков параметрами могут быть цены на произведенную продукцию, ставки внешнего использования свободных финансовых средств, стоимость оказываемых услуг для сторонних организаций и многое другое. Если для параметров использовать обозначение ![]() с индексами
с индексами ![]() ,
, ![]() , то параметризованные потоки будут иметь вид:
, то параметризованные потоки будут иметь вид: ![]() ,
, ![]() .
.
Преобразование потоков бизнес-процесса в параметризованную форму формально имеет вид:
![]()
(для одного показателя ![]() ) и
) и
![]()
(для множества показателей ![]() ),
), ![]() .
.
Хорошо известно, что классические показатели эффективности БП и ИП (такие, как ![]() ,
, ![]() ,
, ![]() ,
, ![]() и многие другие) имеют недостатки, которые делают их малопригодными для практического использования. Так, для показателя
и многие другие) имеют недостатки, которые делают их малопригодными для практического использования. Так, для показателя ![]() характерны следующие моменты: выбор ставки дисконтирования для него является достаточно субъективным, он не имеет ясного экономического смысла, не учитывает доходы второго уровня и т.д. Показатели
характерны следующие моменты: выбор ставки дисконтирования для него является достаточно субъективным, он не имеет ясного экономического смысла, не учитывает доходы второго уровня и т.д. Показатели ![]() ,
, ![]() ,
, ![]() и некоторые другие являются производными от
и некоторые другие являются производными от ![]() , поэтому они переняли от
, поэтому они переняли от ![]() (так сказать, от «прародителя») недостатки характерные для них. Показатель
(так сказать, от «прародителя») недостатки характерные для них. Показатель ![]() не оценивает значение доходности бизнес-процессов. Подробно с проблемами классических показателей и подходами к их устранению можно ознакомиться в работах [33]-[35]. Для практического использования мы рекомендуем модификации показателя
не оценивает значение доходности бизнес-процессов. Подробно с проблемами классических показателей и подходами к их устранению можно ознакомиться в работах [33]-[35]. Для практического использования мы рекомендуем модификации показателя ![]() и производных от них (см. [1]-[3]). В этом случае могут быть применены различные ставки: ставки банка по заемным средствам, по депозитам, внешнего использования и пр. Тогда, показатель
и производных от них (см. [1]-[3]). В этом случае могут быть применены различные ставки: ставки банка по заемным средствам, по депозитам, внешнего использования и пр. Тогда, показатель ![]() , вычисленный на основе модификаций критерия
, вычисленный на основе модификаций критерия![]() (например, такой как
(например, такой как ![]() ), будет оценивать фактическую доходность бизнес-процессов и ИП.
), будет оценивать фактическую доходность бизнес-процессов и ИП.
Риски интегрированных проектов и их оценивание через риски соответствующих бизнес-процессов.
Потоковые модели бизнес-процессов – это удобное представление ИП для решения задач оценивания и оптимизации рисков. Риски ИП и соответствующих им БП ![]() обусловлены неопределенностями в знании характеристик БП
обусловлены неопределенностями в знании характеристик БП ![]() и их параметров
и их параметров ![]() . Будем обозначать БП с неопределенностями как
. Будем обозначать БП с неопределенностями как ![]() , а для их параметров –
, а для их параметров –![]() . Причем, разложения
. Причем, разложения ![]() , соответствуют внутренним и внешним БП (проектам и ИП) и их параметрам. Очевидно, такая неопределенность в знании характеристик ИП (и соответствующих им БП) приводит к тому, что вместо вектора показателей
, соответствуют внутренним и внешним БП (проектам и ИП) и их параметрам. Очевидно, такая неопределенность в знании характеристик ИП (и соответствующих им БП) приводит к тому, что вместо вектора показателей ![]() (или
(или ![]() ) практически придется иметь дело с вектором
) практически придется иметь дело с вектором ![]() (или с векторами
(или с векторами ![]() ). Величина, характеризующая отклонение вектора
). Величина, характеризующая отклонение вектора ![]() от вектора
от вектора ![]() и будет оценкой риска ИП. Следует заметить, что в общем случае вектор показателей
и будет оценкой риска ИП. Следует заметить, что в общем случае вектор показателей ![]() может зависеть от времени (случай динамических показателей эффективности ИП), т.е.
может зависеть от времени (случай динамических показателей эффективности ИП), т.е. ![]() , а это означает, что и соответствующие им (и показателям
, а это означает, что и соответствующие им (и показателям ![]() ) риски будут тоже зависеть от времени (случай динамических рисков). Очевидно, что процедура оценивания рисков (в динамике – оценивание вектора рисков
) риски будут тоже зависеть от времени (случай динамических рисков). Очевидно, что процедура оценивания рисков (в динамике – оценивание вектора рисков ![]() , вектора размерности
, вектора размерности ![]() ) может быть условно представлена отображением:
) может быть условно представлена отображением:
![]() ,
,
где ![]() – оператор оценивания рисков. Схема перехода от пары
– оператор оценивания рисков. Схема перехода от пары ![]() к вектору рисков
к вектору рисков ![]() , может быть изображена таким образом:
, может быть изображена таким образом:
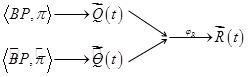
Заметим, что вектор ![]() включает в себя как внутренние, так и внешние риски (
включает в себя как внутренние, так и внешние риски (![]() и
и ![]() ). Точнее, как риски, обусловленные внутренними характеристиками бизнес-процессов (
). Точнее, как риски, обусловленные внутренними характеристиками бизнес-процессов (![]() и
и ![]() ), так и внешними характеристиками (
), так и внешними характеристиками (![]() и
и ![]() ).
).
Приведем основные определения рисков и расчетные формулы для их оценивания.
Определение 11.1.
Риск ![]() называется условно-внутренним, если он получен для пары
называется условно-внутренним, если он получен для пары ![]() при фиксированных значениях другой пары –
при фиксированных значениях другой пары – ![]() .
.
Определение 11.2.
Риск ![]() называется условно-внешним, если он получен для
называется условно-внешним, если он получен для ![]() при фиксированных значениях
при фиксированных значениях ![]() .
.
Следует отметить, что в общем случае ![]() и
и ![]() . Сказанное может быть проиллюстрировано на рисунке (см. Рис. 2).
. Сказанное может быть проиллюстрировано на рисунке (см. Рис. 2).
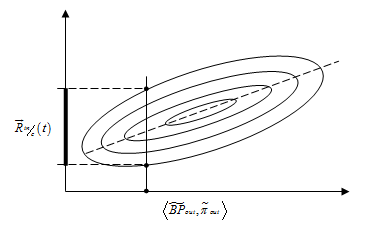
Рисунок 2. Иллюстрация к определению условного риска
Проведенные исследования показали, что для задач управления проектами (частых случаев задач управления бизнес-процессами) условие аддитивности рисков не выполняется. Как следствие этого, можно сделать следующие выводы:
- оценивание рисков величинами дисперсий неоправданно, т.к. дисперсия является мерой неопределенности, а не риска;
- оценивание рисков на основе квантильных подходов (например, на основе ![]() -подхода к оцениванию рисков) является более оправданным, чем оценивание с помощью дисперсий, однако необходимо учитывать, что эффективность бизнес-процессов, как правило, оценивается векторным показателем эффективности
-подхода к оцениванию рисков) является более оправданным, чем оценивание с помощью дисперсий, однако необходимо учитывать, что эффективность бизнес-процессов, как правило, оценивается векторным показателем эффективности ![]() и, как следствие, риски, в общем случае, являются зависимыми;
и, как следствие, риски, в общем случае, являются зависимыми;
- как следует из утверждения выше, оценивание рисков ![]() необходимо проводить с учетом их зависимости друг от друга; причем, эта зависимость носит как детерминированный, так и случайный характер;
необходимо проводить с учетом их зависимости друг от друга; причем, эта зависимость носит как детерминированный, так и случайный характер;
- в общем случае независимое оценивание рисков ![]() и
и ![]() представляется невозможным, и при этом необходимо учитывать справедливость неравенств
представляется невозможным, и при этом необходимо учитывать справедливость неравенств ![]() и
и ![]() .
.
Существует достаточно большое разнообразие операторов оценивания рисков ![]() . Так, в работе [36] (см. стр. 114-127) приведены пятнадцать видов этих операторов. Заметим, что количество их может быть существенно увеличено и при этом каждый новый вид такого оператора будет определяться желаниями (потребностями, необходимостью) аналитиков и практиков управления бизнес-процессами (и соответствующими им проектами) оценить различия (отклонения) между номинальными значениями показателей
. Так, в работе [36] (см. стр. 114-127) приведены пятнадцать видов этих операторов. Заметим, что количество их может быть существенно увеличено и при этом каждый новый вид такого оператора будет определяться желаниями (потребностями, необходимостью) аналитиков и практиков управления бизнес-процессами (и соответствующими им проектами) оценить различия (отклонения) между номинальными значениями показателей ![]() и их возмущенными значениями
и их возмущенными значениями ![]() .
.
В каждом таком конкретном случае введения метрики для измерения рисков бизнес-процессов будет, тем самым, введена метрика в пространстве значений показателей эффективности бизнес-процессов, которая и будет определять вид оператора ![]() :
:
![]() .
.
Так, например, выражение для риска вида
![]() ,
,
где ![]() – вектор номинальных значений показателей,
– вектор номинальных значений показателей, ![]() – функция плотности вероятностей
– функция плотности вероятностей ![]() -мерной случайной величины
-мерной случайной величины
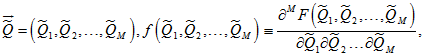
![]() – функция совместного распределения вероятностей вектора
– функция совместного распределения вероятностей вектора ![]() , задает риск для бизнес-процесса
, задает риск для бизнес-процесса ![]() . Смысл этого риска состоит в том, что он оценивает вероятность того, что значения возмущенных показателей будут меньше своих номинальных значений. Конечно, в этом случае предполагается, что уменьшение значений показателей
. Смысл этого риска состоит в том, что он оценивает вероятность того, что значения возмущенных показателей будут меньше своих номинальных значений. Конечно, в этом случае предполагается, что уменьшение значений показателей ![]() относительно номинальных значений приводит к потерям, а увеличение – к таковым не приводит.
относительно номинальных значений приводит к потерям, а увеличение – к таковым не приводит.
Приведем еще примеры операторов ![]() для оценивания рисков бизнес-процессов.
для оценивания рисков бизнес-процессов.
Так, риск
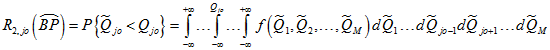 ,
,
оценивает вероятность того, что только по ![]() -му показателю возмущенное значение этого показателя будет меньше номинального значения.
-му показателю возмущенное значение этого показателя будет меньше номинального значения.
Приведем иллюстрацию для риска ![]() (см. Рис. 3).
(см. Рис. 3).
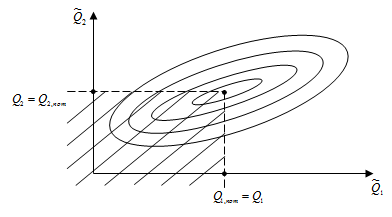
Рисунок 3. Иллюстрация к оцениванию риска ![]()
На Рис. 3 в координатных осях ![]() и
и ![]() показаны линии равного уровня плотности вероятностей
показаны линии равного уровня плотности вероятностей ![]() , а заштрихованная область – область, интегрирование по которой и позволяет найти оценку риска
, а заштрихованная область – область, интегрирование по которой и позволяет найти оценку риска ![]() .
.
Следующий оператор ![]() , оценивающий риск как наибольшие абсолютные потери, порождает класс рисков вида:
, оценивающий риск как наибольшие абсолютные потери, порождает класс рисков вида:
![]() ,
,
где ![]() – наименьшее значение возмущенного показателя
– наименьшее значение возмущенного показателя ![]() .
.
На Рис. 4 приведена иллюстрация для оценок этого вида риска для случая двух показателей ![]() и
и ![]() .
.
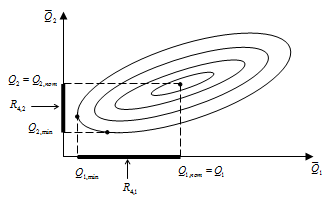
Рисунок 4. Оценивание рисков через наибольшие абсолютные потери
Рассмотрим случай оценивания рисков через ![]() , т.е. для случая, когда риски оцениваются наибольшими возможными абсолютными потерями. В этом случае пары
, т.е. для случая, когда риски оцениваются наибольшими возможными абсолютными потерями. В этом случае пары ![]() , можно получить несколькими способами. Один из таких способов показан на Рис. 5.
, можно получить несколькими способами. Один из таких способов показан на Рис. 5.
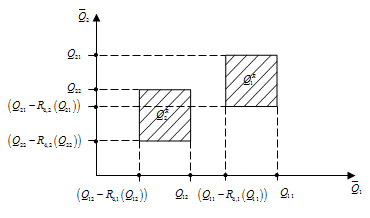
Рисунок 5. Возможные соотношения пар ![]()
Следует заметить, что оценки рисков можно классифицировать как по их экономико-математическому смыслу (вероятностные риски возможных потерь; наибольшие абсолютные потери или риски, связанные с наибольшими финансовыми потерями и т.д.), так и по тому, оценивают ли они эти характеристики для каждого из показателей в отдельности (индивидуальные риски) или для всей совокупности показателей в целом (общие риски). Очевидно, индивидуальными рисками можно воспользоваться, если объединить их в пары с самими показателями, например, вида ![]() ,
, ![]() – номер (индекс) вида риска или
– номер (индекс) вида риска или ![]()
![]() , если каждому из показателей сопоставить множество оценок рисков
, если каждому из показателей сопоставить множество оценок рисков ![]() , ему соответствующих. Такие пары порождают характеристики бизнес-процессов вида
, ему соответствующих. Такие пары порождают характеристики бизнес-процессов вида ![]() , где
, где ![]() . Если множество видов рисков зафиксировано, то интерес представляет ответ на вопрос: как выбрать (найти) лучший бизнес-процесс (соответствующий ИП), опираясь на вектор
. Если множество видов рисков зафиксировано, то интерес представляет ответ на вопрос: как выбрать (найти) лучший бизнес-процесс (соответствующий ИП), опираясь на вектор ![]() ? Другими словами, требуется определить отношение предпочтения бизнес-процессов с использованием векторов
? Другими словами, требуется определить отношение предпочтения бизнес-процессов с использованием векторов ![]() , т.е. дать определение отношению
, т.е. дать определение отношению
![]()
с учетом рисковых составляющих ![]()
![]() .
.
Будем предполагать, что для всех частных показателей ![]() ,
, ![]() вектора
вектора ![]() выполняется условие
выполняется условие ![]() или
или ![]() . Здесь
. Здесь ![]() и
и ![]() – значения
– значения ![]() -ых показателей для двух бизнес-процессов
-ых показателей для двух бизнес-процессов ![]() и
и ![]() .
.
Очевидно, что в общем случае предпочтение ![]() формализовать значительно сложнее, чем предпочтение
формализовать значительно сложнее, чем предпочтение ![]() , поскольку наряду с самими номинальными значениями показателей
, поскольку наряду с самими номинальными значениями показателей ![]() необходимо учитывать и соответствующие им риски.
необходимо учитывать и соответствующие им риски.
Одним из способов формализации отношения предпочтения в этих случаях может служить использование функций полезности ![]() , например, следующего вида:
, например, следующего вида:
.gif)
где функции ![]() и
и ![]() определяют отношение аналитика бизнес-процессов (и соответствующих ИП) к принадлежности (или непринадлежности) вектора
определяют отношение аналитика бизнес-процессов (и соответствующих ИП) к принадлежности (или непринадлежности) вектора ![]() области
области ![]() желаемых значений показателей бизнес-процесса. В этом случае рекомендуется воспользоваться (в качестве показателя
желаемых значений показателей бизнес-процесса. В этом случае рекомендуется воспользоваться (в качестве показателя ![]() ) показателем общей полезности, который можно оценить, например, следующим образом:
) показателем общей полезности, который можно оценить, например, следующим образом:
![]() ,
,
и тогда отношение предпочтения для бизнес-процессов с использованием функции полезности можно представить так: ![]() .
.
Вид функций ![]() и преобразований показателей
и преобразований показателей ![]() можно выбирать в зависимости от субъективных (или объективных) предпочтений и, таким образом, вводить в рассмотрение для последующего оценивания и сравнительного анализа всё новые метрики, которые будут служить основой (базой) для отношений
можно выбирать в зависимости от субъективных (или объективных) предпочтений и, таким образом, вводить в рассмотрение для последующего оценивания и сравнительного анализа всё новые метрики, которые будут служить основой (базой) для отношений ![]() .
.
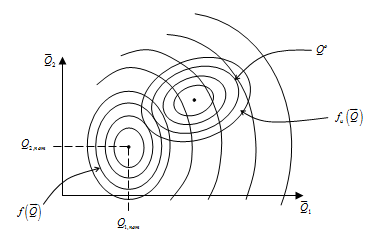
На Рис. 6 проиллюстрирован вид функций ![]() и
и ![]() (линиями равного уровня), показана точка номинальных значений показателей
(линиями равного уровня), показана точка номинальных значений показателей ![]() и область
и область ![]() желаемых значений показателей
желаемых значений показателей ![]() .
.
.gif)
Библиографический список
- Наумов А.А., Наумова А.А. Оценивание эффективности интегрированных проектов на основе метода детализации финансовых потоков// Современные научные исследования и инновации. 2015. № 7 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/07/56645 (дата обращения: 31.07.2015).
- Наумов А.А., Наумова А.А. К оцениванию эффективности интегрированных проектов// Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/56856 (дата обращения: 25.08.2015).
- Наумов А.А., Наумова А.А. Новый подход к оцениванию доходности и оптимизация интегрированных проектов // Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/57215 (дата обращения: 31.08.2015).
- Наумов А.А. Методы анализа и синтеза инвестиционных проектов. Эффективность, риски, управление. LAP LAMBERT Academic Publishing, 2013.
- Балабанов И.Т. Риск-менеджмент. М., 1996.
- Балдин К.В., Воробьев С.Н. Риск-менеджмент: Учебное пособие. М., 2005.
- Гибсон Р. Формирование инвестиционного портфеля: управление финансовыми рисками. М., 2005.
- Гранатуров В.М. Экономический риск: сущность, методы измерения, пути снижения. М., 1999.
- Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых ситуаций в экономике и бизнесе. М., 1999.
- Иода Е.В., Иода Ю.В., Мешкова Л.Л., Болотина Е.Н. Управление предпринимательскими рисками. Тамбов, 2002.
- Качалов Р.М. Управление хозяйственным риском. М., 2002.
- Лапуста М.Г., Шаршукова Л.Г. Риски в предпринимательской деятельности. М., 1998.
- Первозванский А.А., Первозванская Т.Н. Финансовый рынок: расчет и риск. М., 1994.
- Хохлов Н.В. Управление риском. М., 1999.
- Чернов В.А. Анализ коммерческого риска. М., 1998.
- Шапкин А.С. Экономические и финансовые риски. Оценка, управление, портфель инвестиций. М., 2003.
- Balakrishnan N., Naumov A., Morgunov D. Methods of Estimation of Risks and Analysis of Business Processes// Methods and Applications of Statistics in Business, Finance, and Management Science (N. Balakrishnan, Editor). Wiley. 2010. pp. 245-272.
- Наумов А.А., Федоров А.А. Риски в задачах синтеза эффективного портфеля проектов// Вестник Красноярского государственного университета: физико-математические науки. 2006. №4. С. 117-125.
- Наумов А.А., Шубин Д.А. К оцениванию рисков бизнес-процессов// Вестник НГУ. Серия: Социально-экономические науки. 2008. Том 8. Вып. 4. С. 56-67.
- Наумов А.А., Федоров А.А. Меры риска портфеля проектов// Всероссийская ФАМ’2006 конференция: Тр. V Всерос. конф. по финансово-актуарной математике и смежным вопросам. Ч. 2. Красноярск. 2006. С. 248-254.
- Наумов А.А., Федоров А.А. Риски в задачах синтеза эффективного портфеля проектов// Вестник Красноярского государственного университета: физико-математические науки. 2006. №4. С. 117-125.
- Наумов А.А., Федоров А.А. Подходы к оцениванию риска портфеля проектов// Информационные технологии моделирования и управления. 2006. Вып. 3 (28). С. 306- 315.
- Наумов А.А. Анализ рисков и обратные задачи для исследования инвестиционных проектов// Theoretical & Applied Science, Materials of the ISPC «Applied scientific research», 30.11.2013, Belgrade, Serbia. 2013. №11(7). Vol. 1. С. 99-101.
- Наумов А.А. К задаче оценивания эффективности и рисков инновационных кластеров// Управление риском. 2011. № 4. С. 61-64.
- Наумов А.А., Жанатауов С.У. Использование размытых множеств при оценивании рисков инвестиционных проектов// ISJ Theoretical&Applied Science, Materials of the ISPC «Computer technologies in science», 30.04.2014, Valencia, Venezuela. 2014. № 4 (12). С. 178-181.
- Наумов А.А., Шубин Д.А. К задаче построения алгебры инвестиционных проектов// Сборник научных трудов НГТУ. 2006. № 3(45). С. 109-114.
- Наумов А.А., Бах С.А. Бизнес-процессы. Синтез, анализ, моделирование и оптимизация. Новосибирск, 2007.
- Наумов А.А., Максимов М.А. Управление экономическими системами. Процессный подход. Новосибирск, 2008.
- Наумов А.А. Математические модели и методы управления экономическими системами на основе процессного подхода// Доклады АН ВШ РФ. 2010. № 1(14). С. 26-35.
- Наумов А.А., Клавсуц И.Л., Лямзин О.Л. Инновации. Теория, модели, методы управления. Новосибирск, 2010.
- Наумов А.А. Управление бизнес-процессами. Синтез, анализ, моделирование и оптимизация. LAP LAMBERT Academic Publishing GmbH & Co. KG, 2011.
- Наумов А.А. К задаче оценивания эффективности и рисков инновационных кластеров// Управление риском. 2011. № 4. С. 61-64.
- Наумов А. А. Теоретические и прикладные вопросы моделирования бизнес-процессов. Модели, алгоритмы, программы: Монография. LAP LAMBERT Academic Publishing, 2012.
- Наумов А.А. Управление портфельными инвестициями. Эффективность, риски, оптимизация. LAP LAMBERT Academic Publishing, Saarbrucken, 2014.
- Наумов А.А. Интегрированные проекты. Анализ, синтез, управление. LAP LAMBERT Academic Publishing, Saarbrucken, 2015.
- Наумов А.А., А.А. Федоров Портфели инвестиционных проектов. Синтез, анализ и оптимизация. Новосибирск, 2006.
- Список трудов. [Электронный ресурс]. URL: https://sites.google.com/site/anatolynaumov2011/home/spisok-trudov-list-of-papers (Дата обращения 17.12.15).
