Студентами ПГУАС проводились геодезические работы на территории г. Пензы в районе улиц Ударная и Кулибина. На этой территории студенты сформировали семиугольный полигон (рис.1).

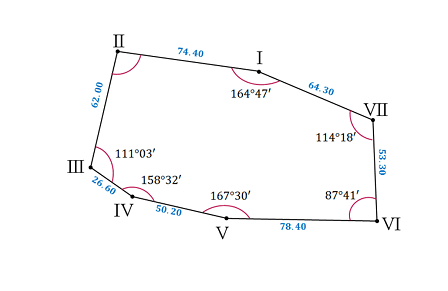
Рис.1. Схема теодолитного хода

Цель теодолитной съёмки сводилась к измерению длин сторон полигона и внутренних углов семиугольника. Итогом съёмки должны были стать вычисленные координаты семи угловых точек полигона. Были известны условные координаты первой точки полигона: X=600; Y=600. Ведомость вычисления координат точек теодолитного хода представлена в таблице 1.

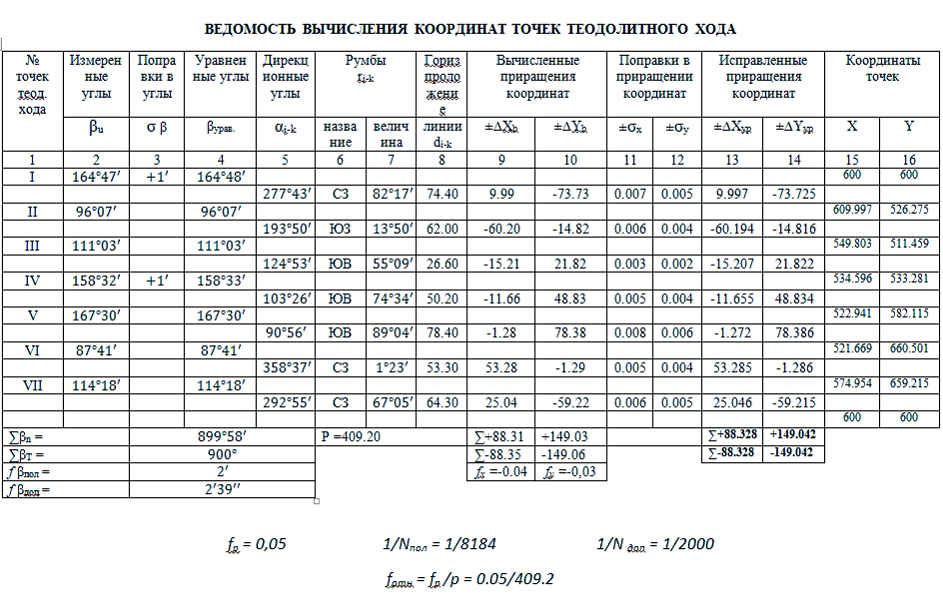
Работы, проводимые студентами условно разделим на несколько этапов:
Измерение внутренних углов и румбов
Измерение горизонтальных проложений
Расчёт приращений координат и координат точек
На первом этапе с помощью теодолита студенты измеряли внутренние углы в два приёма (при левом и правом круге теодолита). Затем с помощью среднего арифметического были вычислены окончательные значения углов (таблица 2).

№ точек теодолитного хода	Значение угла при круге право	Значение угла при круге лево	Полученные углы, βu
I
II
III
IV
V
VI
VII
Сумма
Теоретическая сумма

Исходя из этих данных, погрешность измерений равна: . Эта величина является угловой невязкой полигона. Данная невязка сравнивается с допустимой невязкой, которая определяется по формуле: , где n–число углов полигона:

Полученная невязка, разносится равномерно на все углы полигона, с обратным знаком. Невязка отрицательная, значит она вносится со знаком +. Для удобства (чтобы не было значений углов с секундами) по  было добавлено в первый и четвёртый значения углов (таблица 3).

Измеренные углы, βu	Поправки, σβ	Уравненные углы, βурав.

На втором этапе студенты с помощью рулетки измеряли длины сторон полигона (т.е. горизонтальные проложения). Измерения производились дважды: в прямом и обратном направлении. Затем с помощью среднего арифметического рассчитывались итоговые значения (таблица 4).

На третьем этапе теодолитной съёмки студенты рассчитывали приращения координат с помощью горизонтальных проложений и дирекционных углов α_i-k ( дирекционный угол – это угол, отсчитываемый от северного направления осевого меридиана до заданного направления) по формулам:


Сумма вычисленных приращений должна равняться 0. В результате расчётов были получены значения, представленные в таблице 5.

Обозначение линии	Дирекционные углы	Горизонтальное проложение линии	Вычисленные приращения координат
I-II	αi-k	di-k	±∆Xb±∆Yb
II-III		74.40	9.99-73.73
III-IV		62.00	-60.20-14.82
IV-V		26.60	-15.2121.82
V-VI		50.20	-11.6648.83
VI-VII		78.40	-1.2878.38
VII-I		53.30	53.28-1.29
I-II		64.30	25.04-59.22
			∑+88.31+149.03
			∑-88.35-149.06
			fx =-0.04fy =-0,03

В результате расчётов получились линейные невязки полигона по осям X и Y:


Абсолютная невязка полигона была определена по следующей формуле:

Для контроля правильности измерения полигона определим относительную невязку (относительной погрешностью называется отношение абсолютной погрешности к величине измеряемого объекта ):

где - абсолютная невязка полигона,
Р – периметр полигона (сумма горизонтальных проложений).
Для сравнения относительной невязки с допустимой, ее значение удобно преобразовать в простую дробь, числителем которой является 1. Для этого в дроби  числитель и знаменатель делим на . , т.е. полученная относительная невязка 1/N_пол =1/8184. Сравниваем полученную относительную невязку, с допустимой. Допустимая относительная невязка задается исходя из рельефа местности, так для сильно расчлененной, болотистой, кочковатой поверхности ее значение принимается = 1/1000, а для выровненной поверхности = 1/3000. В работе студентов значение 1/N =1/2000 принимается как для твердой поверхности со спокойным рельефом. Сравнивая относительные невязки 1/N_пол=1/8184<1/N_доп=1/2000 можно сделать вывод, что полученная невязка допустима, а значит измерения проведены правильно.
Для того чтобы избавиться от полученных невязок в значения приращений координат вносятся поправки σ_x и σ_y, которые рассчитываются по формулам : 


Суммы поправок равны невязкам и вносятся с обратным знаком.
Результаты расчётов представлены в таблице 6.
Результаты расчётов исправленных значений приращений координат

Обозначение линии	Вычисленные приращения координат	Поправки в приращении координат	Исправленные приращения координат
	±∆Xb	±∆Yb	±σx±σy±∆Xур±∆Yур
I-II	9.99	-73.73	0.0070.0059.997-73.725
II-III	-60.20	-14.82	0.0060.004-60.194-14.816
III-IV	-15.21	21.82	0.0030.002-15.20721.822
IV-V	-11.66	48.83	0.0050.004-11.65548.834
V-VI	-1.28	78.38	0.0080.006-1.27278.386
VI-VII	53.28	-1.29	0.0050.00453.285-1.286
VII-I	25.04	-59.22	0.0060.00525.046-59.215
	∑+88.31	+149.03	∑+88.328+149.042
	∑-88.35	-149.06	∑-88.328-149.042
	fx =-0.04	fy =-0,03

После этого определим координаты всех точек теодолитного хода, прибавляя к исходной координате значения приращений координат с учетом их знака.














Полученные значения координат первой точки совпадают с исходными, следовательно ведомость вычисления координат рассчитана правильно.

1. Быкова Ю.С., Гафарова Д.З., Снежкина О.В. Прикладная математика в задачах геодезии // Современные научные исследования и инновации. 2014. № 12 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/12/42283
2. В.Д. Большаков, Ю.М. Маркузе, Практикум по теории математической обработки геодезических измерений: учебное пособие для вузов. – 2-е изд., стереотипное. Перепечатка с издания 1984 г. – М.: ООО ИД «Альянс», 2007. – 352 с.

Все статьи автора «Снежкина Ольга Викторовна»