Введение
Метод имитационного моделирования является одним из современных методов исследования процесса обучения [2, 3]. Он состоит в построении сначала математической, а затем компьютерной модели дидактической системы и проведении с ней серии вычислительных экспериментов при различных условиях с целью установления или обоснования закономерностей обучения [1, 4].
Рассмотрим ученика, который характеризуется набором параметров, и учителя, владеющего несколькими методами обучения. Основная задача дидактики состоит в том, чтобы так выбрать методы и так распределить изучаемый материал в течение времени обучения, чтобы в конце его ученик справился с заданной системой тестов. Пусть изучаемая тема состоит из N логически связанных между собой элементов учебного материала (ЭУМ), которые следуют друг за другом. Сложность S самого простого ЭУМ будем считать равной 1, тогда для более сложных ЭУМ S больше 1. Уровень требований, предъявляемых учителем, будем рассчитывать по формуле: Tr = S_1 + S_2 + … + S_N. Если все N ЭУМ имеют сложность 1, то Tr = N. Сформулируем закон дидактики: скорость увеличения знаний Zn пропорциональна усилиям F(t) ученика, прилагаемым в единицу времени, эффективности методики обучения E, коэффициентам усвоения a и понимания П: dZn/dt=a*П*Е*F(t). Усилия F, прилагаемые учеником, характеризуют интенсивность его мыслительной деятельности и пропорциональны мотивации M; они зависят от разности между уровнем требований Tr учителя и знаниями ученика Zn.
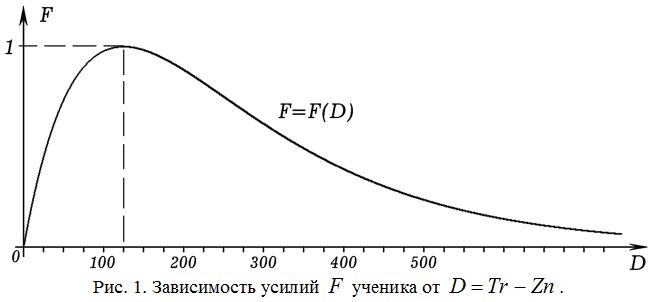
1. Зависимость усилий ученика от уровня требований учителя
Движущей силой учебной деятельности ученика является противоречие между требуемым и имеющимся у него уровнями знаний. Когда разность Tr – Zn невелика, мотивация ученика M и затрачиваемые усилия F примерно пропорциональны Tr – Zn; ученик понимает, что требования учителя разумны и соответствуют его возможностям. Если уровень требований Tr учителя существенно превосходит количество знаний ученика Zn, то ученик осознает, что не сможет в полной мере справиться с предъявляемыми заданиями. При этом мотивация M и прилагаемые усилия F уменьшаются, стремясь к 0. Существует оптимальное значение разности Tr – Zn, при котором F достигает максимума. Задача учителя состоит в нахождении оптимального уровня требований Tr, при котором ученик будет прилагать максимальные усилия F.
Зависимость усилий F ученика от разности D = Tr – Zn можно выразить функцией F(D)=4(1–exp(–r*D))*exp(–r*D), где r =1/180. Ее график представлен на рис. 1. Видно, что по мере увеличения разности Tr – Zn величина F (мотивация M) сначала увеличивается, при Tr –Zn = 125 достигает максимума, а потом уменьшается до 0, так как снижается уверенность в собственных силах.
Процесс усвоения и запоминания сообщаемой информации состоит в установлении ассоциативных связей между новыми и имеющимися у человека знаниями. При этом приобретенные знания становятся более прочными и забываются значительно медленнее, превращаясь в умения и навыки [5]. Важным условием обучения является понимание учеником изучаемого материала. Как установили психологи, человек понимает сообщаемую ему информацию, если он в состоянии соотнести ее с собственной категориальной системой понятий [5, с. 97-100]. В его сознании происходит перекодирование поступающей речевой или текстовой информации, ее “укладывание” в собственную понятийную систему с последующим запоминанием. Если ученик понял материал, то он может изложить его собственными словами.
2. Математическая и компьютерная модели обучения
Рассмотрим трехкомпонентную модель обучения “знания–умения– навыки” [2, 3]:
где Tr – уровень требований, предъявляемый учителем, Z, U и N – количества непрочных знаний, умений и навыков (то есть прочных знаний) ученика. Они отличаются прочностью усвоения и имеют коэффициенты забывания gZ, gU, gN, причем gZ > gU > gN. Коэффициенты усвоения aZ, aU, aN характеризуют быстроту усвоения знаний учеником и перехода непрочных знаний в прочные (то есть скорость формирования умений и навыков). Пока происходит обучение k = 1, а когда оно прекращается k = 0. Коэффициент забывания – величина обратная времени, в течение которого количество данного вида знаний уменьшается в e = 2,72… раза. Результат обучения характеризуется суммарным уровнем приобретенных знаний Zn = Z + U + N и коэффициентом прочности Pr = (U/2+N)/Zn. При изучении одной темы у учащегося растет количество непрочных знаний Z, одновременно с этим происходит увеличение количества умений U и навыков N (то есть прочных знаний), повышается прочность Pr. Для имитационного моделирования обучения используется программа 1.
3. Результаты моделирования
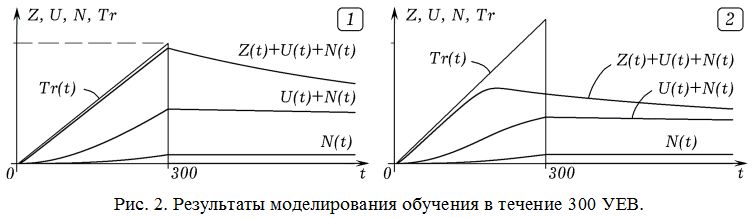
Промоделируем следующую ситуацию. Пусть в промежутке от 0 до 300 УЕВ (усл. ед. времени) ученик должен понять и запомнить последовательность взаимосвязанных рассуждений (например, вывод формулы, решение сложной задачи). В момент t’=300 УЕВ, соответствующий окончанию обучения, осуществляется контроль его знаний Zn. Во время обучения скорость поступления информации от учителя V = dTr/dt остается постоянной, причем в каждый момент учитель требует знания всего предыдущего материала. При этом уровень требований учителя растет по закону: Tr = V*t. Определим количество усвоенных учеником знаний Zn(t’) и коэффициент эффективности обучения K=Zn(t’)/(V*T) при различных V.
Результаты моделирования обучения при V=10 и 13 (скорость передачи информации V измеряется в 1/УЕВ) представлены на рис. 2. Видно, что при малых скоростях поступления информации (рис. 2.1) ученик успевает следить за рассуждениями учителя и усваивает практически все элементы учебного материала. При этом К сразу после обучения выше 0,95. После обучения происходит забывание, Zn уменьшается. В случае, когда скорость поступления учебной информации превышает некоторое пороговое значение (рис. 2.2), ученик не успевает понять ход рассуждений учителя и “отрывается” от него. Это приводит к снижению мотивации и уменьшению усилий, прилагаемых учеником, который чувствует, что все равно не сможет понять данную тему. Поэтому количество усвоенных знаний Zn и коэффициент эффективности обучения К в конце обучения оказываются существенно ниже.
Проведем серию вычислительных экспериментов, изменяя V от 1 до 24 при длительности обучения 200 УЕВ. Построим графики зависимостей знаний ученика Zn и эффективности обучения K от скорости передачи информации V (рис. 3). Из них видно, следующее: 1) при V < 11 количество усвоенных знаний Zn увеличивается прямо пропорционально V, эффективность обучения K высокая (около 0,97) и остается постоянной; 2) при V > 12 количество усвоенных знаний Zn и эффективность обучения K резко падают; 3) существует оптимальная скорость подачи информации (около 11,5), при которой количество знаний Zn, усвоенных учеником, достигает максимума. Если изучаемый материал состоит из логически несвязанных вопросов, которые могут быть изучены независимо друг от друга, то рассмотренные выше рассуждения следует провести для каждого вопроса отдельно.
При обучении между учителем (или учебником) и учеником возникает канал связи имеющий определенную пропускную способность. Скорость передачи информации V зависит от уровня требований Tr, то есть от числа N новых ЭУМ, поступающих в единицу времени, и их сложности S_i (i=1, 2, …, N). Чем сложнее утверждение учителя или записанная им формула, тем больше мыслительных действий должен совершить ученик, чтобы ее понять. Если учитель быстро излагает сложный материал, перескакивая через какие-то элементарные рассуждения, представляющие трудность для ученика, то ученик не сможет или не успеет связать сообщаемую ему новую информацию с собственной системой понятий и не поймет до конца всех проводимых рассуждений. Полученные результаты хорошо согласуются со второй теоремой Шеннона о передаче информации по каналу связи с шумом: Если скорость передачи не превышает пропускной способности канала связи с шумом, то всегда найдется способ кодирования, при котором сообщение будет передаваться с требуемой достоверностью (то есть ученик поймет сообщаемую информацию). Можно сформулировать и обратное утверждение: если производительность источника превышает пропускную способность канала связи с шумом, то не существует никакого метода кодирования позволяющего безошибочно передать сообщение. В этом случае ученик не поймет учителя и не сможет усвоить проводимые им рассуждения.
Заключение
В настоящей статье предложена трехкомпонентная модель обучения “знания–умения–навыки”, учитывающая сложную связь между усилиями ученика и разностью между требованиями учителя и уровнем знаний ученика. Установлено, что данная модель позволяет объяснить скачкообразный характер зависимости степени усвоения темы от скорости изложения материала. Это связано с тем, что при слишком большой скорости поступления новой информации ученик не успевает следить за ходом мысли и “отрывается” от учителя. В результате последующая информация усваивается существенно хуже, ученик не понимает изучаемую тему. График зависимости коэффициента усвоения от скорости подачи информации имеет ярко выраженный спад, соответствующий границе между двумя состояниями, когда ученик понял и усвоил изучаемый материал или не смог этого сделать.
Библиографический список
- Атанов Г.А., Пустынникова И.Н. Обучение и искусственный интеллект, или Основы современной дидактики высшей школы. – Донецк: Изд–во ДОУ, 2002. – 504 с.
- Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения: монография. – Глазов: Глазов. гос. пед. ин–т, 2014. – 141 с. URL: http://maier-rv.glazov.net
- Майер Р.В. Многокомпонентная модель обучения и ее использование для исследования дидактических систем // Фундаментальные исследования: Педагогические науки. 2013. N 10. С. 2524 – 2528.
- Новиков Д.А. Закономерности итеративного научения. – М.: Институт проблем управления РАН, 1998. – 77 с.
- Фридман Л.М., Кулагина И.Ю. Психологический справочник учителя. – М.: Просвещение. – 1991. – 288 с.