Ионообменную сорбцию изучали на модельных водных растворов CuSO4 с концентрацией по меди 0,01-0,8 моль·кг-1 при температуре 298 К. Величину ионообменной сорбции Г (моль·кг-1) катионов меди определяли в статических условиях при отношении объема жидкой фазы к массе твердой V/m=10 мл·г-1 и массе навески ЖМК 5 г, при скорости перемешивания 400 об·мин-1 до равновесного состояния.
В таблице 1. приведены исходные и равновесные концентрации ионов меди C0 и Cр; равновесные концентрации ионов натрия CNa+; ионная сила раствора I;величины ионообменной сорбции Г моль·кгˉ¹ и обратные величины ионообменной сорбции ионов меди 1/Г мольˉ¹·кг; средние ионные коэффициенты активностиγ± Na2SO4 и CuSO4, взятые из табличных данных [1].
Таблица 1.Результаты опытов по ионообменной сорбции катионов Cu2+ и Na+ на ЖМК
|
С0,
молькг-1 |
Ср,
молькг-1 |
СNa+,
молькг-1 |
I
|
Г, моль·кгˉ¹
|
1/Г
|
γ±
Na2SO4[1] |
γ±
CuSO4[1] |
|
0,01
|
4,97·10-9
|
0,020
|
0,030
|
0,100
|
10
|
0,718
|
0,509
|
|
0,03
|
7,15·10-6
|
0,060
|
0,090
|
0,300
|
3,334
|
0,590
|
0,297
|
|
0,05
|
2,28·10-5
|
0,100
|
0,150
|
0,500
|
2,001
|
0,539
|
0,231
|
|
0,07
|
2,86·10-4
|
0,139
|
0,210
|
0,697
|
1,434
|
0,523
|
0,196
|
|
0,10
|
7,50·10-3
|
0,185
|
0,307
|
0,925
|
1,082
|
0,456
|
0,162
|
|
0,20
|
9,41·10-2
|
0,212
|
0,694
|
1,059
|
0,944
|
0,340
|
0,109
|
|
0,30
|
1,77·10-1
|
0,246
|
1,077
|
1,230
|
0,813
|
0,290
|
0,088
|
|
0,40
|
2,70·10-1
|
0,260
|
1,470
|
1,302
|
0,768
|
0,259
|
0,075
|
|
0,80
|
6,27·10-1
|
0,346
|
3,027
|
1,730
|
0,578
|
0,200
|
0,053
|
На рисунке 1 приведена изотерма ионообменной сорбции катионов Cu2+ на ЖМК на основании данных таблицы 1. Измерения равновесной концентрации ионов Na+ с помощью ионоселективного электрода подтвердили эквивалентность обмена катионов Na+ на катионы Cu2+. Изотерма на рисунке 1 описывается уравнением Фрейндлиха: Г=1,763Ср0,142 с достоверностью аппроксимации R2 = 0,97.
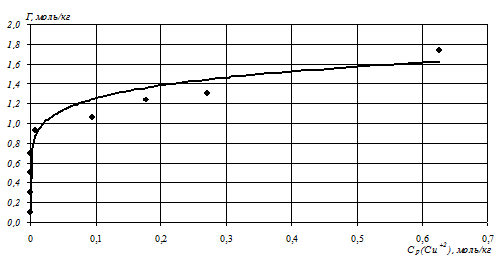
Рисунок 1. Изотерма ионообменной сорбции катионов Cu2+ и Na+ на ЖМК
Термодинамическое описание изотермы ионообменной сорбции катионов Cu2+ и Na+ было проведено при допущении идеальности твердой фазы, т.е. без учета коэффициентов активности ионов в сорбированном состоянии [2]. Использовали метод линеаризации уравнения, полученного преобразованием уравнения закона действующих масс для реакции:
Приведенная к виду
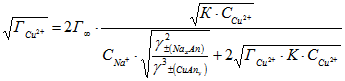 (1)
(1)
Линейная форма уравнения имеет вид:
.gif) , (2)
, (2)
Зависимость обратной величины сорбции ионов Cu2+ ![]() от аргумента
от аргумента 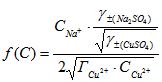 приведена на рисунке 2.
приведена на рисунке 2.
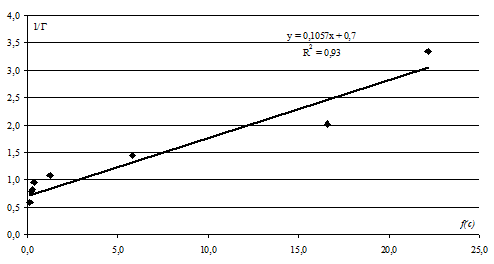
Рисунок 2. Линейная форма изотермы ионообменной сорбции катионов Cu2+ и Na+ на ЖМК.
Зависимость аппроксимируется линейным уравнением: ![]()
![]() с достоверностью аппроксимации R2 = 0,93.
с достоверностью аппроксимации R2 = 0,93.
По угловому коэффициенту вычислено значение предельной сорбции ионов Cu2+ ![]() = 1,43 моль·кг-1. Кажущуюся константу ионообменной сорбции катионов Cu2+ и Na+
= 1,43 моль·кг-1. Кажущуюся константу ионообменной сорбции катионов Cu2+ и Na+ ![]() = 43,8±0,5 и энергию Гиббса ионообменной сорбции катионов Cu2+ и Na+ на ЖМК
= 43,8±0,5 и энергию Гиббса ионообменной сорбции катионов Cu2+ и Na+ на ЖМК ![]() –9,3±0,48 кДж·моль-
–9,3±0,48 кДж·моль-
По величине удельной поверхности ЖМК Sуд = 43,81 м2·г-1 [3] и предельной сорбции катионов Cu2+ 1,43 молькг-1 была оценена «посадочная площадка» ионов Cu2+:
![]() =
=![]() м2. (3)
м2. (3)
По величине «посадочной площадки» вычислили радиус сорбированного катиона Сu2+, равный 127 пм. Данное значение больше значения кристаллографического радиуса Сu2+ по Бокию 80 пм [1] и меньше радиуса, вычисленного по уравнению Стокса 324 пм:
![]() , (4)
, (4)
где ![]() - заряд катиона меди, F – постоянная Фарадея, η – вязкость воды,
- заряд катиона меди, F – постоянная Фарадея, η – вязкость воды, ![]() - предельная эквивалентная электропроводность катиона меди.
- предельная эквивалентная электропроводность катиона меди.
Следовательно, катион Сu2+ сорбируется на ЖМК в частично дегидратированном состоянии.
Выводы
1. Изотерма сорбции катионов Cu2+ на катионы Na+ на поверхности ЖМК описывается уравнением, полученным преобразованием уравнения закона действующих масс, и может быть представлена в линейном виде:
2. Определена кажущиеся константа ионообменной сорбции![]()
3. Рассчитано значение предельной сорбции ионов Cu2+
![]() 1,43 моль·кг-1
1,43 моль·кг-1
4. Получены значения дифференциальной энергия Гиббса ионообменной сорбции для ионов Cu2+
5. Оценены посадочная площадка и значение радиуса сорбированных катионов:
6. Радиусы сорбированных катионов имеют значения, промежуточные между кристаллографическими радиусами катионов по Бокию и радиусами гидратированных катионов в водном растворе по Стоксу, что соответствует представлению о сорбции катионов на поверхности ЖМК в слое Штерна–Гельмгольца в частично дегидратированном состоянии.
Результаты были получены в рамках выполнения государственного задания Минобрнауки России по проекту № 982 «Развитие термодинамической и кинетической теории межфазного ионного обмена применительно к природным и промышленным объектам» от 11.06.2014г.
Библиографический список
- Краткий справочник физико-химических величин./ Под ред. А.А. Равделя и А.М. Пономаревой. Л.: Химия. 2002. С. 123, 130, 200. 232 231 с.
- Зарицкий В.П. // Конкреции и конкреционный анализ: Сб. статей. М.: Наука, 1977. С 84-89, 245 с.
- Чиркст Д.Э., Черемисина О.В., Иванов М.В., Чистяков А.А., Жадовский И.Т., /Изотерма обмена катионов стронция и натрия на железомарганцевых конкрециях // ЖПХ. 2006. Т. 79. № 3. С.374-379.
