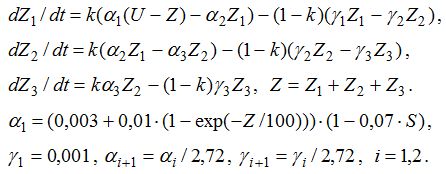Введение
Одно из направлений развития современной дидактики заключается в использовании математических и имитационных (компьютерных) моделей для изучения процесса обучения [1–9]. Метод имитационного моделирования позволяет исследователю изучать сложные объекты и процессы в случае, когда проводить реальные эксперименты с ними невозможно или нецелесообразно. Сущность этого метода состоит в построении компьютерной модели реальной системы и проведении серии вычислительных экспериментов с целью понимания поведения системы или оценки различных стратегий управления, обеспечивающие ее функционирование [10, c. 12]. Процесс создания имитационной модели Р.Шеннон называет “интуитивным искусством” или “искусством моделирования”, которое “состоит в способности анализировать проблему, выделять из нее путем абстракции ее существенные черты, выбирать и должным образом модифицировать основные предположения, характеризующие систему, а затем отрабатывать и совершенствовать модель до тех пор, пока она не станет давать полезные для практики результаты” [10, c. 34].
Известные модели процесса обучения [1–5, 9] обладают существенным недостатком: они не учитывают, что при многократном использовании учащимся ранее изученных элементов учебного материала (ЭУМ) эти знания усваиваются более прочно и забываются медленнее. Но ведь именно этот процесс повышения прочности усвоенных знаний при их использовании учеником в своей деятельности и лежит в основе формирования умений и навыков, которые сохраняются длительное время. Как говорил Б.Ф. Скиннер, “образование – это то, что остается, когда все выученное забыто.” Данное высказывание можно перефразировать так: образование – это прочные знания, полученные своим трудом за счет их многократного использования, остающиеся у человека после того, как он забыл все непрочные знания, которые не были включены в его учебную деятельность.
В настоящей статье рассматриваются два типа моделей, учитывающих повышение прочности знаний при обучении: 1) многокомпонентная непрерывная модель обучения, учитывающая переход непрочных знаний в прочные; 2) непрерывная модель обучения с изменяющимся коэффициентом забывания. В работе представлены компьютерные программы, написанные на языке Visual Basic в среде Excel, и конкретные результаты моделирования.
1. Многокомпонентная непрерывная модель обучения
Обозначим через U уровень требований, предъявляемый учителем. Он равен (или пропорционален) количеству рассматриваемых ЭУМ, которые должен усвоить учащийся. Суммарные знания ученика Z включают в себя непрочные знания первой категории, более прочные знания второй категории и очень прочные знания третьей категорий: Z=Z_1+Z_2+Z_3 [6, 7]. В процессе обучения (k=1) сообщаемая учителем информация сначала превращается в знания первой категории, а затем в результате ее использования при выполнении учебных заданий – в знания второй и третьей категории (рис. 1.1). При этом прочность усваиваемого материала постепенно возрастает. Скорость перехода непрочных знаний в разряд более прочных знаний характеризуется коэффициентами усвоения.
При отсутствии обучения (k=0) происходит обратный переход: часть прочных знаний третьей категории постепенно становятся менее прочными знаниями второй категории, те в свою очередь частично переходят в разряд непрочных знаний первой категории, которые забываются. Скорости переходов знаний (i–1)–ой категории в знания i–ой категории и наоборот при обучении и забывании характеризуется коэффициентами усвоения и забывания, которые отличаются друг от друга в e = 2,72… раза. Таким образом, в основу предлагаемой модели положены следующие принципы:
1. Сообщаемая учащимся информация (знания) является совокупностью равноправных несвязанных между собой элементов учебного материала (ЭУМ), число которых пропорционально ее количеству.
2. В процессе обучения учащийся оперирует имеющейся у него информацией, выполняя различные учебные задания. При этом сообщаемые учителем знания сначала усваиваются непрочно (становятся знаниями первой категории), затем по мере их повторения и использования – прочнее (превращаются в знания второй категории), а затем становятся прочными (знания третьей категории).
3. Скорость увеличения непрочных знаний ученика в процессе обучения пропорциональна разности между уровнем требований учителя U (который равен количеству сообщаемых им знаний) и суммарными знаниями ученика Z.
4. Во время обучения скорость превращения непрочных знаний в прочные пропорциональна количеству непрочных знаний.
5. При отсутствии обучения происходит забывание: знания становятся менее прочными и постепенно забываются. Скорость уменьшения прочных или непрочных знаний ученика при забывании пропорциональна количеству этих знаний.
6. Коэффициент усвоения ученика тем выше, чем больше количество усвоенных им знаний Z и чем меньше сложность S изучаемого материала.
Предлагаемая трехкомпонентная модель обучения выражается системой уравнений (при обучении k=1; при забывании k=0):
Результат обучения характеризуется суммарным уровнем приобретенных знаний Z и коэффициентом прочности Pr=(Z_2/2+Z_3)/Z. Если все приобретенные во время обучения знания непрочные (Z_1=Z, Z_2=Z_3=0), то коэффициент прочности Pr=0. Надо стремиться к ситуации, когда все приобретенные знания прочные (Z_3=Z, Z_1=Z_2=0), тогда Pr=1. При длительном изучении одной темы уровень знаний Z увеличивается до U, одновременно с этим происходит повышение доли прочных знаний Z_3, растет прочность Pr.
Программа ПР–1.
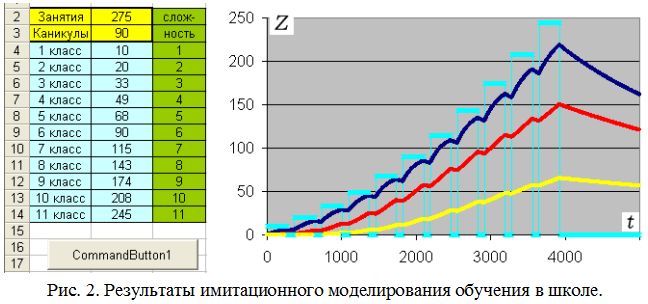
Для имитационного моделирования одиннадцатилетнего обучения в школе используется программа ПР–1; результаты представлены на рис 2. Предполагается, что в течение учебного года школьник 275 дней учится, а 90 дней отдыхает на летних каникулах. Уровень требований учителя U и сложность учебной информации S с каждым годом увеличиваются (рис. 2). В программе ПР–2 используется коэффициент 0,07, поэтому сложность растет от 0,07 до 0,77. Коэффициенты усвоения и забывания подобраны так, чтобы график суммарных знаний Z(t) (синяя линия) примерно соответствовал бы достаточно успешному ученику, который усваивает 70–90 процентов требуемой информации (рис. 2). Желтая линия соответствует знаниям первой категории, а красная –– сумме знаний первой и второй категорий. По оси абсцисс откладывается время (в днях), прошедшее с момента поступления ученика в школу.
2. Модель обучения с изменяющимся коэффициентом забывания
Другой подход заключается в учете того факта, что при увеличении числа обращений ученика к конкретному ЭУМ (вопросу, задаче) коэффициент забывания этого ЭУМ уменьшается. Допустим, что ученик в процессе обучения вынужден решать однотипных задач по одной и той же теме. Во время урока он в определенные моменты времени складывает числа (или читает отдельные слова, выполняет задания теста). Остальное время на уроке он занимается другой учебной деятельностью, которая нас пока не интересует. В основе предлагаемой модели [8] лежат следующие утверждения:
1. Учебный курс состоит из N независимых одинаковых по объему и сложности элементов учебного материала (ЭУМ), к которым ученик обращается в случайной или заданной последовательности. В каждый момент времени ученик может работать не более чем с одним ЭУМ.
2. Ученик неоднократно обращается к каждому ЭУМ. При каждом обращении ученика к i–тому ЭУМ его уровень знаний Z(i) i–того ЭУМ возрастает до 1.
3. После окончания работы с i–тым ЭУМ ученик начинает его забывать. Его уровень знаний Z(i) убывает по экспоненциальному закону, скорость которого определяется коэффициентом забывания gamma(i).
4. Каждому ЭУМ соответствует свой коэффициент забывания. При увеличении числа s(i) обращений ученика к i–тому ЭУМ коэффициент забывания gamma_i уменьшается.
5. По мере увеличения числа s(i) обращений ученика к i–тому ЭУМ время работы ученика с i–тым ЭУМ уменьшается, стремясь к некоторому пределу, который равен минимально возможному времени работы с данным ЭУМ.
6. Суммарное количество знаний в каждый момент времени равно сумме знаний учеником каждого ЭУМ: Z=Z(1)+Z(2)+…+Z(N).
При этом используются формулы:
Программа ПР–2.
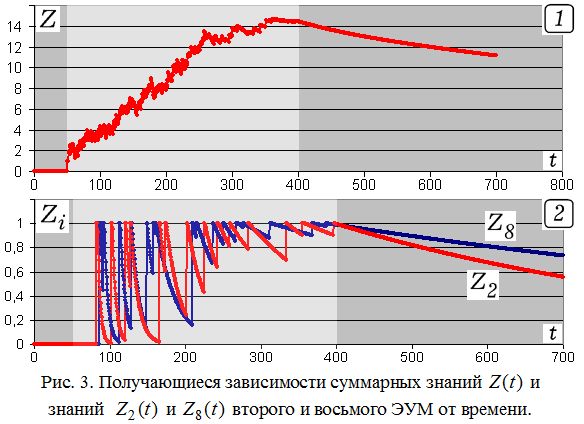
Для моделирования используется программа ПР–2; с ее помощью можно построить графики: 1) зависимости суммарных знаний Z от времени t (рис. 3.1); 2) зависимости среднего времени работы по всем ЭУМ от времени t [8]; 3) зависимости среднего коэффициента забывания по всем ЭУМ от времени t; 4) уровня знаний одного или нескольких ЭУМ от времени t (рис. 3.2). Для графиков на рис. 3 число ЭУМ N=15, а время обучения T=350 УЕВ. Видно, что во время обучения суммарное количество знаний возрастает, а после окончания –– убывает из–за забывания. В случае, когда к некоторому ЭУМ ученик обращается несколько раз, происходит уменьшения скорости забывания; после каждого обращения этот ЭУМ забывается все медленнее и медленнее (рис. 3.2).
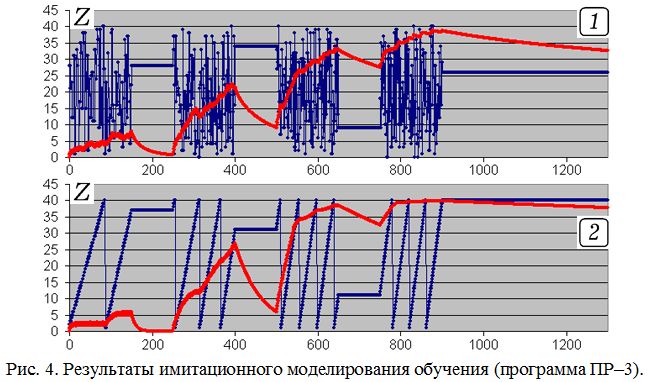
Теперь промоделируем изучение N=40 ЭУМ в течение 4 занятий продолжительностью T=150 УЕВ. Занятия разделены перерывами длительностью T_n=100 УЕВ. Во время обучения ученик обращается то к одному, то к другому ЭУМ с равными вероятностями. По мере роста числа s_i обращений к i–ому ЭУМ уменьшается затрачиваемое время tau_i и коэффициент забывания gamma_i. Используется программа ПР–3, результаты имитационного моделирования представлены на рис. 4.1. Видно, что во время обучения номер i изучаемого ЭУМ изменяется случайно от 1 до 40, суммарный уровень знаний ученика (переменная SZ) при этом увеличивается. Во время перерывов происходит забывание, суммарный уровень знаний ученика SZ уменьшается. На рис. 4.2 представлены результаты моделирования для случая, когда ЭУМ изучаются по порядку. Видно, что из–за уменьшения времени работы с каждым ЭУМ на первом занятии ученик не успевает рассмотреть все ЭУМ даже два раза, а в течение четвертого занятия успевает поработать с большей частью ЭУМ четыре раза.
Программа ПР–3.
Заключение
В статье рассмотрены два принципиально различных способа моделирования процесса обучения, которые учитывают изменение прочности знаний при обучении и забывании. Первый подход предполагает построение непрерывной модели, основанной на численном решении системы дифференциальных уравнений. Она исходит из того, что: 1) прочность усвоения различных ЭУМ неодинакова; 2) прочные знания забываются существенно медленнее непрочных; 3) непрочные знания при их использовании учащимся постепенно становятся прочными; 4) при отсутствии обучения прочные знания становятся непрочными. Второй подход заключается в построении дискретной модели, которая учитывает, что при увеличении числа обращений ученика к данному элементу учебного материала: 1) время его использования уменьшается, стремясь к некоторому пределу; 2) коэффициент забывания уменьшается, стремясь к нулю. Результаты моделирования хорошо согласуются с основными выводами теории обучения.
Библиографический список
- Добрынина Н.Ф. Математические модели распространения знаний и управления процессом обучения студентов. – Фундаментальные исследования. –2009. – N 7. – С. 7–9
- Доррер А.Г., Иванилова Т.Н. Моделирование интерактивного адаптивного обучающего курса // Современные проблемы науки и образования. – 2007. – N 5.
- Ивашкин Ю.А., Назойкин Е.А. Мультиагентное имитационное моделирование процесса накопления знаний // Программные продукты и системы. – 2011. – N 1. – С. 47 – 52.
- Кудрявцев В.Б., Вашик К., Строгалов А.С., Алисейчик П.А., Перетрухин В.В. Об автоматном моделировании процесса обучения. – Дискретная математика. – 1996. – Т. 8., вып. 4. – С. 3 – 10.
- Леонтьев Л.П., Гохман О.Г. Проблемы управления учебным процессом: Математические модели. – Рига, 1984. – 239 с.
- Майер Р.В. Двухкомпонентная модель изучения курса: результаты имитационного моделирования // Психология, социология и педагогика. 2014. № 11 [Электронный ресурс]. URL: http://psychology.snauka.ru/2014/11/3835.
- Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения. – Глазов, ГГПИ, 2013. – 138 c. (http://maier-rv.glazov.net)
- Майер Р.В. Компьютерная модель обучения с изменяющимся коэффициентом забывания // International Journal of Open Information Technologies – Vol 2, No 1 (2014). – pp. 12–16. (http://injoit.org/index.php/j1/article/view/59)
- Фирстов В.Е. Математические модели управления дидактическими процессами при обучении математике в средней школе на основе кибернетического подхода: Дисс. … докт. пед. наук. – С. Петербург., 2011. – 460 с.
- Шеннон Р. Имитационное моделирование систем: Искусство и наука. – М: Мир, 1978. – 418 с.