При составлении учебных программ по курсу “Математика” в любом техническом вузе межпредметным связям должно уделяться особое внимание [1,2,3,4]. Для направления подготовки“Землеустройство и кадастры” акцент рекомендуется сделать на дисциплину ”Геодезия”.
Одним из основных направлений геодезии является инженерная или прикладная геодезия. Геодезия (от греч. «землеразделение») – одна из наук о Земле, точная наука о фигуре, гравитационном поле, параметрах вращения Земли и их изменениях во времени. С другой стороны геодезия – это отрасль прикладной математики, тесно связанная с геометрией, тригонометрией, математическим анализом, теорией вероятностей, математической статистикой и вычислительной математикой. 
Геодезия как наука разрабатывает методику геодезических измерений для изысканий, проектирования, строительства и эксплуатации инженерных сооружений, выверки конструкций, наблюдений за деформациями сооружений.
В качестве примера взаимосвязи математики и геодезии рассмотрим перечень геодезических работ и применяемого математического аппарата при изыскании и проектировании линейных сооружений (рис.1).

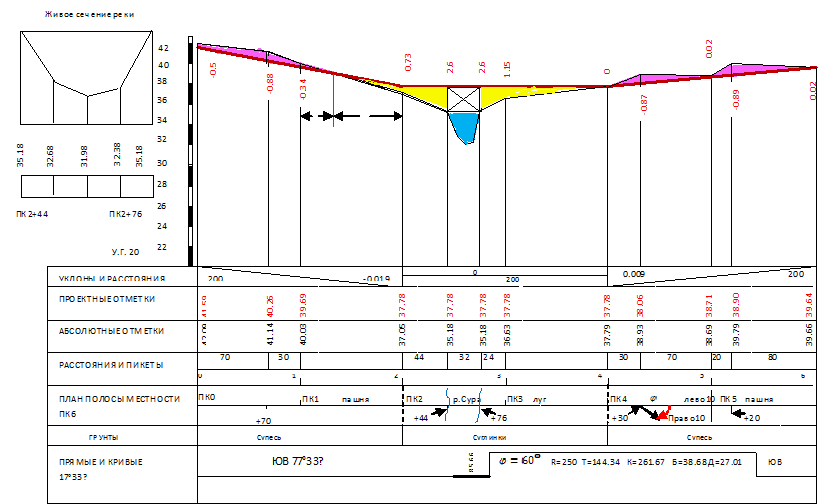
Согласно статье 1 Градостроительного кодекса Российской Федерации от 29.12.2004г. N 190-ФЗ (ГрК РФ) к линейным объектам относятся: линии электропередачи, линии связи (в том числе линейно-кабельные сооружения), трубопроводы, автомобильные дороги, железнодорожные линии и другие подобные сооружения. 
По результатам инженерно-геодезических изысканий по каждому объекту составляется технический отчёт. Графическая часть технического отсчёта по трассам линейных сооружений должна содержать продольные и поперечные профили проектируемых трасс.
Продольная ось линейного сооружения называется трассой. Задать на местности положение трассы, значит задать положение самого линейного сооружения. Продольный профиль трассы линейного объекта по заданному направлению является исходным документом для проектирования. Для получения необходимых данных для построения профиля проводится полевое трассирование, обработка результатов измерений.
Перечень геодезических работ и применяемый математический аппарат при изыскании и проектировании линейных сооружений приведем в таблице 1.

Вид работ	В чём заключается	Математический аппарат
Рекогносцировка	На местности отыскиваются точки опорной геодезической сети и осуществляется привязка к ним
Определение плюсовых точек	Определение и закрепление на местности углов поворота трассы
Разбивка пикетажа	По всей трассе последовательно откладывают отрезки длиной 100 метров и закрепляют их колышками (пикетами). Нумерация пикетов ведется от начала трассы. Первый пикет имеет номер 0.
Нивелирование трассы	Определение превышений между пикетами и реперами (как между связующими точками)	h1= aч – bчh2 =aКР - bКР
	Определение невязки нивелирного хода	ƒh=Σ h пол. –Σ Σ =  –
	Уравнивание нивелирного хода
	Определение абсолютных отметок связующих точек	где - абсолютная отметка последующей точки, - абсолютная отметка предыдущей точки, – исправленное превышение.
	Определение абсолютных отметок промежуточных точек через горизонт прибора	= НПК0 + а= НПК1 + b , где с – отсчет на промежуточную точку,– среднее значение горизонта инструмента на станции, - абсолютная отметка промежуточной точки
Расчёт элементов круговой кривой (Рис.2)	Разбивка круговой кривой сводится к плановому определению трех ее главных точек: начала кривой НК, середины кривой СК и конца кривой КК. С этой целью на трассе определяют точку поворота трассы и измеряют угол поворота трассы , также определяют радиус дуги R, который выбирается в зависимости от категорий автомобильных дорог. Рассчитываются главные элементы кривой:
	Тангенс кривой (Т) – это расстояние от вершины угла до точек касания с дугой (длина касательной).
	Длина кривой (К) – расстояние между точками касания, считываемое по кривой
	Биссектриса кривой (Б) – расстояние от вершины угла до середины кривой.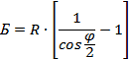
	Домер (Д) – разность расстояний, считываемых по тангенсам и по кривой	Д = 2Т – К
Расчёт пикетажа	Определение начала кривой и конца кривой	НК =ВУ – ТКК=НК + К КК = ВУ +Т – Д
Вынос пикета с тангенса на кривую	При разбивке круговых кривых пикеты с тангенса на кривую выносят методом прямоугольных координат. За ось Х, принимается тангенс кривой, а за ось Y линию перпендикулярную тангенсу.	Х =R · sin ΘY = R – R · cos Θ = R (1 – cos Θ)
Построение продольного профиля
	Определение уклонов и расстояний	, где h1 это превышение между проектными точками, d1 – расстояние между ними.
	Определение проектных отметок
	Определение рабочих отметок
	Определение расстояния до точки нулевых работ
	Определение румба направления трассы после поворота	α посл. = α пред.. +, где  - угол поворота трассы, α пред. – дирекционный уголпервоначального направления трассы

На основании приведенных расчетов, представленных в таблице 1, можно сделать вывод, что математика и геодезия неразрывно связаны друг с другом. Именно математика даёт точным естественным наукам определённую меру уверенности в выводах, достичь которой без математики они не могут (Альберт Эйнштейн).

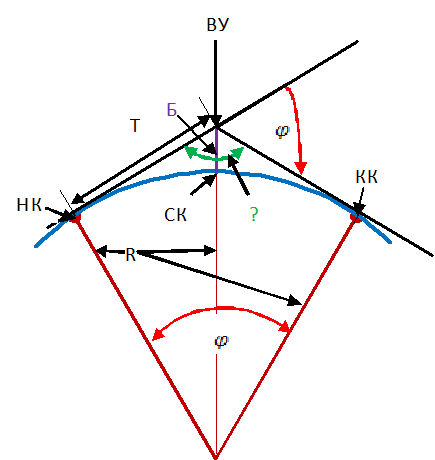
Рис.2 – Расчёт элементов круговой кривой

1. Бочкарева, О.В. Математические задачи как средство формирования профессиональных качеств личности / О.В. Бочкарева, Т.Ю. Новичкова, О.В. Снежкина, Р.А. Ладин // Современные проблемы науки и образования.–2014.–№2; URL:  http://www.science-education.ru/116-12584
2. Ладин, Р.А. Математика и междисциплинарные связи / Р.А. Ладин, О.В.Снежкина, О.В. Бочкарева, Н.В.Титова//Молодой ученый.- 2014.- № 1.- С. 550-552.
3. Шмаков, И.С. Реализация межпредметных связей / И.С. Шмаков, О.В. Снежкина, О.В. Бочкарева// Вестник магистратуры.- 2014.- № 6-1 (33).- С. 68-71.
4. Ладин, Р.А. Математика в учебном процессе строительного вуза / Р.А. Ладин, О.В. Снежкина, Г.А. Левова // Вестник магистратуры. -2013.- № 12-4 (27).- С. 56-59.

Все статьи автора «Снежкина Ольга Викторовна»