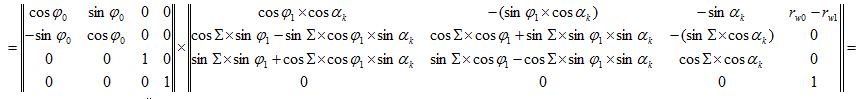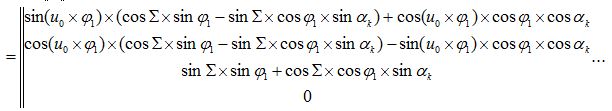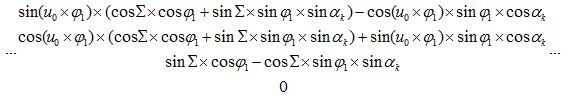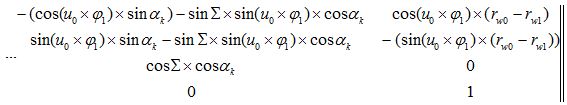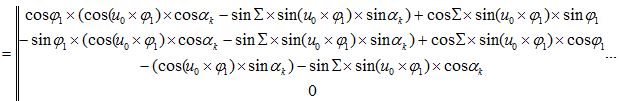Зубчатые передачи нашли широкое распространение в машинах и механизмах различных отраслей современного машиностроения.  Традиционная технология обработки резанием цилиндрических зубчатых колес основана на применении двух основных методов, а именно, метода обкатки и метода единичного деления.

Помимо упомянутых традиционных методов изготовления цилиндрических зубчатых колес, необходимо отметить метод зуботочения, впервые научно обоснованный во ВНИИИНСТРУМЕНТ [22]. Сущность этого метода заключается в том, что для его реализации используется специальный инструмент (обкаточный резец) типа косозубого долбяка с числом зубьев, равным числу заходов при согласованных вращениях инструмента и изделия на их скрещивающихся в пространстве осях. Метод в силу различных причин не получил широкого распространения. Однако, учитывая все более широкое применение современного оборудования с ЧПУ, использование данного метода в современных условиях представляется весьма перспективным.

Оборудование с ЧПУ, имея сложную кинематику работы, позволяет применять более простой инструмент. Так классический обкаточный резец можно упростить за счет изменения его конструкции, а именно принять задний угол равным нулю. Такие изменения обеспечат неизменный профиль в следствии переточки инструмента, т.е. погрешности переточки будут минимизированы.

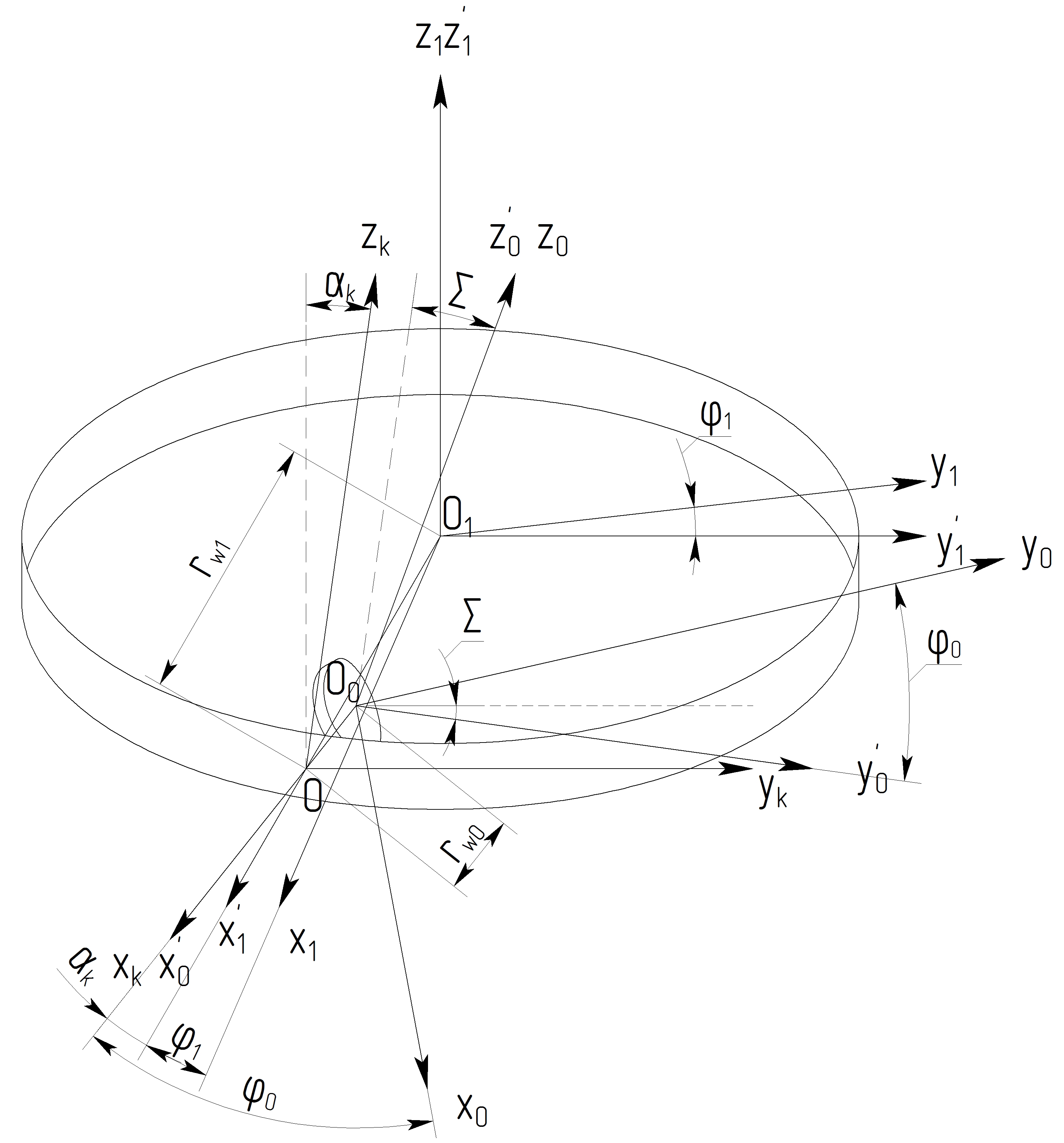
При проектирование режущего инструмента важнейшим является прямая задача профилирования, то есть определение профиля инструмента по заданному профилю детали. Для определения профиля инструмента в первую очередь  необходимо задаться системами координат определяющие внутреннее станочное зацепление, характеризующееся кинематической схемой, изображенной на рис. 1 [1].

Рисунок 1 – Схема внутреннего станочного зацепления обкаточного резца с обрабатываемой деталью

Соотношения между указанными системами координат определяются математическими зависимостями [23], выраженными матрицами четвертого порядка. Так для вывода уравнения огибающей профиля инструмента используется матрица, связывающая систему координат изделия с системой координат инструмента:

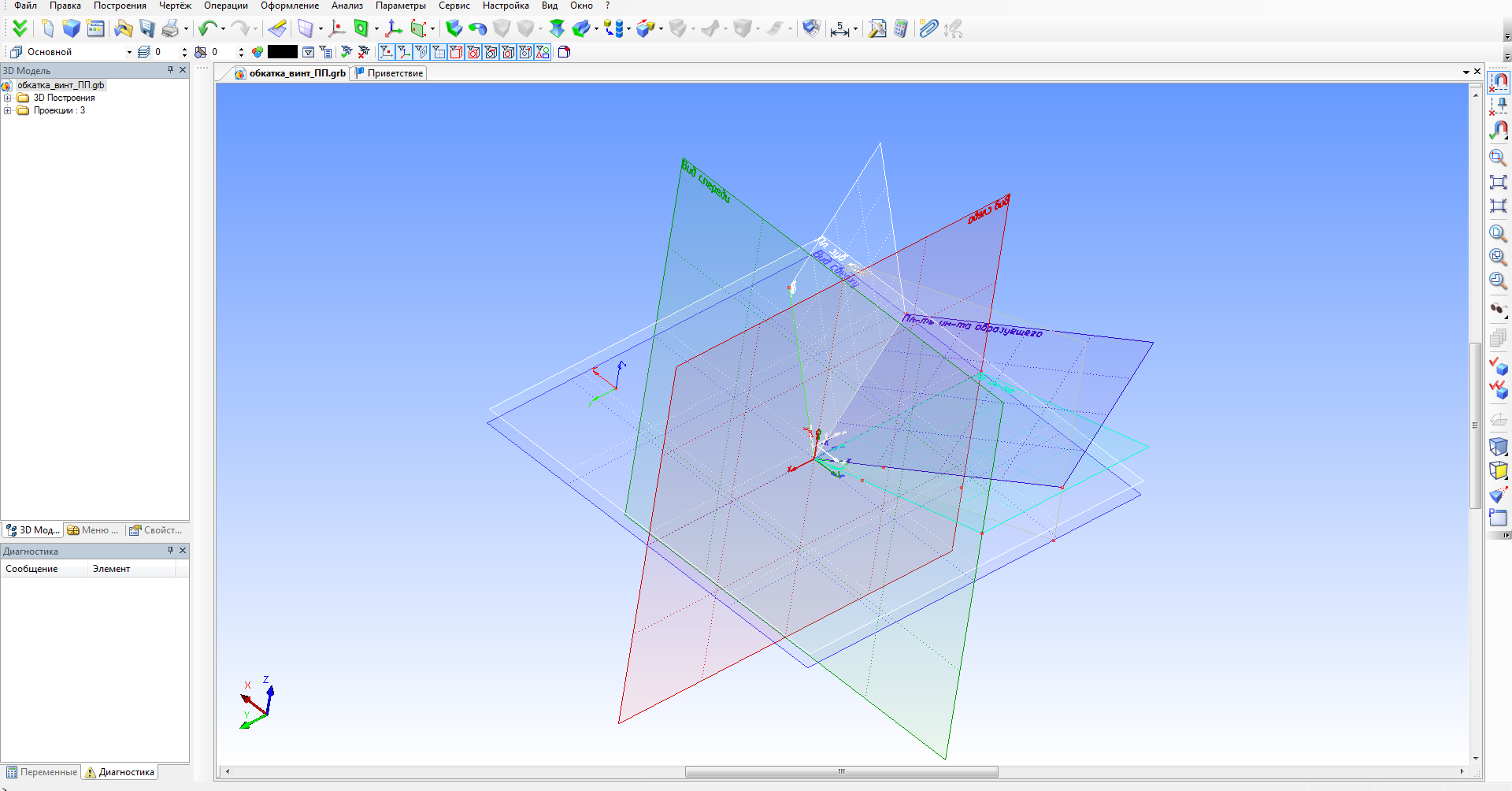
Согласно поставленной задаче, необходимо реализовать указанные системы координат в среде t-Flex CAD 3D (рис. 2).

Рисунок 2 – Системы координат, необходимые для реализации модели

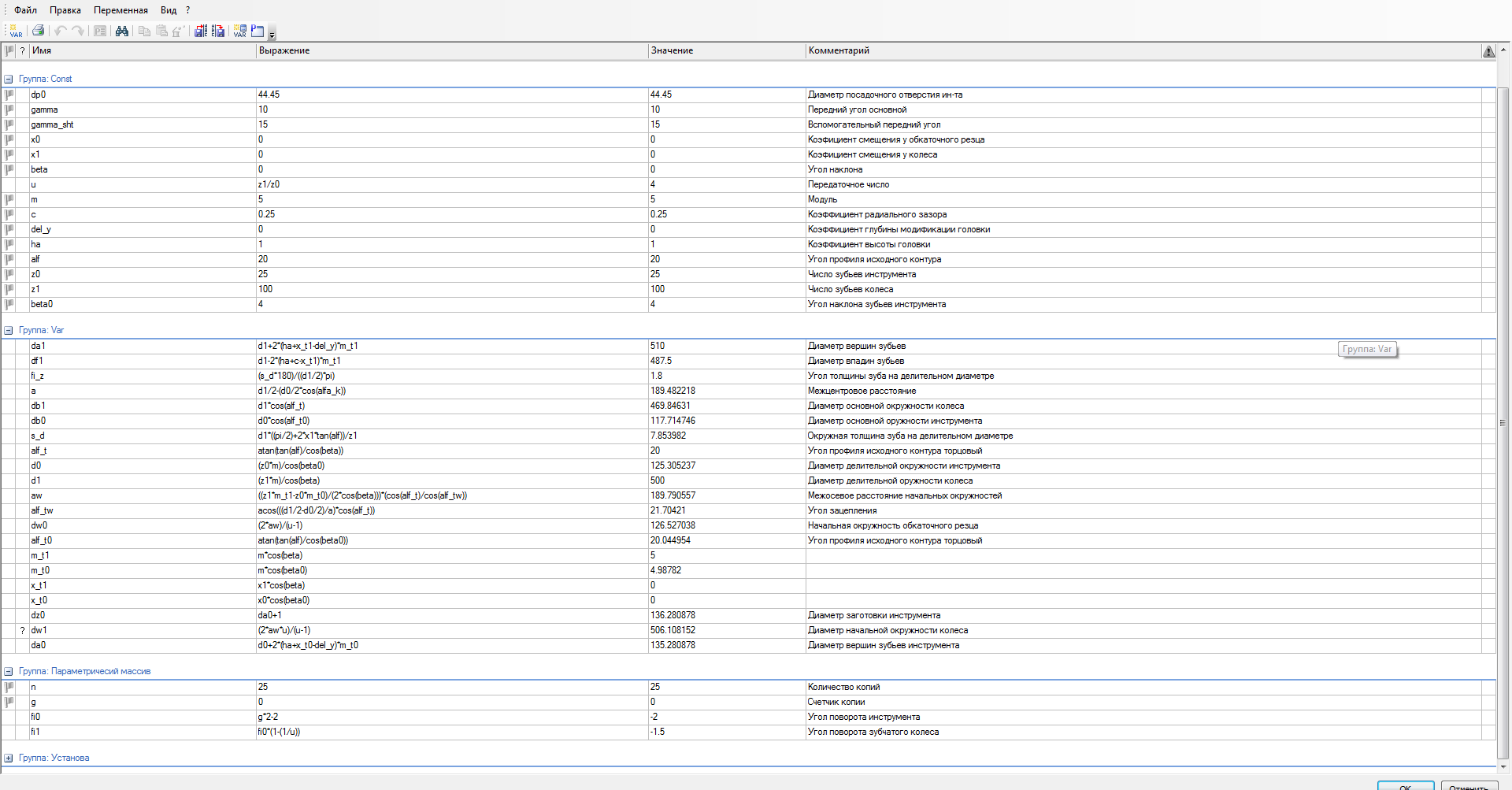
Прямая задача профилирования гласит, что профиль инструмента определяется по заданному, то есть известному, профилю детали. Обрабатываемой деталью является зубчатое колесо внутреннего зацепления. В связи с этим, в среде t-Flex CAD 3D реализуется параметрическая модель колеса внутреннего зацепления. Для этого указываются все необходимые параметры колеса (модуль, число зубьев, угол наклона зубьев, угол профиля исходного контура) и рассчитываются зависимые параметры (диаметры основной и делительной окружностей, диаметры вершин и впадин зубьев, окружные величины толщин зубьев и др.) по известным формулам [24] (рис. 3).

Рисунок 3 – Параметры модели и математические зависимости

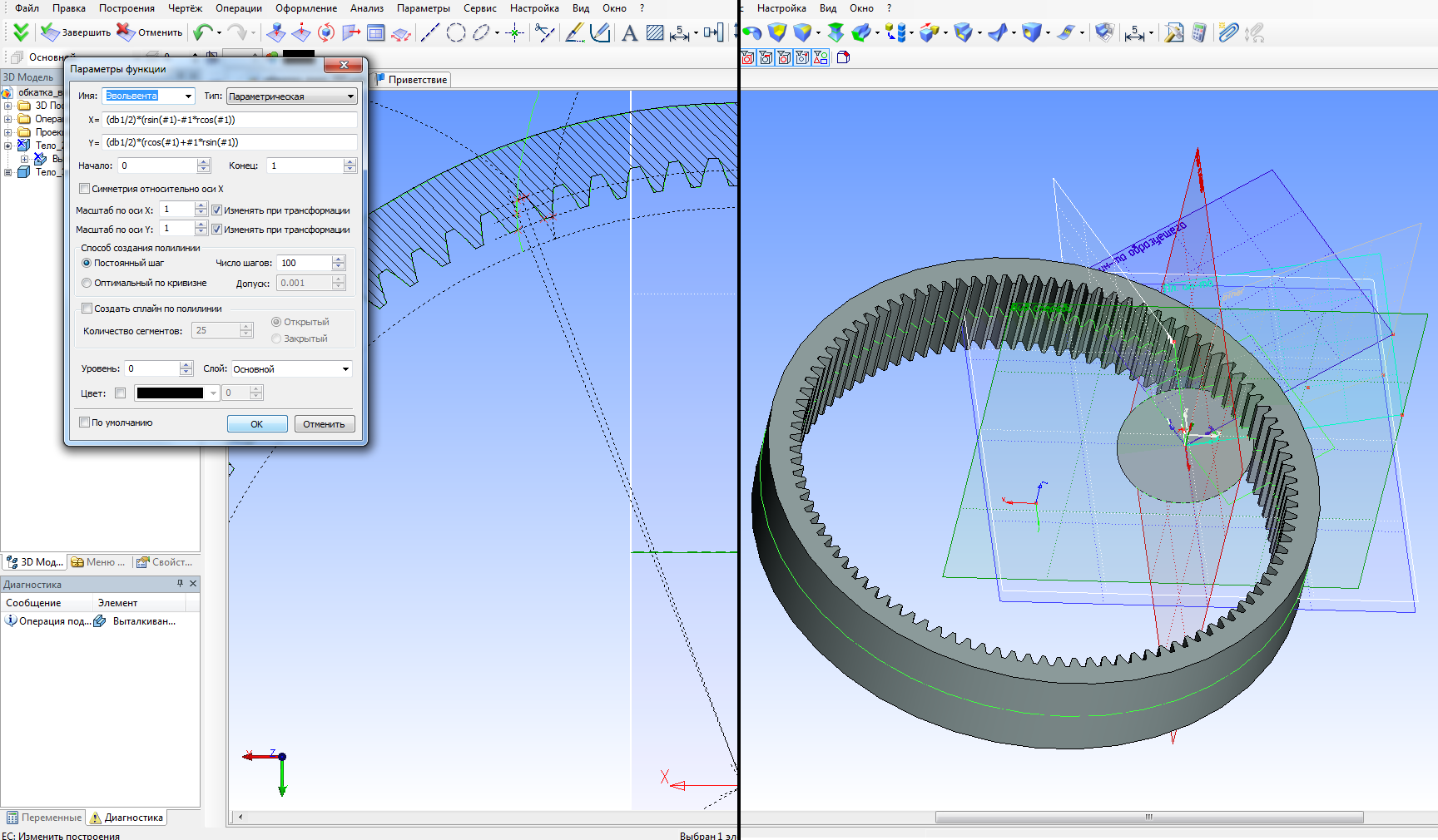
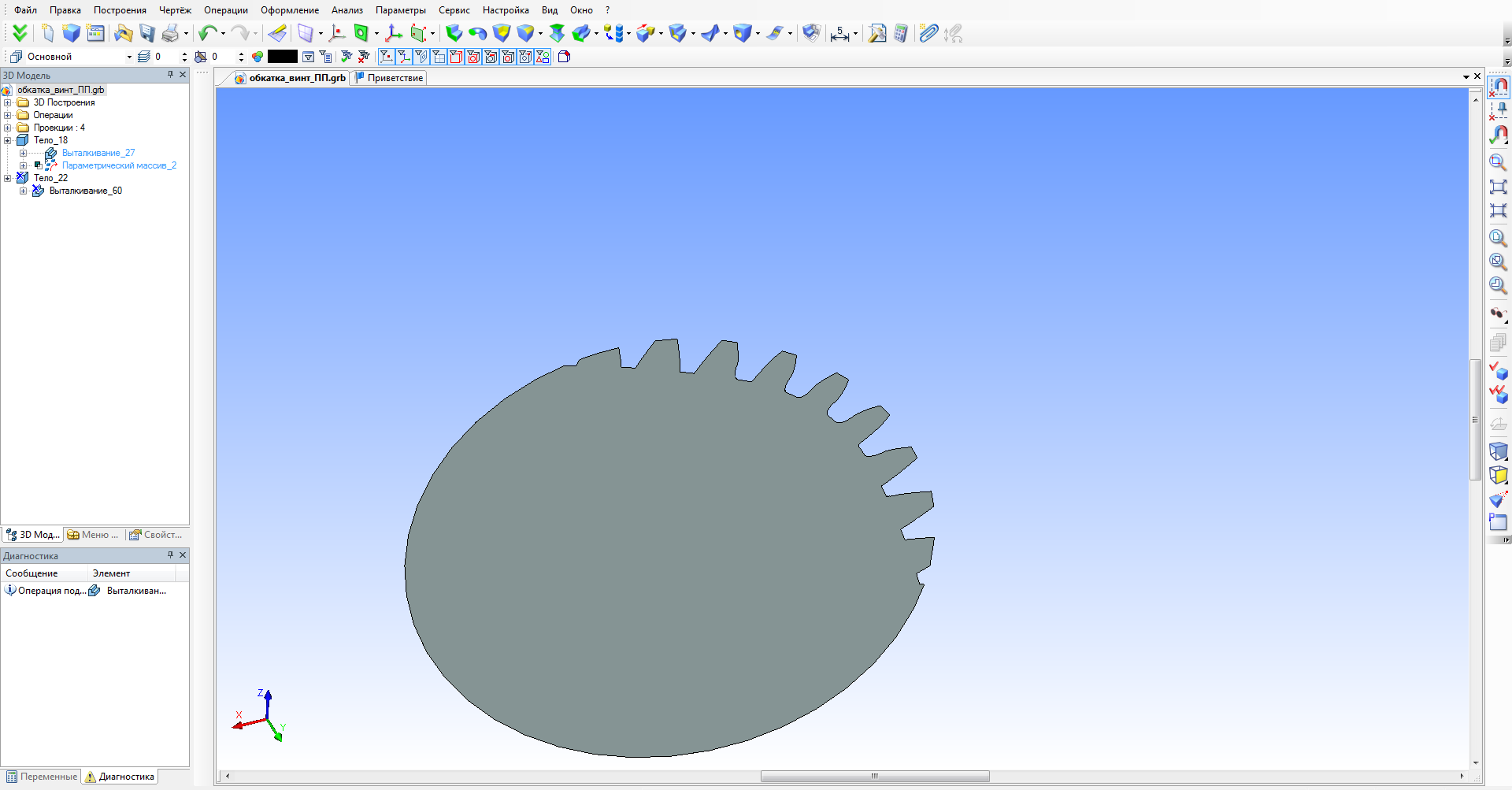
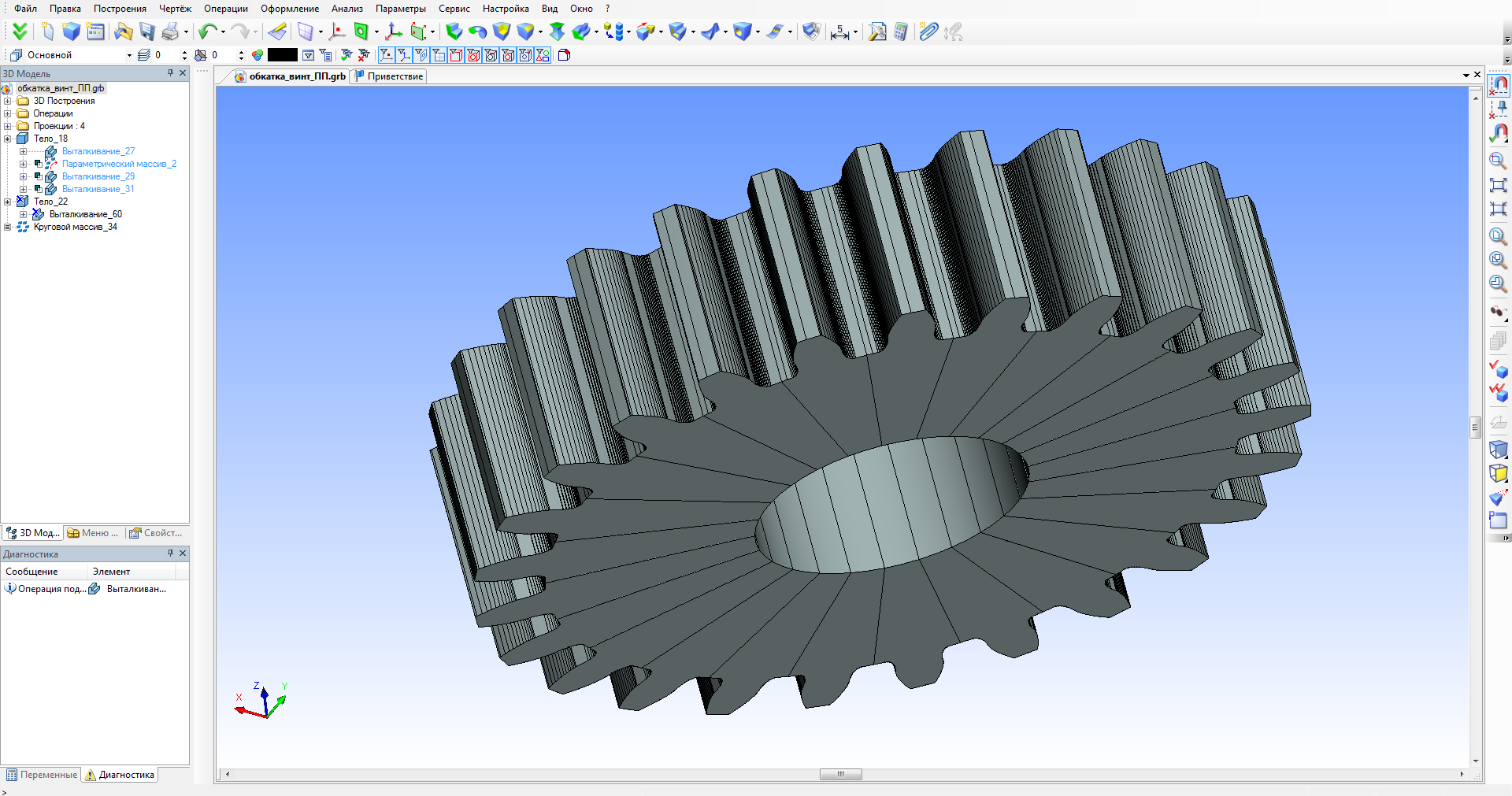
Затем, по рассчитанным параметрам, строится профиль зубчатого колеса и его трехмерная модель. Вместе с этим, в системе инструмента реализуется тонкостенная заготовка, на которой и будет определяться профиль обкаточного резца (рис. 4).

Рисунок 4 – Определение профиля зубчатого колеса внутреннего зацепления; построение трехмерной модели зубчатого колеса внутреннего зацепления

На следующем этапе профилирования необходимо определить движения инструмента и изделия и установить между ними связь. Обкаточный резец и зубчатое колесо с внутренними зубьями имеют вращательные движения, при этом вращаются они в одном направлении. А так как они находятся в зацеплении, то, как и у колес внутреннего зацепления, пара инструмент-деталь имеем передаточное отношение, которое определяется числами их зубьев z₀ и z₁ для обкаточного резца и зубчатого колеса соответственно. Тогда:

 _{u0 = z1 / z0} .                              (1)

Таки образом, можно определить условие обкатки:

  _{φ0 = φ1 / u0},                              (2)

где φ₀ – угол поворота обкаточного резца, φ₁ – угол поворота зубчатого колеса с внутренними зубьями.

Особенность данного метода профилирования заключается том, что инструмент “фиксируется”, а все движения передаются изделию с заданным профилем. То есть зубчатое колесо должно, кроме вращения во круг своей оси, вращаться вокруг оси инструмента. Для этого необходимо определить координаты оси инструмента в системе координат, жестко связанной с зубчатым колесом. Координаты определяются с помощью обратной результирующей матрицы MR, которая считается аналогично матрице прямого преобразования MS. 

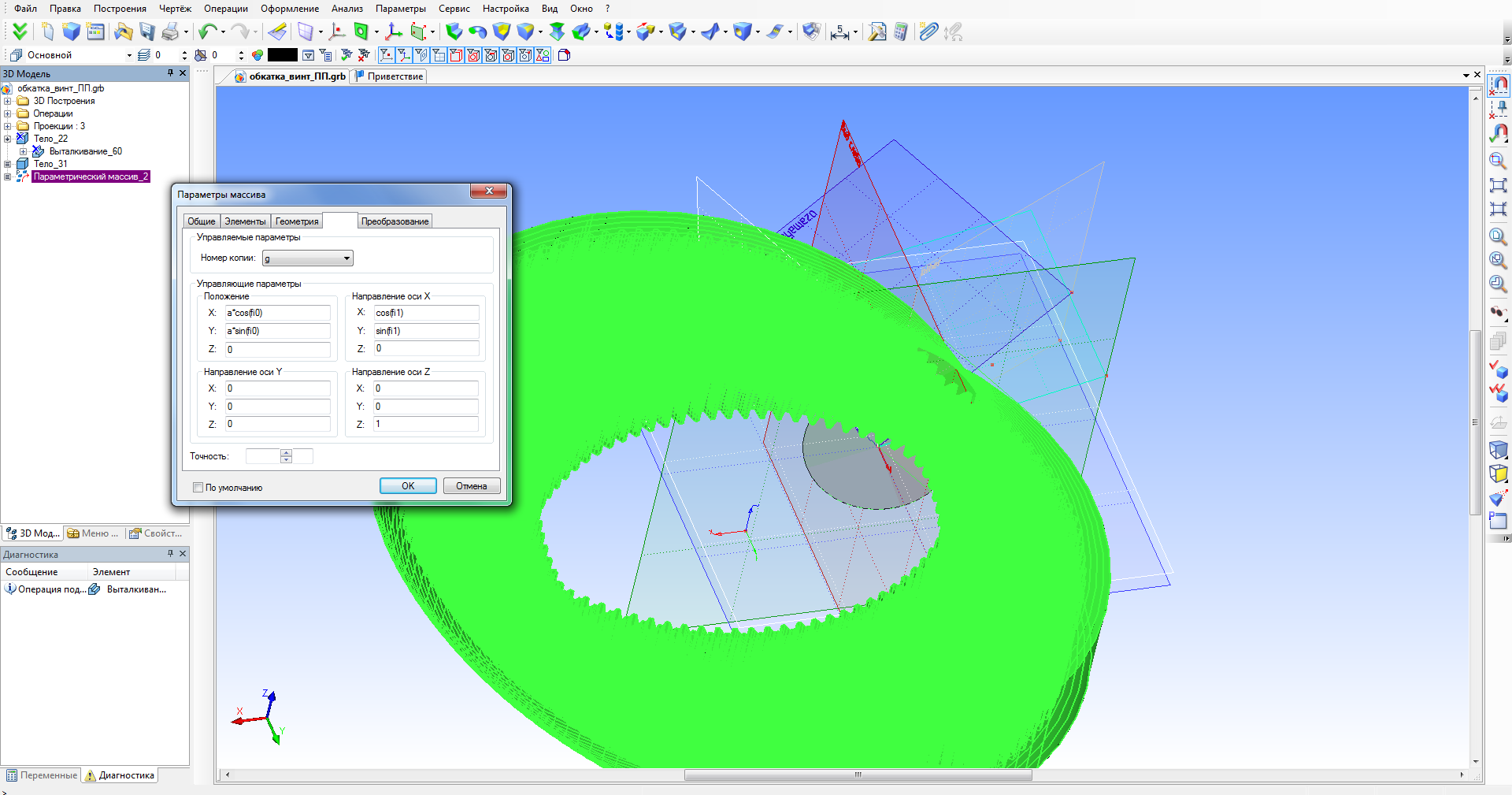
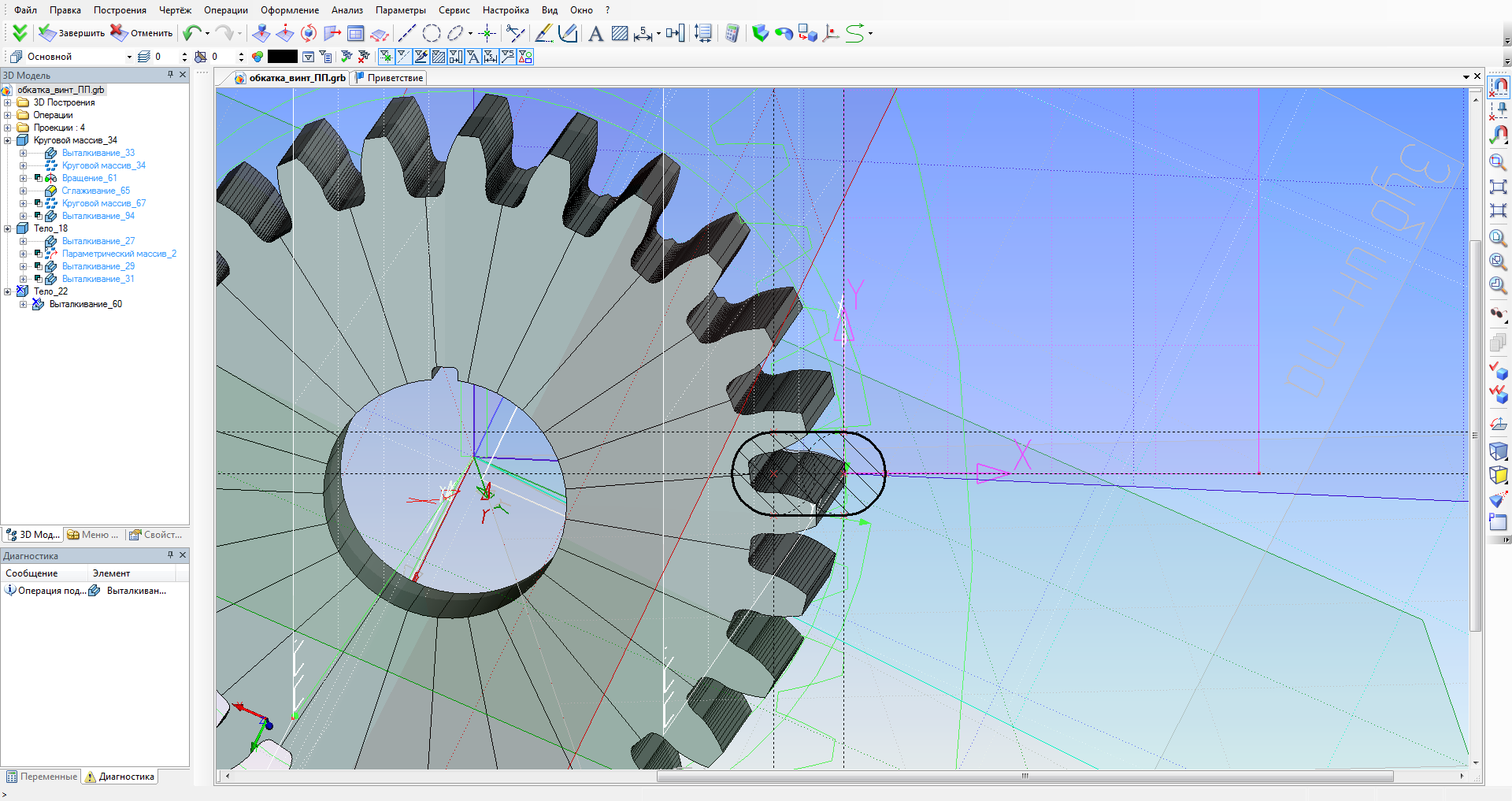
В среде t-Flex это реализуется за счет операции параметрический массив, где массив зубчатых колес совершает обкатку вокруг заготовки инструмента (рис. 5 и 6). 

Рисунок 5 – Параметры массива

Рисунок 6 – Результат операции “параметрический массив”

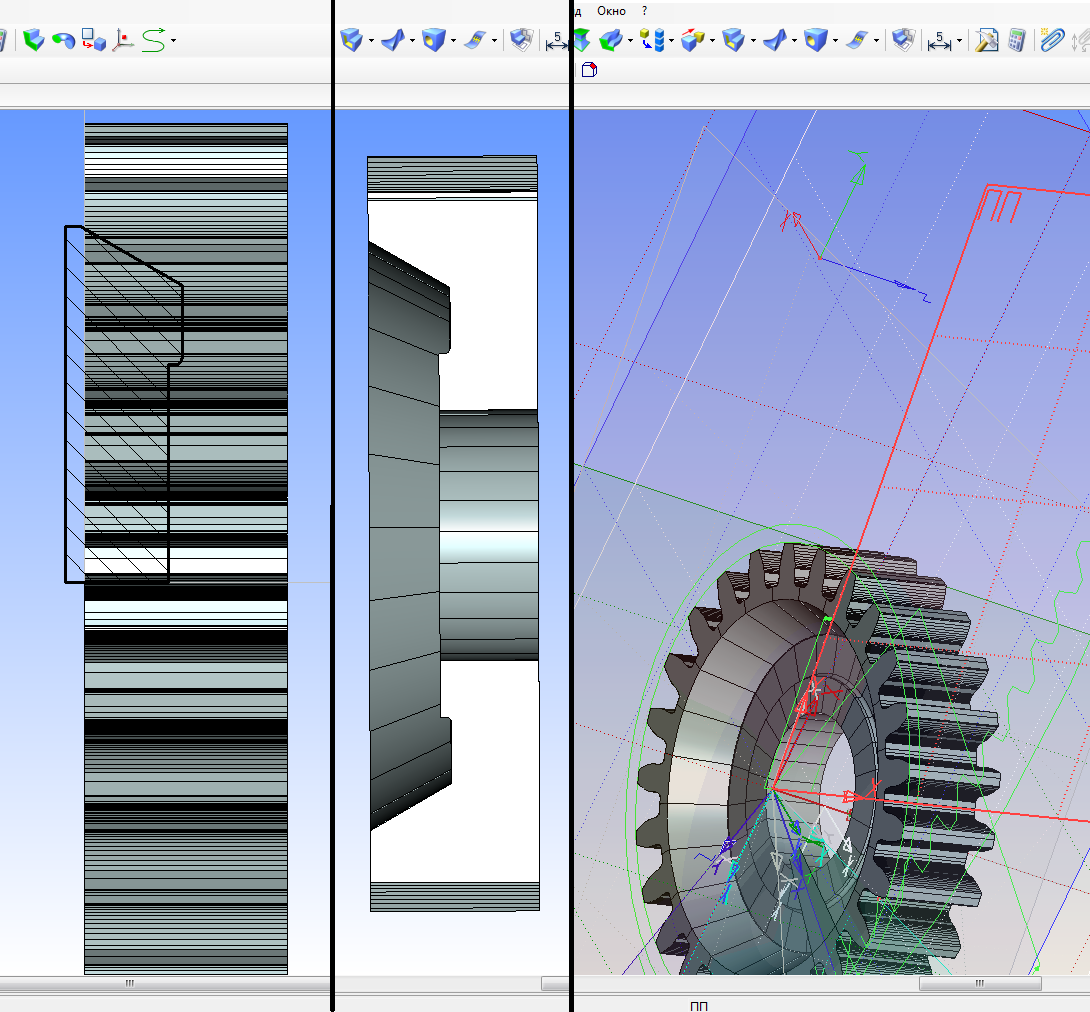
Следующим шагом необходимо из заготовки обкаточного резца вычисть булевой операцией результат параметрического массива (рис. 7).

Рисунок 7 – Результат булевой операции вычитания.

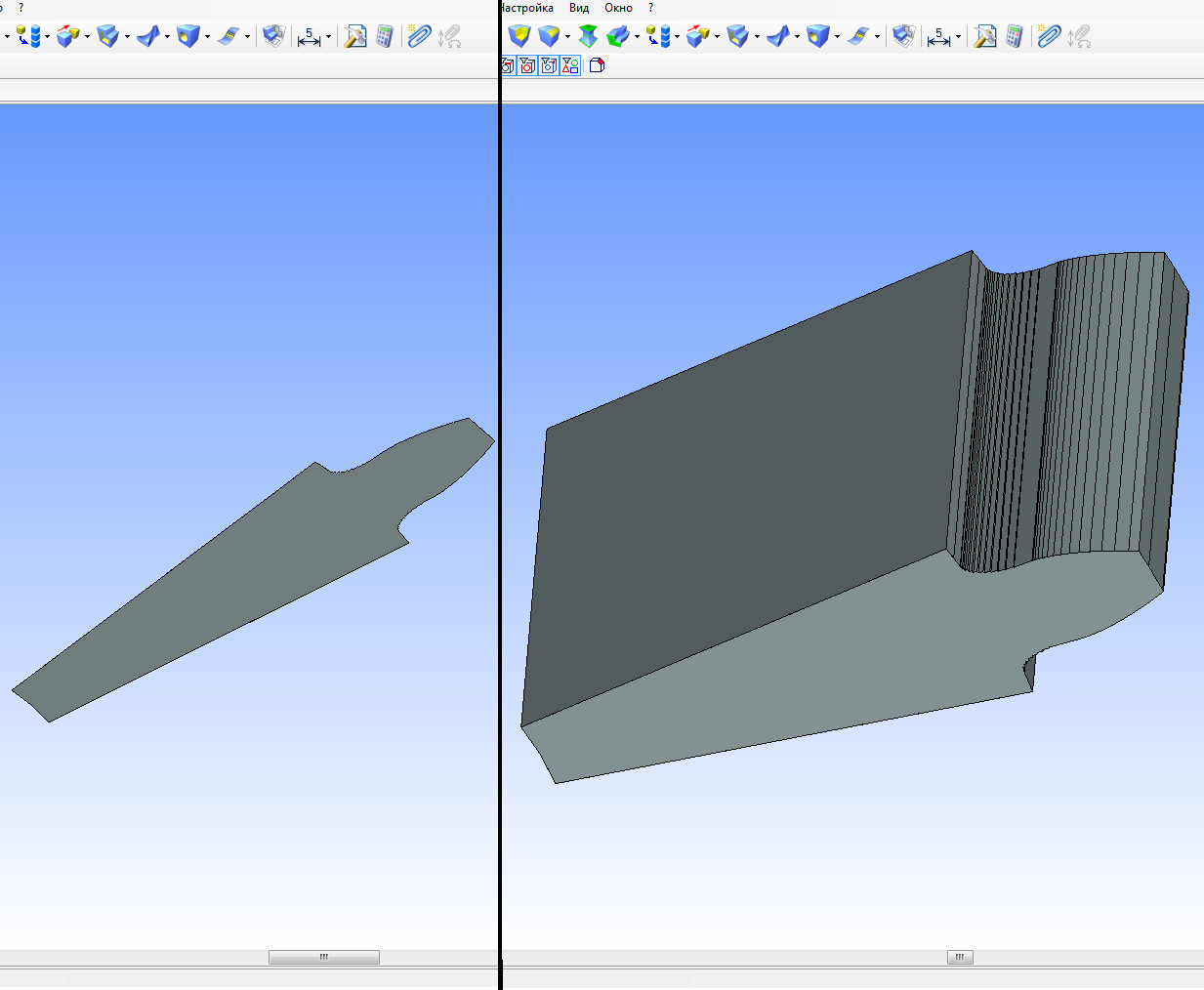
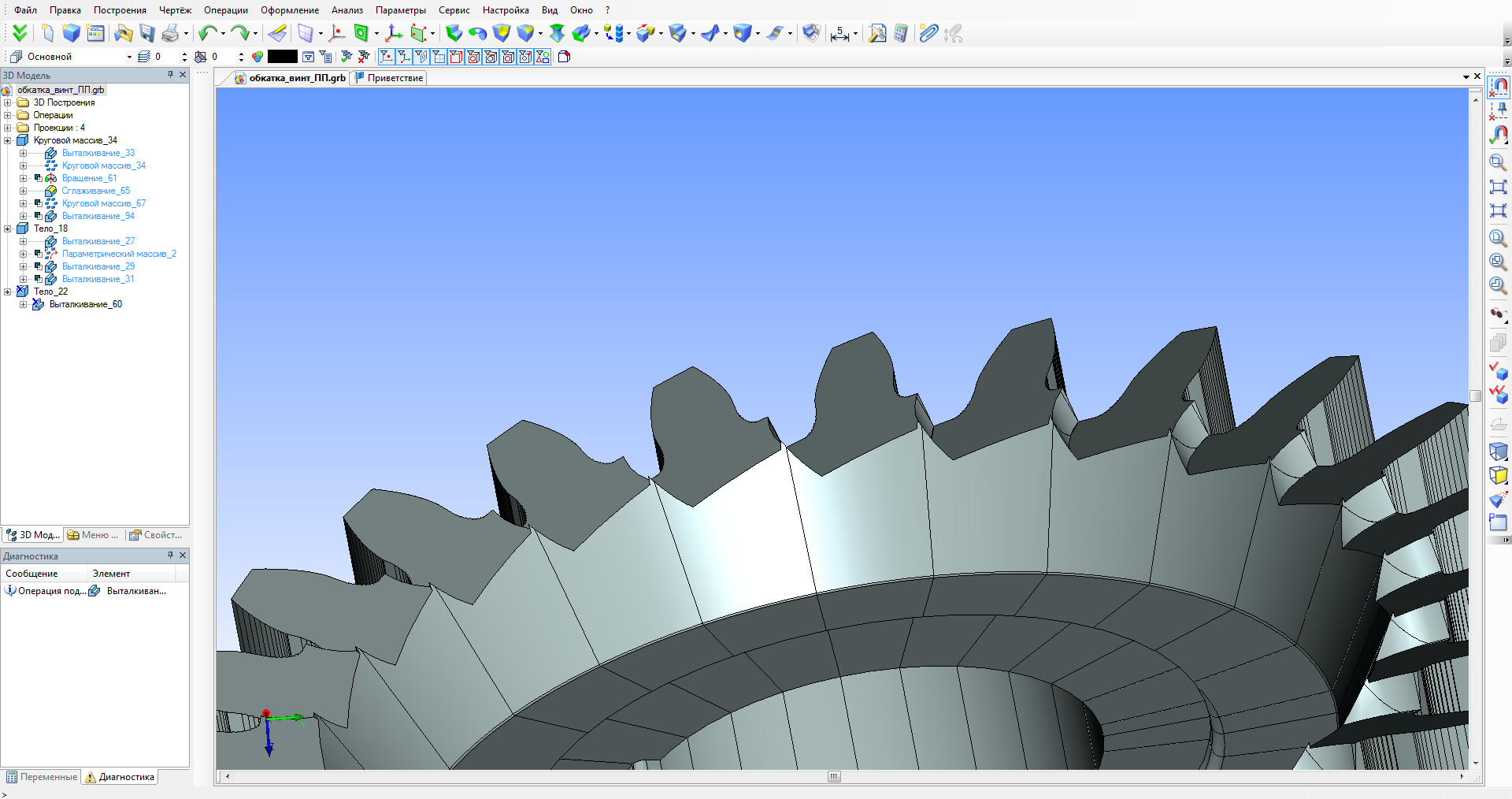
Для достижения результата поставленной задачи достаточно получить профиль на одном зубе инструмента (рис. 8), а далее массивом получить профиль всего обкаточного резца (рис. 9).

Рисунок 8 – Профиль одного зуба обкаточного резца

Рисунок 9 – Профиль всех зубьев обкаточного резца

Таким образом был получен профиль инструмента по заданному профилю зубчатого колеса. Для получения готовой модели инструмента необходимо сформировать опорный торец и выточку под переточку по передней поверхности (рис. 10), шпоночный паз и переднюю поверхность инструмента (рис. 11 и 12).

Рисунок 10 – Формирование опорного торца и выточки под переднюю поверхность

Рисунок 11 – Формирование передней поверхности; имитация обработки

Рисунок 12 – Результат формирования передней поверхности инструмента

В результате выполненной работы была получена трехмерная параметрическая модель обкаточного резца (рис. 13), которая наглядно демонстрирует применимость метода трехмерного моделирования для решения прямой задачи профилирования – определения профиля инструмента.

Рисунок 13 – Параметрическая модель обкаточного резца

 Модель применима для профилирования инструмента, ориентированного на обработку широкого спектра зубчатых колес внутреннего зацепления, с различными параметрами чисел зубьев, угла наклона зубьев, модуля и т.д. Также модель применима к зубчатым колесам не только эвольвентного профиля, но и других. Практическая ценность работы, заключается в решении задачи профилирования и определении эффективных путей улучшения выходных параметров инструмента.

1. Петухов, Ю.Е. Формообразование численными методами / Ю.Е. Петухов. – М. : «Янус-К», 2004. – 200 с.
2. Гречишников, В.А. Математическое моделирование в инструментальном производстве / В.А. Гречишников, Н.В. Колесов, Ю.Е. Петухов. – М. : МГТУ «СТАНКИН». УМО АМ, 2003. – 116 с.
3. Петухов, Ю.Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства : дис. … докт. техн. наук : 05.03.01 / Ю.Е. Петухов. – М., 2004. – 393 с.
4. Петухов, Ю.Е. Численные модели режущего инструмента для обработки сложных поверхностей / Ю.Е. Петухов, Н.В. Колесов // Вестник машиностроения. – 2003. – №5. – С. 61-63.
5. Петухов, Ю.Е. Профилирование режущих инструментов среде Т-flex CAD-3D / Ю.Е. Петухов // Вестник машиностроения. – 2003. – №8. – С. 67-70.
6. Петухов, Ю.Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Ю.Е. Петухов, П.В. Домнин // Вестник МГТУ «СТАНКИН». – 2011. – №3. – С. 102-106.
7. Колесов, Н.В. Система контроля сложных кромок режущих инструментов / Н.В. Колесов, Ю.Е. Петухов // ИТО: Инструмент. Технология. Оборудование. – 2003. – №2. – С. 42-45.
8. Петухов, Ю.Е. Компьютерная модель формообразования сложной поверхности / Ю.Е. Петухов, П.В. Домнин // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т. : сб. науч. ст. – Тула, 2010. – Т. 1. – С. 197-200.
9. Колесов, Н.В. Компьютерная модель дисковых фасонных затылованных фрез / Н.В. Колесов, Ю.Е. Петухов, А.В. Баринов // Вестник машиностроения. – 1999. – №6. – С. 57-61.
10. Домнин, П.В. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений / П.В. Домнин, Ю.Е. Петухов // Справочник. Инженерный журнал с приложением. – 2011. – №11. – С. 26-29.
11. Колесов, Н.В. Математическая модель червячной фрезы с протуберанцем / Н.В. Колесов, Ю.Е. Петухов // СТИН. – 1995. – №6. – С. 26-29.
12. Колесов, Н.В. Два типа компьютерных моделей режущего инструмента / Н.В. Колесов, Ю.Е. Петухов // СТИН. – 2007. – №8. – С. 23-26.
13. Петухов, Ю.Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю.Е. Петухов, П.В. Домнин // СТИН. – 2011 – №7. – С. 14-17.
14. Петухов, Ю.Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2012. – №3. – С. 28-32.
15. Петухов, Ю.Е. Некоторые направления развития САПР режущего инструмента / Ю.Е. Петухов // СТИН. – 2003. – №8. – С. 26-30.
16. Петухов, Ю.Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2014. – №1 (28). – С. 39-43.
17. Petukhov, Y.E. Shaping precision in machining a screw surface / Y.E. Petukhov, P.V. Domnin // Russian Engineering Research. – 2011. – T. 31. – №10. – С. 1013-1015.
18. Kolesov, N.V. Computer models of cutting tools / N.V. Kolesov, Y.E. Petukhov // Russian Engineering Research. – 2007. – T. 27. – №11. – С. 812-814.
19. Petukhov, Y.E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y.E. Petukhov, A.V. Movsesyan // Russian Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.
20. Петухов Ю.Е. Cпособ шлифования фасонных валов. Патент на изобретение RUS 863310  04.05.1979
21. Цвис Ю.В. Профилирование режущего обкатного инструмента. М.: МАШГИЗ, 1961. – 156с.
22. Волков Н.Н. Исследование и разработка инструмента для нарезания цилиндрических зубчатых колес с внутренними зубьями по методу зуботочения.: Дис. канд. тех. наук. – М., 1981. – 222с.
23. Кирютин А.С. Математическая модель профилирования обкаточных резцов // Современные научные исследования и инновации. 2014. № 10 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/10/38627
24. ГОСТ 16532–70. Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет геометрии. – введ. 01.01.72. – СССР : Государственный комитет стандартов Совета Министров СССР, 1972. – 43с.

Все статьи автора «Кирютин Алексей Сергеевич»