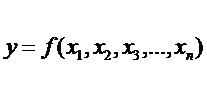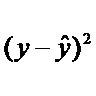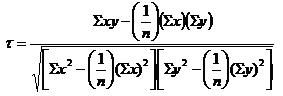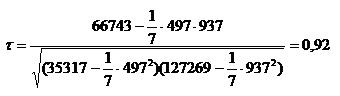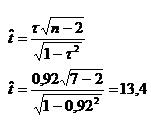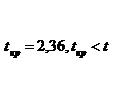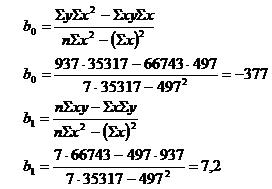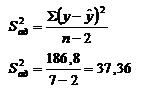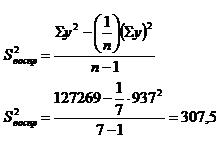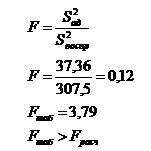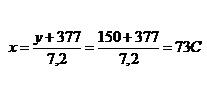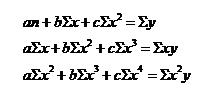Большинство научных исследований связано с экспериментом. Он может непосредственно проводиться на объекте или на его модели.

Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью [1…4].

При решении задачи используются математические модели объекта исследования, т.е. уравнение, связывающее параметр оптимизации с факторами. Это уравнение в общем виде выглядит следующим образом:

Для определения связи между двумя необходимыми параметрами можно воспользоваться парной регрессией. Парная регрессия представляет собой уравнение, описывающее связь между двумя переменными: зависимой переменной y и независимой переменной x.

Рассмотрим примеры использования линейной и нелинейной парной регрессии для определения зависимостей между оцениваемыми показателями при производстве сахара-песка [3, 4].

При производстве сахара используются диффузионные аппараты, которые имеют определенные недостатки, что не позволяет обеспечить оптимальные условия проведения процесса экстрагирования для получения максимального выхода сахара. Основными факторами [2], влияющими на ход процесса экстрагирования и полноту извлечения сахара из стружки, являются температурный режим, особенно в начальной стадии процесса, направление движения фаз, гидродинамика процесса, соотношение расхода масс экстрагента и стружки [5]. Таким образом, целесообразно определить зависимость выхода сахара (у, т/смену) от температуры в диффузионном аппарате (x, ^оС), что позволит найти оптимальный температурный режим для максимального выхода сахара. Исходные данные представлены в таблице 1.

Таблица 1 – Результаты эксперимента

№	x	y	x2	y2	xy
1	68	110	4624	12100	7480	112,6	-2,6	6,76
2	69	112	4761	12544	7728	119,8	-7,8	60,84
3	70	130	4900	16900	9100	127	3	9
4	71	135	5041	18225	9585	134,2	0,8	0,64
5	72	150	5184	22500	10800	141,4	8,6	73,96
6	73	150	5329	22500	10950	148,6	1,4	1,96
7	74	150	5476	22500	11100	155,8	-5,8	33,64
∑	497	937	35317	127269	66743			186,8

Для установления связи между изучаемыми переменными рассчитаем коэффициент парной корреляции:

Коэффициент корреляции – это статистический показатель зависимости двух случайных величин. Коэффициент корреляции может принимать значения от -1 до +1. При этом значение -1 будет говорить об отсутствии корреляции между величинами, 0 – о нулевой корреляции, а +1 – о полной корреляции величин. Т.е., чем ближе значение коэффициента корреляции к +1, тем сильнее связь между двумя случайными величинами.

Проведем оценку значимости коэффициента парной корреляции с помощью критерия Стьюдента.

Сравним полученное значение с критическим значением t-критерия, который определяется по таблице распределения Стьюдента:

Таким образом, коэффициент корреляции значим.

Найдем выборочные коэффициенты регрессии по следующей формуле:

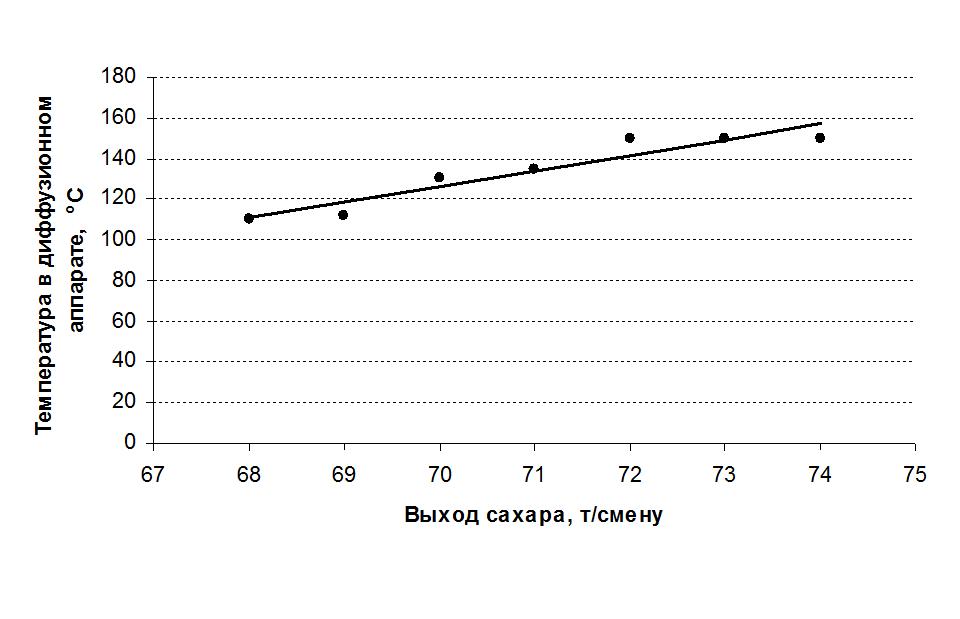
Уравнение регрессии имеет следующий вид (рис 1):

y=-377+7,2x

Рисунок 1 – Зависимость выхода сахара от температуры в диффузионном аппарате

 С помощью коэффициентов можно выяснить силу влияния факторов. Чем больше величина коэффициента, тем большее влияние оказывает фактор. В данном случае коэффициент имеет знак плюс. Это означает, что с увеличением значения фактора значение параметра оптимизации увеличивается.

Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным.

Значение дисперсии адекватности модели можно вычислить по следующей формуле:

Далее найдем дисперсию воспроизводимости :

Для того, чтобы проверить гипотезу об адекватности модели можно воспользоваться критерием Фишера:

На основании полученных данных можно сделать вывод, что модель адекватна.

Для выполнения нормы – 150 т/смену – температура в диффузионном аппарате должна достигать 73°С:

На практике для получения 150 т сахара в смену температура в аппарате должна быть в пределах 72–74°С.

В том случае, если предполагаемый характер процесса носит нелинейный характер, имеет смысл получить квадратичную зависимость.

Проведем анализ того же процесса в вакуум-аппарате. Принцип действия данного оборудования и диффузионного аппарата похожи, так как они направлены на одну цель – достичь наибольшего выхода сахара-песка.

В качестве переменных примем:

x – температура в вакуум – аппарате, ^оС;

y – выход сахара, т/смену.

Исходные данные представлены в таблице 2.

Таблица 2 – Результаты эксперимента

Составим и решим систему уравнений:

5a+330b+33630c=685

330a+33630b+2759300c=56245

33630a+2759300b+226464354c=3667035

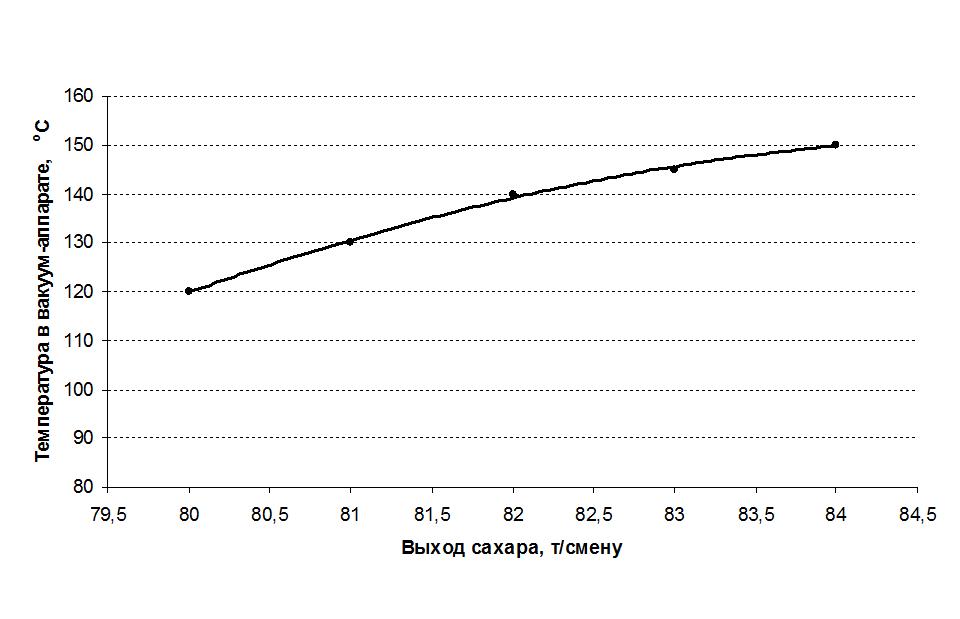
Уравнение регрессии будет иметь следующий вид (рис. 2), модель адекватна:

y=-145-9,07x+0,06x²

Рисунок 2 – Зависимость выхода сахара от температуры в вакуум-аппарате

Таким образом, на основании статистических данных, полученных при анализе деятельности предприятия, были получены зависимости между технологическими режимами работы оборудования и конечным выходом сахара-песка. На основании полученных данных можно сделать вывод, что на ОАО «Атмис-сахар» правильно подобран температурный режим. Выход сахара соответствует нормативным показателям.

1. Адлер Ю.П. Введение в планирование эксперимента [Текст] / Ю.П. Адлер.- М.: Металлургия, 1968. - 155 с.
2. Тарасов, Р.В. Выбор параметра оптимизации и факторов в рамках подготовки к активному эксперименту [Текст] /  Р.В. Тарасов, Л.В. Макарова, О.Ф. Акжигитова // Современные научные исследования и инновации. – Апрель 2014. - № 4 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33940
3. Регрессионный анализ. Линейная регрессия, [Электронный ресурс]. Режим доступа: http://kurs.ido.tpu.ru/courses/econometrica/tema5.htm
4. Нелинейная регрессия, [Электронный ресурс]. Режим доступа: http://kurs.ido.tpu.ru/courses/econometrica/tema9.htm
5. ГОСТ 21-94. Сахар-песок. Технические условия [Текст]. – Взамен ГОСТ 21-78. - М.: Издательство стандартов, 1997. – 14 с.

Все статьи автора «Макарова Людмила Викторовна»