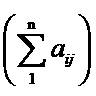На стадии создания и проектирования продукции, в том числе и строительного назначения, необходимо проведение значительного количества исследований, в том числе и экспериментального плана. Эффективным инструментом решения задач оптимизации, например, при регулировании структуры и свойств строительных композиционных материалов, является планирование эксперимента.
Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью [1]. При этом существенно следующее:
- стремление к минимизации общего числа опытов;
- одновременное варьирование всеми переменными, определяющими процесс, по специальным алгоритмам;
- использование математического аппарата, формализующего многие действия экспериментатора;
- выбор четкой стратегии, позволяющей получать адекватные данные и принимать обоснованные решения после каждой серии экспериментов.
При использовании статистического подхода к планированию экспериментов рекомендуется следующая схема [2, 3]:
- Признание факта существования задачи и ее формулировка.
- Выбор факторов и уровней.
- Выбор переменной отклика (параметра оптимизации).
- Выбор плана эксперимента.
- Проведение эксперимента.
- Анализ данных.
- Выводы и рекомендации.
Эффективность решения конкретной задачи планирования эксперимента в значительной степени зависит от четкого понимания изучаемой проблемы, формулировки целей и задач исследования, а также эффективного выбора параметра оптимизации и факторов.
На начальном этапе исследований большое внимание следует уделять сбору априорной информации, основанной как на анализе научно-технических источников, так и на основе собственных, заранее проведенных экспериментальных исследований.
При выборе параметра оптимизации экспериментатор должен быть уверен, что отклик (параметр оптимизации), действительно содержит информацию об исследуемом объекте. При этом должен выполняться ряд требований, а именно [1]:
- Параметр оптимизации должен быть количественным.
- Параметр оптимизации должен выражаться одним числом.
- Однозначность в статистическом смысле.
- Эффективность оценивания системы.
- Эффективность параметра оптимизации в статистическом смысле.
- Универсальность (полнота).
- Параметр оптимизации должен иметь физический смысл, быть простым и легко вычисляемым.
Также при формировании списка откликов необходимо знать размерность откликов, область их определения и необходимую точность фиксирования результатов.
При планировании эксперимента необходим учет всех факторов, которые могут влиять на изучаемый объект (или процесс). Так же, как и параметр оптимизации, каждый фактор имеет область определения (варьируется на разных уровнях) при соблюдении следующих требований [1]:
- Факторы должны быть управляемыми.
- Фактор должен быть операциональным.
- Точность замера факторов должна быть возможно более высокой.
- Факторы должны быть однозначны.
- Совместимость факторов.
- Независимость факторов.
В то же время, известно [1], что число факторов определяет количество опытов многофакторного эксперимента и увеличение числа факторов, включаемых в исследование, приводит к значительному увеличению объема экспериментальной работы.
При установлении зависимости параметров процесса от факторов для сокращения объема экспериментальной работы желательно иметь по возможности меньшее число таких исследуемых факторов. Однако следует иметь в виду, что эксперименты, направленные на отыскание оптимальных условий протекания процесса, могут потерять всякий смысл при исключении из числа факторов хотя бы одного фактора, оказывающего существенное влияние на параметр оптимизации.
В связи с этим, актуальной становится задача снижения количества рассматриваемых факторов и включения в активных эксперимент наиболее значимых из них.
Для решения такого рода задач, связанных со снижением многообразия рассматриваемых факторов, эффективно используются методы, основанные на экспертной оценке, например, метод априорного ранжирования факторов [3…5].
Рассмотрим процедуру подготовки к эксперименту на примере оптимизации эксплуатационных характеристик керамического кирпича.
Керамический кирпич применяется для кладки и облицовки несущих и самонесущих стен и других элементов зданий и сооружений и характеризуется следующими основными показателями качества: прочность при сжатии, прочность при изгибе, средняя плотность, пустотность, водопоглощение, морозостойкость и т.д.
Одним из важнейших свойств керамического кирпича является его средняя плотность. В конечном итоге этим свойством определяются теплоизоляционные свойства кирпича и кирпичной кладки.
Среди всего множества факторов, оказывающих влияние на плотность керамического кирпича, можно выделить две группы: рецептурные факторы и технологические факторы. С учетом того, что процесс производства керамического кирпича достаточно сложен, особое внимание при производстве кирпича следует уделить вопросам оптимизации технологических процессов.
Рассмотрим следующие факторы:
- время вылеживания глины (X1);
-зазор между валками по выступам и по впадинам вальцов грубого помола (X2);
- зазор между валками вальцов тонкого помола (X3);
- частота вращения валков лопастного смесителя (X4);
- величина разряжения в вакуум-камере (X5);
- время нахождения кирпича-сырца в туннельной сушилке (X6);
- циркуляция воздуха в туннельной сушилке (X7);
- температура теплового агента туннельной сушилки (X8);
- температура обжига (X9);
- разряжение в печи обжига (X10);
- продолжительность обжига (X11).
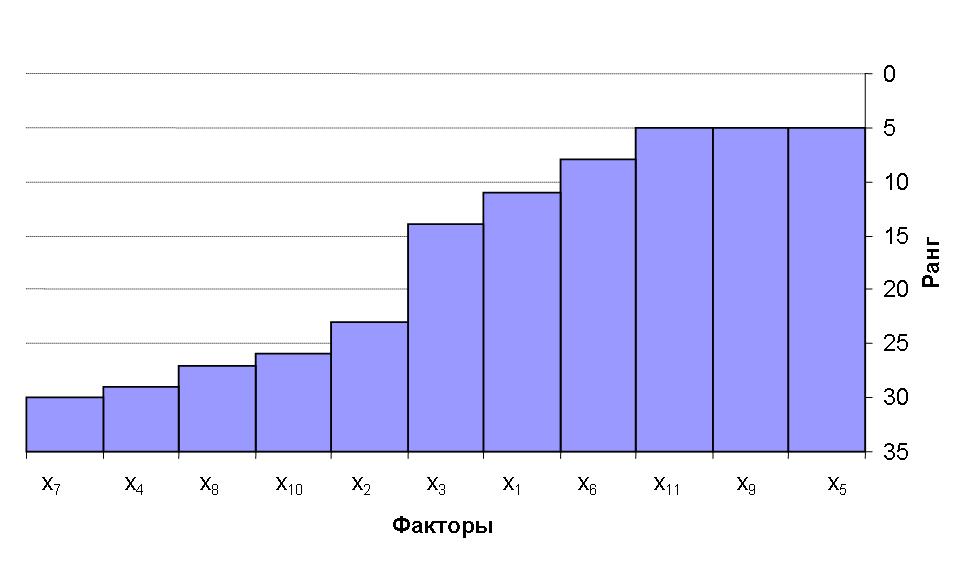
Для выбора наиболее значимых факторов воспользуемся методом априорного ранжирования [3…5]. Результаты опроса экспертов и результаты расчета представлены в табл. 1 и на рис. 1. Расчетное значение коэффициента конкордации ω=0,65.
Таблица 1 – Результаты опроса экспертов
|
Исследователи (m) |
Показатели качества (n=11) |
|||||||||||
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9
|
X10
|
X11
|
||
|
1 |
3 |
7 |
4 |
8 |
2 |
2 |
7 |
6 |
1 |
5 |
2 |
30 |
|
2 |
2 |
5 |
4 |
6 |
1 |
2 |
7 |
8 |
1 |
8 |
1 |
54 |
|
3 |
4 |
6 |
3 |
7 |
1 |
2 |
8 |
6 |
2 |
6 |
1 |
36 |
|
4 |
2 |
5 |
3 |
8 |
1 |
2 |
8 |
7 |
1 |
7 |
1 |
42 |
|
11 |
23 |
14 |
29 |
5 |
8 |
30 |
27 |
5 |
26 |
5 |
||
|
Δi |
-7 |
5 |
-4 |
11 |
-13 |
-10 |
12 |
9 |
-13 |
8 |
-13 |
|
|
(Δi)2 |
49 |
25 |
16 |
121 |
169 |
100 |
144 |
81 |
169 |
64 |
169 |
S=1107 |
Рис. 2. Средняя априорная диаграмма
По результатам проведенного психологического эксперимента было отобрано для дальнейших исследований три фактора – X5 , X9 , X11, принимаемых в качестве основных и занимающие по диаграмме первые три места. Уровни факторов и интервалы варьирования представлены в табл. 2.
После выбора факторов можно построить матрицу планирования, которая представляет собой матрицу планирования, где строки соответствуют различным опытам, а столбцы – значениям факторов (табл. 3).
Таблица 2 – Уровни факторов
|
Кодированные значения |
Факторы |
|||
|
X5, МПа |
X9, °С |
X11, час |
||
|
Верхний уровень |
+1 |
9,8 |
1000 |
52 |
|
Нижний уровень |
-1 |
8 |
800 |
48 |
|
Основной уровень |
0 |
8,9 |
900 |
50 |
|
Интервал варьирования |
Δ |
0,9 |
100 |
2 |
Таблица 3 – Матрица планирования
|
№ опыта |
X5 |
X9 |
X11 |
Y |
|||
|
Кодир. знач. |
Натур. знач. |
Кодир. знач. |
Натур. знач. |
Кодир. знач. |
Натур. знач. |
||
|
1 |
+ |
9,8 |
+ |
1000 |
+ |
52 |
|
|
2 |
- |
8 |
+ |
1000 |
+ |
52 |
|
|
3 |
+ |
9,8 |
- |
800 |
+ |
52 |
|
|
4 |
- |
8 |
- |
800 |
+ |
52 |
|
|
5 |
+ |
9,8 |
+ |
1000 |
- |
48 |
|
|
6 |
- |
8 |
+ |
1000 |
- |
48 |
|
|
7 |
+ |
9,8 |
- |
800 |
- |
48 |
|
|
8 |
- |
8 |
- |
800 |
- |
48 |
|
Количество параллельных опытов одинаково.
Чтобы исключить влияние систематических ошибок, вызванных внешними условиями, рекомендуется случайная последовательность при постановке опытов. Эта задача может быть решена путём придания последовательности опытов случайного характера. Для этого можно воспользоваться таблицей случайных чисел.
Исходя из того, что имеет место два параллельных опыта, всего необходимо провести 16 измерений. Из таблицы случайных чисел получим следующую последовательность: 1; 8; 3; 2; 7; 9; 5; 6; 14; 15; 4; 11; 10; 12; 16.
Библиографический список
- Адлер, Ю.П. Введение в планирование эксперимента [Текст] / Ю.П. Адлер.- М.: Металлургия, 1968. – 155 с.
- Монтгомери, Д.К. Планирование эксперимента и анализ данных [Текст] / Д.К. Монтгомери.– Л.: Судостроение, 1980. – 384 с.
- Тарасов, Р.В. Оценка значимости факторов методом априорного ранжирования [Текст] / Р.В. Тарасов, Л.В. Макарова, К.М. Бахтулова // Современные научные исследования и инновации. – Апрель 2014. – № 4 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33181 (дата обращения: 03.04.2014).
- Тарасов, Р.В. К вопросу применения экспертных методов в прогнозировании процессов, оценке уровня качества и принятии управленческих решений [Текст] / Р.В. Тарасов, Л.В. Макарова, О.Ф. Акжигитова // Современные научные исследования и инновации. – Апрель 2014. – № 4 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33142 (дата обращения: 02.04.2014).
- Макарова, Л.В. Экспертные методы в управлении качеством [Текст] /Л.В. Макарова, Р.В. Тарасов.- Учебное пособие.- Пенза: ПГУАС, 2012.-92с.
Количество просмотров публикации: Please wait