Электродвигатели – доминирующий класс потребителей электроэнергии в мире. Во многих применениях электродвигатель большую часть времени работает с нагрузкой, меньшей номинальной. При этом КПД двигателя оказывается существенно ниже, чем при номинальном моменте на валу [1]. Специальные стратегии скалярного и векторного управления позволяют достичь оптимума энергопотребления в различных условиях нагрузки электродвигателя. Обзор состояния зарубежных работ, посвященных этой проблеме, можно найти в [2-4]. Из последних отечественных публикаций можно привести исследования [5-7].

В настоящем статье обсуждается вопрос минимизации энергопотребления для двигателя, работающего в установившемся режиме с постоянным моментом нагрузки. Описываемый далее алгоритм относится к методам на основе модели мощности потерь. Вычисленная уставка тока намагничивания минимизирует установившуюся мощность потерь в обмотках без учета мощности в потерь в сердечнике.

Главное отличие описанного метода от других ранее опубликованных состоит в параметрической идентификации модели потерь за счет накопления данных о найденных ранее оптимумах энергопотребления. Таким образом, реализованный метод представляет собой гибридный алгоритм, основанный на поисковой оптимизации, которая заменяется после идентификации модели на прямое вычисление уставки тока намагничивания.

В этой главе мы не детализируем алгоритм до степени, достаточной для его прямой реализации. Вместо этого приводится описание концепта и его проверка на корректность по снятым с электродвигателей экспериментальным данным.

1. Предварительные сведения

1.1 Модель электродвигателя

Рассмотрим модель двигателя на основе обратной Г-образной схемы замещения [8] с ориентацией оси d вращающейся системы координат параллельно потокосцеплению ротора . В пространстве состояний, данная модель реализуется системой дифференциальных уравнения четвертого порядка:

где – синхронная скорость, – скорость вращения вала двигателя (электрическая – т.е. механическая , умноженная на число пар полюсов p), – электромагнитный момент вращения, развиваемый двигателем. Параметры статора двигателя: , параметры ротора двигателя .

Все напряжения и токи в модели являются действующими значениями и полученными с помощью преобразований Кларка и Парка, инвариантных по мощности.

1.2 Модель потерь в обмотках при магнитном насыщении

Насыщение индуктивностей в асинхронных электродвигателях – неотъемлемая черта их функционирования даже для токов статора, заметно меньших номинальных значений. Модель потерь [7] в установившемся режиме как функция от тока намагничивания

(*)

оказывается недостаточно точной, поскольку при насыщении индуктивности намагничивания двигателя, значение перестает быть постоянным и является функцией от тока .

С учетом насыщения индуктивности намагничивания, квадратурный ток в устанавливавшемся режиме записывается в виде:

тогда мощность потерь выражается как

Характеристика может быть получена в результате следующей экспериментальной процедуры. Вал двигателя связывается с нагрузочной машиной, обеспечивающей известный постоянный момент . При ступенчатом варьировании тока намагничивания измеряется установившееся значение квадратурного тока как зависимость от . В результате, искомая характеристика может быть вычислена как . Очевидно, что подобная процедура может быть выполнена только в лабораторных условиях, что значительно затрудняет применимость методов на основе модели потерь к произвольному двигателю.

2. Метод минимизации энергопотребления

2.1 Условие оптимальности

Дифференцирование по дает

Обозначив и приравняв , находим условие минимума энергопотребления

(1)

При отсутствии насыщения это условие интерпретируется как равенство мощностей потерь по оси d и по оси q .

Разрешение уравнения (1) по для получения минимизирующей уставки тока – есть основа предлагаемого метода. Однако, для решения должна быть известна характеристика .

2.2 Идентификация характеристики намагничивания

Предположим, что найдено оптимальное значение тока намагничивания . Это может быть сделано, например, в результате применения методов поисковой оптимизации, описанных в предыдущей главе. Тогда условие (1) выполняется для значения . Решая (1) как уравнение относительно x, получаем

. (2)

где и – значения токов при минимальном .

Если электродвигатель работает с различными механическими нагрузками (или, эквивалентно, обеспечивается движение с различными постоянными ускорениями), то определение оптимума в каждом случае дает свое значение x. В результате, имеем вектор собранных ранее значений оптимального тока намагничивания и соответствующих им значений характеристики x: , таких что .

Анализ экспериментальных данных показывает, что зависимость может быть аппроксимирована линейно. Таким образом, возникает задача линейной регрессии по экспериментальным данным и X для получения коэффициентов линейной аппроксимации:

(3)

Для ее решения предлагается использование рекурсивного алгоритма наименьших квадратов [9], который позволяет осуществить вычисление коэффициентов b без хранения векторов и X. Рекурсивное обновление вектора коэффициентов b осуществляется по следующим соотношениям:

(4)

где – ковариационная матрица размерностью , изначально заполненная достаточно большими числами (близкими к машинной бесконечности), .

Каждый раз после того как найден новый оптимум потерь согласно (*), происходит обновление вектора коэффициентов b согласно правилу рекурсивного алгоритма наименьших квадратов (4).

2.3 Алгоритм

Полный алгоритм минимизации энергопотребления не приводится, далее рассматриваются только его основные составляющие.

Начальными условиями являются . Если обнаружено, что момент двигателя изменился и токи статора установились и постоянны в течение некоторого времени, то инициируется численный поиск оптимального значения уставки тока намагничивания . В качестве начального значения используется решение (1) относительно , в котором характеристика согласно линейной аппроксимации (3). После того, как найдено , вычисляется значение x согласно (2) и коэффициенты линейной аппроксимации обновляются по правилу (4). Исключение поискового алгоритма возможно после некоторого момента, когда постоянно обнаруживается, что найденный оптимум совпадает с начальным значением, вычисляемым по (1). На всех этапах алгоритма необходимо контролировать, чтобы уставка тока намагничивания не превышала номинальные значения.

3. Экспериментальная проверка

Для проверки работоспособности были проделаны эксперименты с двумя электродвигателями: номинальной мощностью 4 кВт (DRS112M4) и 0.37 кВт (DRS71S4). Суть экспериментов сводилась к следующему: электродвигатель, связанный с управляемой нагрузочной машиной, был запитан от векторного частотного преобразователя, при этом изменялась уставка тока намагничивания и вычислялась мощность потерь в обмотках согласно (*). Эксперимент повторялся для разных значений нагрузки на валу . В результате получилось семейство характеристик мощности потерь для разных моментов нагрузки на валу.

Измеренные данные обрабатывались следующим образом. По характеристике , снятой для конкретного момента нагрузки , определялось значение тока намагничивания , минимизирующее мощность потерь и рассчитывалась величина x согласно (2). По собранным значениями и x для различных моментов на валу проводилась линейная регрессия для получения коэффициентов аппроксимации (3).

С использованием аппроксимированной зависимости согласно (2) были вычислены оптимальные значения , удовлетворяющие (1). Результаты были нанесены на экспериментально полученные графики для того, чтобы убедиться в соответствии вычисленным и действительным минимумам мощности потерь. Соответствующие зависимости приведены на рисунках 1-4.

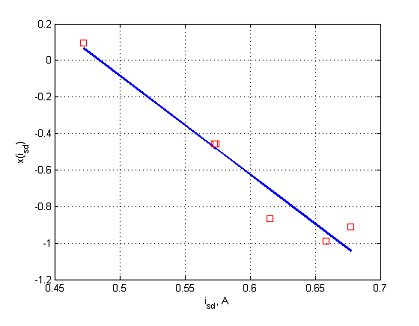
Рисунок 1. Зависимость для двигателя 0.37 кВт: экспериментальные точки (обозначены квадратными маркерами) и линейная аппроксимация.

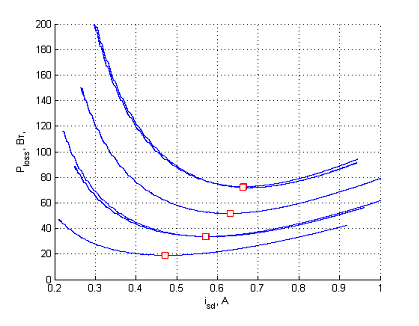
Рисунок 2. Зависимости для двигателя 0.37 кВт, квадратными точками обозначены вычисленные минимумы согласно (1).

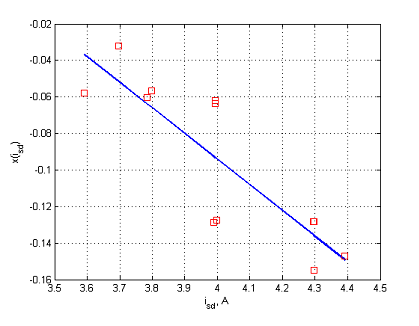
Рисунок 3. Зависимость для двигателя 4 кВт: экспериментальные точки (обозначены квадратными маркерами) и линейная аппроксимация.

Рисунок 4. Зависимости для двигателя 4 кВт, квадратными точками обозначены вычисленные минимумы согласно (1).

Из представленных на рисунках 2 и 4 графиков видно, что теоретически вычисленные минимумы согласно условию (1) и линейной аппроксимации с практической точки зрения хорошо согласуются с действительными минимумами мощности потерь двигателя.

Заключение

В настоящем разделе был рассмотрен вариант метода минимизации мощности потерь в обмотках двигателя, который использует информацию о найденных ранее минимумах потерь для идентификации характеристики насыщения индуктивности намагничивания двигателя. Алгоритм не требует предварительного измерения зависимости индуктивностей от тока намагничивания и может применяться при работе электродвигателя в составе оборудования. Метод использует на своем начальном этапе работы алгоритм прямого численного поиска минимума мощности потерь, и таким образом относится к гибридным алгоритмам. По мере накопления информации о характеристике насыщения двигателя, численный поиск исключается как избыточный этап.

1. Панкратов В.В., Зима Е.А. Энергооптимальное векторное управление асинхронными электроприводами: Учеб. пособие. – Новосибирск: Изд-во НГТУ, 2005. – 120 с.
2. Raj C. T., Srivastava S. P., Agarwal P. Energy efficient control of three-phase induction motor – a review // International Journal of Computer and Electrical Engineering. – 2009. – Т. 1. – №. 1. – С. 61-70.
3. Bazzi A. M., Krein P. T. Review of methods for real-time loss minimization in induction machines //Industry Applications, IEEE Transactions on. – 2010. – Т. 46. – №. 6. – С. 2319-2328.
4. Blanusa B. New Trends in Efficiency Optimization of Induction Motor Drives //New Trends in Technologies: Devices, Computer, Communication and Industrial Systems. Rijeka: Sciyo. – 2010.
5. Толочко О. И., Розкаряка П. И., Чекавский Г. С. Оптимизация энергопотребления позиционного электропривода с векторным управлением асинхронным двигателем // Сборник научных трудов ДонНТУ. Серия: «Элекротехника и энергетика». – Вып. – 2011. – Т. 11. – №. 186. – С. 396-400.
6. Семыкина И. Ю. (рук), Научно-технический отчет о выполнении 3 этапа Государственного контракта № 14.740.11.1105 от 24 мая 2011 г. «Разработка энергоэффективных средств управления электроприводами горных машин с учетом особенностей динамических режимов их работы в рамках создания энергосберегающих систем распределения и потребления электроэнергии» / Кемерово, 2011.
7. Борисевич А.В. Об одном подходе к оптимизации энергопотребления частотно-управляемого асинхронного электропривода // Материалы 2-й Международной научно-практической конференции Современное машиностроение. Наука и образование. – СПб.: Изд-во Политехн. ун-та, 2012. – С. 189-196.
8. Trzynadlowski A. M. Control of induction motors. – Academic Pr, 2001. – 228 p.
9. Ake Bjorck. Numerical Methods for Least Squares Problems, – SIAM-Mathematics, 1996, – 408 pp.

Все статьи автора «Борисевич Алексей Валерьевич»