Введение
В работах [1] и [2] представлены разработки Maple-процедур, позволяющих изучать распределение простых в пространстве одного и двух измерений. В настоящей статье тема будет продолжена. Речь пойдёт о двух наиболее обсуждаемых и отчасти родственных геометрических представлениях целочисленных последовательностей: скатерти Улама и спирали Сакса. Хотя обозреваемые геометрические структуры являются всего лишь формой, значимость подобных исследований состоит в том, что они должны способствовать поиску наиболее «простого», понятного и конструктивного распределения простых чисел.
1. Скатерть Улама
Один из наиболее компактных способов иллюстрации размещения простых чисел на плоскости был обнаружен в 1963 году Станиславом Уламом [3].
Улам размещал натуральные числа, начиная с некоторого данного, по спирали, вначале на бумажном листе в клетку, затем на экране компьютера по соответствующей программе. При этом положение простых чисел отмечалось особо. В результате получалось изображение, называемое теперь скатертью Улама.
Следующая процедура Ulam(s,z,ch) возвращает изображение скатерти Улама для s витков спирали.
> restart:
> with(plottools): with(plots):
> Ulam:=proc(s,z,ch)
local tt,t1,x,y,n,i,j,p,c,a,b:
tt:=NULL:t1:=NULL:
tt:=tt,[0,0]: t1:=[0,0,ch]:
x:=0: y:=0: n:=1:
for i from 1 to s*2 do
if i mod 2 = 1 then
for j to i do
n:=n+1:x:=x+1: tt:=tt,[x,y]: t1:=t1,[x,y,n+ch-1]:
end do:
for j to i do
n:=n+1: y:=y+1: tt:=tt,[x,y]:t1:=t1,[x,y,n+ch-1]:
end do:
else
for j to i do
n:=n+1:x:=x-1: tt:=tt,[x,y]: t1:=t1,[x,y,n+ch-1]:
end do:
for j to i do
n:=n+1:y:=y-1: tt:=tt,[x,y]:t1:=t1,[x,y,n+ch-1]:
end do:
end if:
end do:
for i to n do
if isprime(i+ch-1) then
p[i]:=disk(tt[i], 0.5, color=red)
else
p[i]:=disk(tt[i], 0.5, color=yellow)
end if:
end do:
c:=seq(p[i],i=1..n):
a:=plot([tt],color=blue):
if z=1 then
b:=textplot([t1]):
else b:=textplot([[0,0,ch],[x,y,n]]):
end if:
plots[display](a,b,c,axes=none);
end proc:
При значении второго параметра процедуры z=1 на диаграмму выводятся числа, иначе – лишь изображающие их цветные точки: красные – соответствуют простым числам, жёлтые – составным числам. Третий параметр ch указывает на число, которое будет находиться в центре спирали.
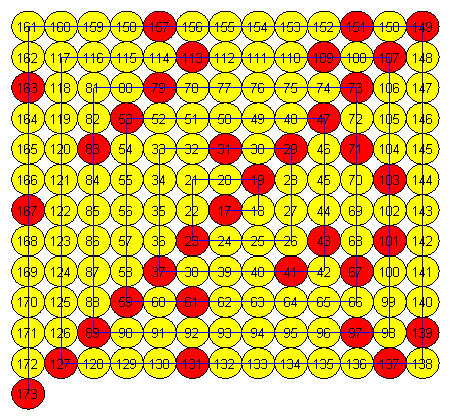
Рассмотрим, к примеру, шесть витков спирали Улама, начиная с числа 17.
> Ulam(6,1,17);
Мы ясно видим, что в скатерти Улама примечательно то, что простые числа стремятся выстроиться по диагоналям, образуя довольно длинные цепочки. Обнаружено, что эти цепочки являются вычисляемыми значениями некоторых квадратичных многочленов [4], например, (см. рисунок выше) или
(как в следующем случае) при x=0,1,2,3,4 и т.д.
> Ulam(7,1,41);
Процедура Ulam выполняется немного быстрее, если задать параметр z=0; в этом случае на график выводится только единица и последнее число рассматриваемой последовательности.
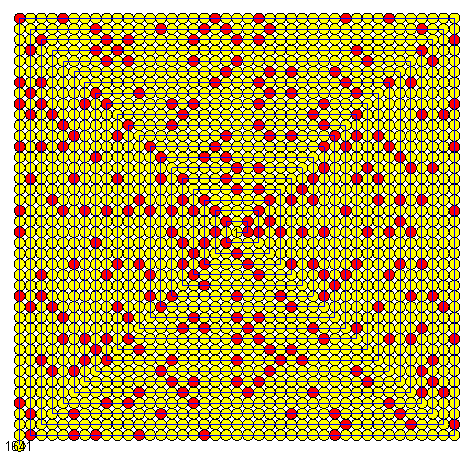
Следующая спираль имеет 20 витков, начинается с единицы, прочие числа (кроме последнего) в ней не отображены, но по цвету точек мы можем судить о расположении на скатерти простых чисел
> Ulam(20,0,1);
2. Спираль Сакса
В 1994 году Роберт Сакс, основываясь на скатерти Улама, разработал свой вариант спирали [5]. В ней целые неотрицательные числа выводятся не на квадратной, а на архимедовой спирали, и расположены они так, что квадрат целого числа воспроизводится один раз в каждом витке спирали (в спирали Улама мы встречаем два квадрата целого числа на витке).
Ниже предлагается Maple-процедура RS для воспроизведения спирали Сакса.
> restart:with(plottools):with(plots):
> rs:=proc(N,q)
local w,b,i,p,c:
if q=1 then w:=seq([i,sqrt(i)*2*Pi,i],i=0..N) else w:=seq([i,sqrt(i)*2*Pi],i=0..N) end if:
b:=plot((x/2/Pi)^2,x=0..sqrt(N)*2*Pi, coords=polar,axes=none,scaling=constrained,color=blue):
for i from 1 to N do
if isprime(i-1) then
if q=1 then p[i]:=textplot([w [i]], coords=polar,color=red):
else p[i]:=plot([w [i]], style=point, symbol=circle,symbolsize=10, coords=polar,color=red):end if:
else
if q=1 then p[i]:=textplot([w[i]], coords=polar,color=black):
else p[i]:=plot([w [i]],style=point, coords=polar,color=black,symbolsize=6):end if:
end if:
end do:
c:=seq(p[i],i=1..N):
plots[display](b,c);
end proc:
Эта процедура имеет следующие входные параметры: N (указывает сколько чисел изображать на спирали) и q (при q=1 на диаграмму выводятся числа, в противном случае – точки, соответствующие их положению). Простым числам на диаграмме соответствует красный цвет.
Изобразим, к примеру, на спирали Сакса шестьдесят пять целых чисел и добавим на диаграмму пару линий S и Р, играющих в данном геометрическом представлении особую роль.
> S:=seq([i^2,sqrt(i^2)*2*Pi],i=0..8):
P:=seq([i^2+i,sqrt(i^2+i)*2*Pi],i=0..8):
c:=plot([P],coords=polar,symbolsize=15,scaling=constrained,color=black):
b:=plot([S],coords=polar,symbolsize=15,scaling=constrained,color=black):
a:=rs(65,1):
display(a,b,c);
На графике видно, что все квадраты целых чисел (1, 4, 9, 16, 25, …) выстроились справа в один ряд, образуя как бы «нулевой луч», выходящий из полюса, обозначенного числом 1.
Этот луч также можно именовать «осью квадратов», так как числа на ней представляют собой произведения (1×1, 2×2, 3×3 и т.д.); в нашем обозначении это S-линия.
Последовательность чисел на линии S задается формулой при x=1..∞ .
В общем случае числовые ряды образуют кривые линии, берущие начало в центре спирали.
Вторая характерная линия, назовем ее P-линия – это кривая, на которой размещены числа 2, 6, 12, 20, 30, 42. Эти числа представляют собой произведения соседних пар чисел натурального ряда 1×2, 2×3, 3×4, 4×5, 5×6 и т.д.
Соответствующая последовательность или
при x=1..∞ .
Таким образом, числа, расположенные на S-линии, могут быть факторизованы с разницей между множителями, составляющей 0 (ноль), т.е. 1=1×1, 4=2×2, 9=3×3 и т.д., а числа на P-линии могут быть разложены на множители с разницей между ними 1.
Имея эти две характерные линии легко разобраться в сути многих других линий, обозреваемых на круглой скатерти Сакса. Так, рядом с S-линией находится линия S-1, все числа которой на единицу меньше (на соответствующем витке), чем те, которые расположились на линии S. Поэтому числа кривой S-1 могут быть представлены множителями с разницей в 2: 3=1×3, 8=2×4, 15=3×5, 24=4×6 и т.д. Формула последовательности при x=2.. ∞.
Найдём на рисунке следующую рассматриваемую кривую, которая содержит числа 4=1×4, 10=2×5, 18=3×6 и т. д.; здесь разница множителей 3. По понятным причинам, эту кривую удобно называть Р-2. Формула соответствующей последовательности при x=2..∞ .
Отметим теперь, что число 4 появилось на двух кривых: на одной как произведение 2×2, на другой как 1×4.
Мы можем и дальше продолжать отмечать кривые с увеличивающейся разницей между множителями.
И будем получать кривые S-1, S-2, S-3, …, и S+1, S+2, S+3, …, а также P-1, P-2, P-3, … и P+1, P+2, P+3, …
Сакс называет эти кривые кривыми произведений, потому что числа, расположенные на них состоят из произведений с фиксированной разницей между множителями.
Каждое целое число окажется, по крайней мере, на одной из этих кривых. Составные числа будут принадлежать более чем одной из этих кривых, а простые числа – только одной.
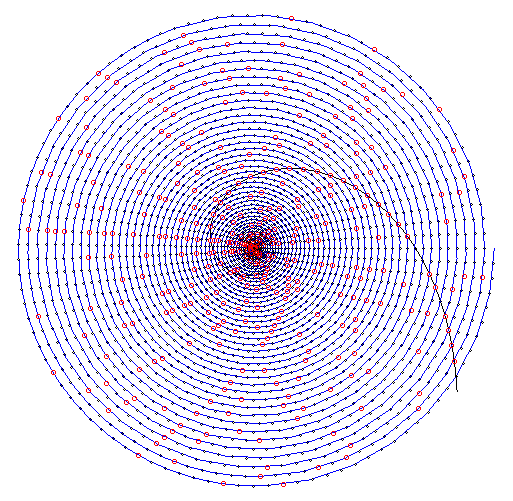
Пользуясь спиралью Сакса, можно исследовать структуру многих производящих последовательности простых чисел полиномов [6]. Например, ниже изображено положение на спирали Сакса членов последовательности , изучавшейся Эйлером и дающей много простых чисел.
> eu:=seq([i^2+i+41,sqrt(i^2+i+41)*2*Pi],i=0..50):
c:=plot([eu],coords=polar,symbolsize=15,scaling=constrained,color=black):
a:=rs(2500,0):
display(a,c);
Список использованных источников
1. Смирнов В.В., Спиридонов Ф.Ф. Компьютерная математика в исследовании простых чисел. // Современные научные исследования и инновации. – Февраль, 2013 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2013/02/20410
2. Смирнов В.В., Спиридонов Ф.Ф. Maple-инструменты исследования простых чисел-близнецов. // Современные научные исследования и инновации. – Февраль, 2013 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2013/02/22270
3. A visual analysis of prime number distribution [Электронный ресурс]. URL: http://www.ulamspiral.com/
4. Матиясевич Ю.В. Формулы для простых чисел. // Квант.- 1975. – № 5. – С. 5 – 13.
5. Sacks spiral [Электронный ресурс]. URL: http://www.numberspiral.com
6. Prime-Generating Polynomial [Электронный ресурс]. URL: http://mathworld.wolfram.com/Prime-GeneratingPolynomial.html