Введение
Изучение простых чисел ведется с глубокой древности, как учеными, так и служителями различных культов. Одним из первых проблему выявления простых чисел поставил древнегреческий ученый Эратосфен, позднее значительных результатов удалось добиться и другим исследователям, среди которых выдающимися считаются работы П. Ферма, Л. Эйлера, К. Гаусса, А. Лежандра, П. Чебышева и ряда других учёных.
Простые числа являются ключом к разрешению многих математических проблем и появляются в разных областях математики и ее приложениях. Криптография, имитационное моделирование, тестирование материнских плат персональных компьютеров – вот современный перечень практического применения простых чисел. Поэтому простые числа интересуют не только математиков, но и некоторые коммерческие организации, а также военных (разведку и контрразведку), ввиду их особого применения в области защиты информации [1].
О важности вопроса изучения простых чисел говорят и следующие факты:
1) за поиск больших простых чисел назначены крупные денежные премии;
2) некоторые из простых чисел являются запрещенными (законы об авторском праве запрещают их хранить и распространять).
Существуют открытые проекты поиска простых чисел-рекордсменов, в которых каждый может принять участие [2-4].
В данной работе используются средства известной системы компьютерной математики Maple для исследования числовых последовательностей, которые могут содержать простые числа. Предлагаются инструменты исследования в виде Maple-процедур, позволяющих наглядно представить состав и структуру таких числовых последовательностей.
Дальнейшее изложение материала ведётся с вставкой фрагментов диалога с компьютером в среде рабочего листа Maple. Начало ячеек ввода помечается угловой скобкой вида “>”, содержимое этих ячеек – команды Maple, окрашено в красный цвет. В среде Maple легко получить справку по поводу действия каждой команды; для этого достаточно выделить её и нажать клавишу [F1] на клавиатуре. Ячейка ввода, законченная символом “точка с запятой (;)”, при исполнении (клавиша [Enter]) возвращает ячейку вывода – результат вычислений, содержимое которого по умолчанию окрашено в синий цвет. Некоторые команды в ячейке ввода порождают графическое изображение. Возможности Maple в области математической графики очень богаты. Отчасти этим и объясняется предпочтение авторов, отданное данному математическому пакету.
1. Натуральные числа: простые и составные
Напомним, что положительные числа, используемые для счета, называют натуральными. Последовательность натуральных чисел является бесконечной. Рассмотрим часть этой последовательности.
> restart:
> N := {k $ k = 1..30};
N:={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}
Один из способов разделения всего множества натуральных чисел на непересекающиеся подмножества следующий: простые числа, составные числа и единица.
Простые числа – это те, которые делятся без остатка только на 1 и самих себя, составные числа – те, которые могут быть представлены через произведение простых сомножителей.
Рассмотрим множество целых чисел от 2 до 30.
> Z := { seq(k, k = 2..30) };
Z:={2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}
Выберем простые числа из этого множества.
> P := select( isprime, Z );
P:={2, 3, 5, 7, 11, 13, 17, 19, 23, 29}
Ни одно из них не разлагается на множители.
Теперь исключим простые числа из исходного множества. Это составные числа.
> C := remove( isprime, Z);
C:={4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30}
Каждое из полученных чисел раскладывается на множители.
> for k from 1 to nops(C) do C[k] = ifactor(C[k]): od;
4 = (2)^2
6 = (2)*3)
8 = (2)^3
9 = (3)^2
10 = (2)*(5)
12 = (2)^2*(3)
14 = (2)*(7)
15 = (3)*(5)
16 = (2)^4
18 = (2)*(3)^2
20 = (2)^2*(5)
21 = (3)*(7)
22 = (2)*(11)
24 = (2)^3*(3)
25 = (5)^2
26 = (2)*(13)
27 = (3)^3
28 = (2)^2*(7)
30 = (2)*(3)*(5)
Согласно «Основной теореме арифметики», впервые сформулированной и доказанной К. Гауссом в 1801 г. [5], такое разложение единственно. И это одна из причин, по которой математики не считают 1 простым числом. Ведь единицу можно добавлять в качестве сомножителя в любом количестве, и, тогда, о единственности разложения сказать затруднительно.
2. Простые числа на числовой прямой, решето Эратосфена
На первый взгляд расположение простых чисел в натуральном ряду кажется беспорядочным. Однако представим процесс нахождения простых чисел графически, воспользовавшись одним из древнейших методов нахождения простых чисел, называемым “Решето Эратосфена”.
Начать можно с изображения N натуральных чисел на числовой прямой. Затем произвести последовательные исключения (вычеркивания) всех чисел кратных простым. То есть вначале мы вычеркиваем все числа, кратные 2, затем все числа кратные 3, 5 и т.д. Вычеркивание будем производить при помощи синусоид, с периодом, кратным рассматриваемому числу.
Согласно правилу использования метода, вычеркивания производятся до числа, не превышающего квадрата наибольшего из простых делителей. Причина здесь в том, что для любого составного числа X наименьший целый делитель, кроме 1, расположен в пределах
Вот соответствующая Maple-процедура:
> with(plottools): with(plots):
nl:=proc(N)
local i,q,m,a,b,s,sn,c:
for i to N do
if isprime(i) then
q[i]:=disk([i,0], 0.5, color=red):
else
q[i]:=disk([i,0], 0.5, color=yellow):
end if:
m[i]:=textplot([i,0,i]):
end do:
a:=seq(q[i],i=1..N):
b:=seq(m[i],i=1..N):
m:=isqrt(N):
s:=1:
for i to m while s<m do
s:=ithprime(i):
sn[i]:=plot(s*sin(x*Pi/s),x=s..N,y=-m..m,color=COLOR(RGB,i/s,i/m,s/m))
end do:
c:=seq(sn[k],k=1..i-1):
display(a,b,c,axes=none);
end proc:
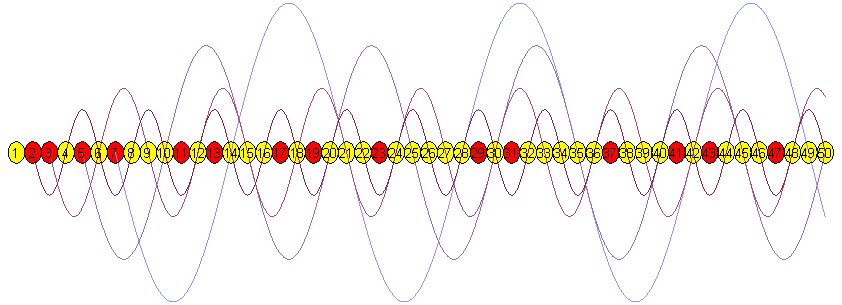
Вычеркнем, например, все составные числа среди целых в промежутке от 0 до 50.
> nl(50);
Красным цветом выделены простые числа. Для удобства вычеркивающим синусоидам назначены различные цвета и амплитуды.
Обобщая можно предложить следующий способ вычеркивания всех составных чисел, начиная с некоторого целого v>p, где p – заданное простое число и заканчивая .
1. Вычисляем произведение периодических функций вида
где i пробегает значения всех простых чисел не превышающих р.
2. Строим полученную синусоиду на числовой оси.
> ss:=proc(v)
local p,k,h,t,P:
if isprime(v) then
p:=v:h:=p:
else
p:=prevprime(v):h:=p:
end if:
while h>2 do
t:=prevprime(h):
p:=p,t:
h:=t:
end do;
P:=1:
for k to nops([p]) do
P:=P*sin(x*Pi/p[k])
end do:
plot(P,x=p[1]+0.5..p[1]^2,tickmarks = [[seq(i, i = 1 .. p[1]^2)],[]]);
end proc:
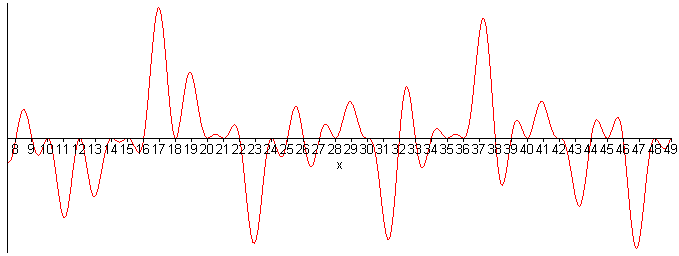
Пусть p=7, тогда . Выполненная процедура ss(7) возвращает график с вычеркнутыми составными числами в промежутке от 7 до 49.
Заметим, что на графике легко различить простые числа, отличающиеся между собой на 2, 4 и на 6 единиц. Такие разницы будут присутствовать и в дальнейшем.
3. Сравнимые по модулю и взаимно простые числа
Как простые, так и составные числа подчиняются ещё одному важному правилу: для данного целого отличного от нуля числа b, всякое целое число а единственным образом представимо в виде
а = bq + r , где 0≤ r < | b |. (1)
При этом число q называется неполным частным, а число r – остатком от деления а на b . Получим подобное представление для нашего множества простых чисел при делении каждого из них на 2.
> b:=2:
> for k from 1 to nops(P) do P[k] = b*cat(`*`)*cat(floor(P[k]/b))+cat(irem(P[k],b)): od;
2 = 2*1+0
3 = 2*1+1
5 = 2*2+1
7 = 2*3+1
11 = 2*5+1
13 = 2*6+1
17 = 2*8+1
19 = 2*9+1
23 = 2*11+1
29 = 2*14+1
Рассматривая последний результат, вспомним ещё одно определение: говорят, что целые числа a и b равноостаточны или сравнимы по модулю натурального числа m > 1, если a и b имеют одинаковые остатки от деления на m. В нашем случае видно, что все простые числа (кроме двойки) сравнимы по модулю 2, т.к. имеют остаток от деления на двойку, равный 1. Но, таковы также и все нечётные числа. Поэтому все простые числа, кроме 2, – нечётные.
Числа могут быть также взаимно просты. В этом случае их наибольший общий делитель равен единице. Например, взаимно простыми с числом 2 являются все нечётные числа.
> t:=2: sp:=NULL:
for i to nops(N) do
if igcd(N[i],t)=1 then sp:=sp,N[i]; fi:
od:
sp;
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29
В том числе, опять же, все простые, кроме числа 2.
Предложим вычислительный инструмент – процедуру для представления любого множества чисел в виде (1)
> sm:=proc(b,s)
local k:
for k from 1 to nops(s) do print(s[k] = b*cat(`*`)*cat(floor(s[k]/b))+cat(irem(s[k],b))): od;
end proc:
Например, представим каждое число из множества
> sa:={seq(k, k = 592..600)};
sa:={592, 593, 594, 595, 596, 597, 598, 599, 600}
в виде разложения (1) при делении на 23:
> sm(23,sa);
592 = 23*25+17
593 = 23*25+18
594 = 23*25+19
595 = 23*25+20
596 = 23*25+21
597 = 23*25+22
598 = 23*26+0
599 = 23*26+1
600 = 23*26+2
Следующая процедура выделяет из исходного множества числа, взаимно простые с предложенным числом.
> sc:=proc(t,ss)
local sp,i:
sp:=NULL:
for i to nops(ss) do
if igcd(ss[i],t)=1 then sp:=sp,ss[i]; fi:
od:
sp;
end proc:
Например, выделим из множества целых чисел Z взаимно простые с числом 6:
> sc(6,Z);
5, 7, 11, 13, 17, 19, 23, 25, 29
Представим каждое из этих чисел в виде разложения (1):
> sm(6,{%});
5 = 6*0+5
7 = 6*1+1
11 = 6*1+5
13 = 6*2+1
17 = 6*2+5
19 = 6*3+1
23 = 6*3+5
25 = 6*4+1
29 = 6*4+5
Проверим с помощью функции Эйлера, что количество чисел меньших 6 и взаимно простых с 6 равно двум:
> numtheory[phi](6);
2
Это числа 1 и 5.
Как видим, все целые числа взаимно простые с числом 6 входят в одну из двух арифметических прогрессий
> seq(6*n+5,n=0..10);# или seq(6*n-1,n=1..11), что то же самое
5, 11, 17, 23, 29, 35, 41, 47, 53, 59, 65
или
> seq(6*n+1,n=1..10);
7, 13, 19, 25, 31, 37, 43, 49, 55, 61
Эти прогрессии включают все числа, не делящиеся на 2 или 3, и поэтому каждое простое число, большее 3 входит в одну из этих прогрессий. В онлайн-энциклопедии целочисленных последовательностей [6] указано несколько способов получения обобщённой последовательности для обоих прогрессий, в том числе вычислением по формуле:
> seq((6*n+(-1)^n-3)/2, n=2..22);
5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43, 47, 49, 53, 55, 59, 61, 65, 67
4. Геометрическое представление простых чисел по заданному модулю
Использование сравнений по модулю допускает наглядное представление целых чисел с использованием не числовой прямой, как обычно, а числовой окружности [7]. Окружность при этом делится на b частей. Всякое целое число при делении на b даёт в качестве остатка одно из чисел 0, 1, 2, …, b-1; эти числа расставляются по окружности на равных расстояниях. Каждое число сравнимо с одним из этих чисел по модулю b и, следовательно, представляется соответствующей точкой. Два числа сравнимы, если изображаются одной и той же точкой. Мы представим их как лежащие на одном луче, начало которого располагается в центре окружности.
Ниже предлагается процедура cr, выстраивающая целые числа, сравнимые по модулю с b (второй аргумент) на лучах, проходящих через соответствующую точку окружности. Первым аргументом процедуры является количество изображаемых на луче чисел.
> restart:
> cr:=proc(t,b)
local i,pn,p,c1,w,n,j, ch:
n:=0:
for i to t do
for j to b do
n:=n+1:
pn[n]:= [i,evalf(j*2*Pi/b),n-1];
ch[n]:=pn[n][3]
end do
end do:
w:={seq(pn[k],k=1..t*b)}:
for i from 1 to nops(w) do
if isprime(ch[i]) then
p[i]:=plots[textplot]([w [i]], coords=polar,color=red):
else
p[i]:=plots[textplot]([w[i]], coords=polar,color=black):
end if:
end do:
c1:=seq(p[k],k=1..t*b):
plots[display](c1,axes=none);
end proc:
Например, изобразим на окружности по 10 чисел, сравнимых по модулю с числом 6. Красным цветом на графике помечены простые числа.
Мы видим, что все простые числа, кроме 2 и 3, попали на два луча, на которых располагаются всё те же последовательности чисел, описываемые формулами 6n-1 и 6n+1.
В теории чисел используется понятие “классы вычетов по модулю b“. Каждый такой класс содержит бесконечное количество сравнимых между собой целых чисел, объединенных одним соотношением (1), то есть при делении на b дающих одинаковый остаток r. В нашем примере каждый числовой луч соответствует классу вычетов по модулю 6.
5. Бесконечность последовательности простых чисел
Простые числа могут быть очень большими. Например, число, найденное в 1971 году [2] имеет вид:
> x:=2^19937-1:
`В этом числе`*cat(length(%))*`знака`;
В этом числе 6002 знака
Это одно из чисел Мерсенна, которые вычисляются по формуле , где n – натуральное число, и давно удерживают лидерство как самые большие известные простые числа. Устроим ему проверку (компьютеру потребуется некоторое время, возможно, пара минут).
> isprime(x);
true
Проверка показывает, что х – простое число.
В настоящее время наибольшее простое число (найдено в 2008 году) содержит 12 978 189 десятичных знаков [3]. Оно вычислено с помощью формулы для чисел Мерсенна как .
Если считать, что на одной странице книги обычного формата помещается около 2000 символов, то можно вычислить сколько страниц займёт это число в книге:
> `Это число в книге займет` * cat(irem(12978189,2000)) *`страниц`;
Это число в книге займёт 189 страниц
Однако чем дальше от начала натурального ряда, тем все реже встречаются простые числа. Известная гипотеза, высказанная Лежандром, утверждает, что количество простых чисел, не превосходящих данное натуральное число n, – можно приближенно оценить следующей функцией:
> p:=n->n/(ln(n)-1.08366);
Скорость ее возрастания постепенно (весьма незначительно) уменьшается:
> pp:=diff(p(n),n);
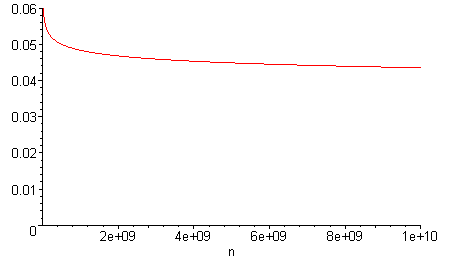
Для больших чисел график производной показывает уменьшение скорости роста функции Лежандра на десятые и сотые доли единицы при изменении n на порядок
> plot(pp(n),n=0..10^10,0..0.06);
Согласно гипотезе Лежандра количество простых чисел, не превосходящих 10000, будет примерно равно:
> p(10000.);
1230.514742
На самом деле: вот простые числа слева и справа от 10000:
> prevprime(10000);
9973
> nextprime(10000);
10007
Путем подбора устанавливаем
> ithprime(1229);
9973
То есть число 9973 – это 1229-е простое число в натуральном ряду. Таким образом, гипотеза Лежандра в данном диапазоне дает чуть завышенную, но достаточно точную оценку.
Действительно ли последовательность простых чисел бесконечна? Ответ на этот вопрос утвердительный. Доказательство бесконечности множества простых чисел следует из единственности разложения (1) всякого целого числа и присутствует уже у Евклида в его знаменитых “Началах”. Суть доказательства в следующем. Пусть p1, p2, …, pn – все известные нам простые числа. Перемножим их и прибавим единицу, получим число P = p1× p2× …× pn+1, которое больше любого известного простого числа. При этом Р не делится без остатка ни на одно из простых p1, p2, …, pn. Значит либо само это число Р является простым, либо делится на другое простое число, не включённое в известный набор. Например, нам известно только 8 простых чисел:
> restart: A:=seq(ithprime(k),k=1..8);
A:=2,3,5,7,11,13,17,19
Прибавим единицу к их произведению:
> a:=product(A[j],j=1..6)+1;
isprime(a);
a:=30031
false
Получили составное число, разлагаемое на простые множители:
> ifactor(a);
(59)(509)
Оба эти простые числа не были нам известны по условию задачи.
Литература
1. Найдена секретная экспонента для 12720 публичных ключей RSA. http://www.xakep.ru/post/58288/
2. Great Internet Mersenne Prime Search. GIMPS. Finding World Record Primes Since 1996. http://mersenne.org/
3. Еще раз о поиске простых чисел. http://habrahabr.ru/blogs/algorithm/114490/
4. Prime Grid. http://www.primegrid.com/forum_thread.php?id=3874
5. Дэвенпорт Г. Высшая арифметика: Введение в теорию чисел. – М.: УРСС, 2010. – 176 с.
6. The On-Line Encyclopedia of Integer Sequences. http://oeis.org
7. Курант Р., Роббинс Г. Что такое математика? – М.: МЦНМО, 2004. – 568 с.

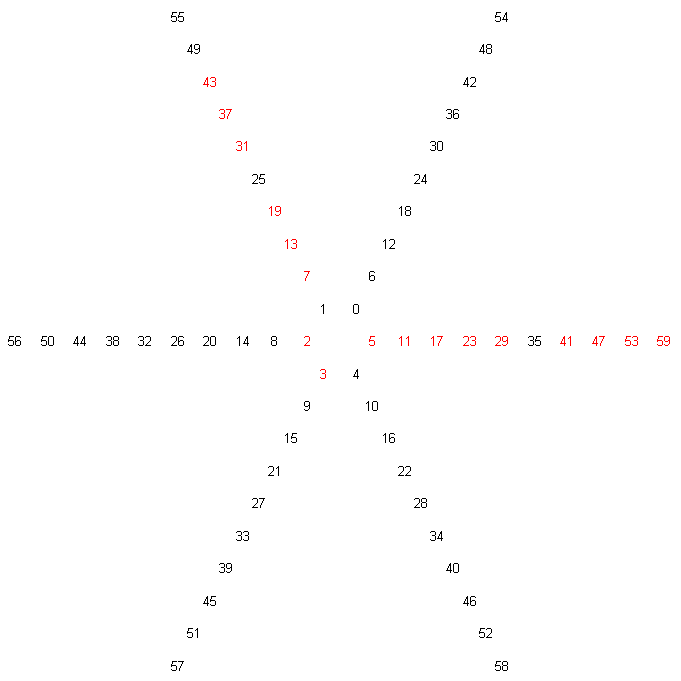
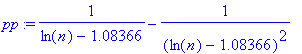
Огромное спасибо авторам! – Очень интересный материал. Пришлось немного помучаться, чтобы разобраться ( правда, не во всем :).
Текст Maple-процедур нужно вводить без “>”.
При построении графика с синусами Maple 17, почему-то, обрезает первый и последний кружок с числом.
Сначала лучше копировать текст процедуры в текстовый редактор (например “Блокнот”) и сравнить с тем, что написано на сайте. Почему-то происходит замена или потеря символов. (Например: при попытке построить окружность по 10 чисел, сравнимых по модулю с числом 6)
Работающий текст процедуры:
cr := proc (t, b) local i, pn, p, c1, w, n, j, ch; n := 0; for i to t do for j to b do n := n+1; pn[n] := [i, evalf(2*j*Pi/b), n-1]; ch[n] := pn[n][3] end do end do; w := {seq(pn[k], k = 1 .. t*b)}; for i to nops(w) do if isprime(ch[i]) then p[i] := plots[textplot]([w[i]], coords = polar, color = red) else p[i] := plots[textplot]([w[i]], coords = polar, color = black) end if end do; c1 := seq(p[k], k = 1 .. t*b); plots[display](c1, axes = none) end proc;
cr(10, 6);