В последние годы ведется активная работа по разработке квантовых компьютеров. Квантовые компьютеры способны взломать криптосистемы, которые основаны на задаче факторизации целых чисел. Это значит, что квантовые компьютеры способны взломать систему RSA, которая является одной из самых распространённых криптосистем открытого ключа.
Взлом криптосистемы RSA вызовет полный хаос[1].
Одной из альтернатив RSA являются схемы цифровой подписи (Hash Based Digital Signature Schemes), основанные на хешировании. Безопасность этих системы основана на безопасности криптографической хеш-функции. Вначале была предложена одноразовая схема подписи Лэмфорта. Данная система работает следующим образом: выбираем 2n случайных чисел Xij, где 1≤i≤n и j = {0, 1}. Высчитываем Yij = h(Xij), h – это функция хеширования: h:{0,1}* ->{0,1}s, Yij – это открытый ключ, Xij – закрытый ключ. С помощью этих ключей шифруем сообщение M = (0,1)n.
Ключи и подпись в этой криптосистеме очень большие[2], что делает данную систему не эффективной.
Для увеличения эффективности была предложена другая одноразовая схема- Winternitz One-time Signature Scheme. Данная система работает следующим образом: выбирается параметр w ∈ N, и вычисляется r = [s/w]+[([log2 [s/w]] + 1 + w)/w]. После выбираются r случайных чисел X1, X2, … Xr ∈{0,1}s, объединяя их мы получаем закрытый ключ – X. Открытый ключ Y, является объединением Yi, где Yi = h2w−1(Xi). Сообщение M делится на s/w блоков b1, …, bs/w длиной w. Контрольная сумма вычисляется следующим образом: C = -bi.
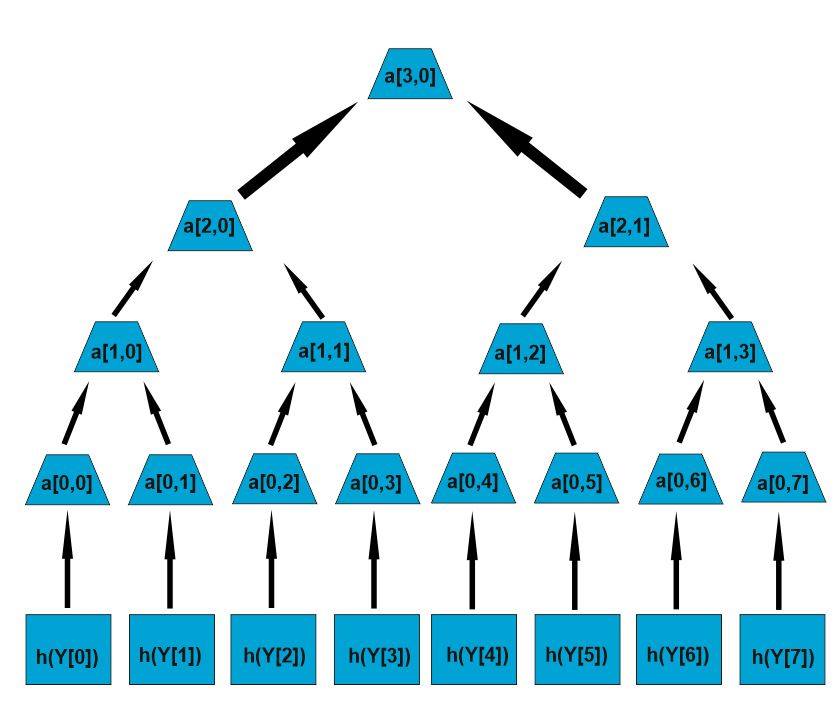
Огромная проблема данных одноразовых схем, передача открытого ключа. Поэтому была предложена криптосистема Меркле, в данной системе один открытый ключ можно использовать много раз. С помощью одного открытого ключа K подписывается число сообщений N, являющееся степенью двойки N=2n. Генерируются ключи Xi и Yiдля N записей и вычисляется hi=h(Yi), используя эти данные мы строим дерево Merkle.
Рис 1
Каждый узел это хеширование его детей: a1,0 = h(a0,0|| a0,1); Корень дерева an,0 – корень дерева используется в качестве открытого ключа, public.
Для получения подписи signew сообщения M мы используем криптосистему одноразовой подписи, с ключами Xi и Yi. a0,i= H(Yi) – лист дерева. P это путь от узла a0,iдо корня, данный путь состоит из n+1 узлов, P0= a0,i, а Pn= an,0. Для того, чтобы вычислить путь нам нужны все P0, …, Pn. Pn+1 = h(Pi||authi), authi этобратский узел для Pi. Подпись письма M вычисляется следующим образом: sig = (signew ||auth0||auth1||…||authn−1). Для верификации подписи проверяется signew и вычисляются Pi, если полученное значение Pn равно public, подпись корректна.
Закрытый ключ системы Меркле состоит из 2n одноразовых ключей, хранение такого размера данных довольно не удобно. Был предложен вариант использовать PRNG – генератора псевдо случайных чисел, благодаря этому достаточно хранить только семя данного PRNG.
В данном случае каждый ключ одноразовой подписи должен быть сгенерирован дважды, один раз для генерации открытого ключа и второй раз для подписи сообщения. PRNG получает семя s1 и выдает новое семя s2 и случайное число r.
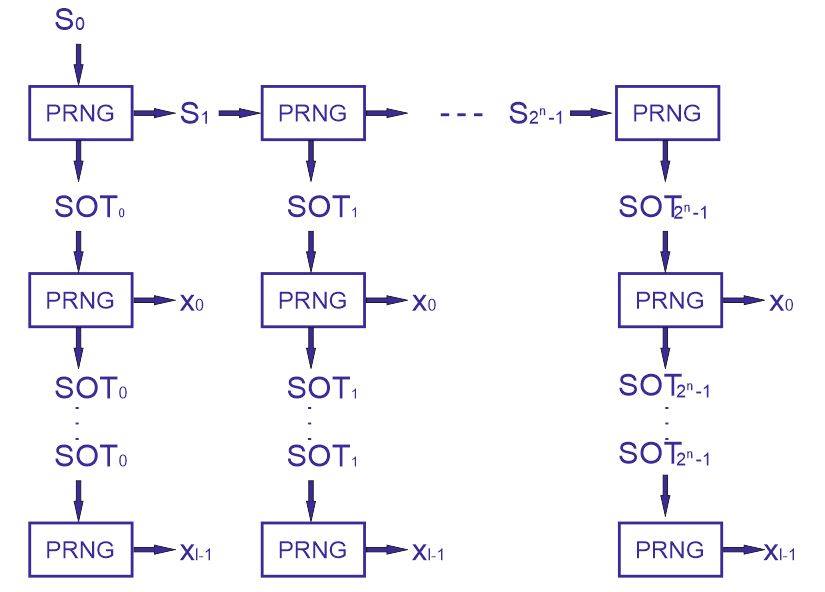
Для генерации ключа одноразовой подписи, мы выбираем семя s0 случайным образом, с помощью siмы вырабатываем soti, следующим образом:
PRNG(si) = (soti , si+1) 0 ≤ i <2n.
sotiкаждый раз меняется когда мы запускаем генератор псевдо случайных чисел. Т.е. для нахождения ключа Xi, достаточно знание только siи т.д.
Процесс генерации одноразового ключа показан на рисунке рис2. :
Рис 2
Можно усомниться в безопасности данной схемы, т.к. выходит множество работ по взлому PRNG квантовыми компьютерами, которые считались безопасными против атак стандартных компьютеров[3]. Была показана полиномиальная квантовая атака времени на PRNG Blum-Micali, который считается безопасным от угроз со стороны классических компьютеров. Данная атака использует методику, Гровера вместе с квантовым дискретным логарифмом, и способна восстанавливать предыдущие и будущие значения на выходе генератора при данной атаке, тем самым
взламывает его. Данную атаку можно адаптировать и к другим PRNG, таким как генераторы Блюма-Микали с несколькими предикатами с жесткими запросами и
генераторам конструкции Blum-Micali, а также к сценариям, где требования
к битам ослаблены. Такие атаки представляют угрозу безопасности псевдослучайных
генераторов, используемых во многих криптосистемах реального мира. Т.е. исходя из этого система Merkle с такого типа PRNG не является безопасной против атак квантовых компьютеров.
Исходя из того, что система Merkle разрабатывается против атак квантовых компьютеров мы предлагаем использовать квантовые компьютеры для доработки и оптимизации данной системы. Мы предлагаем использовать квантовый алгоритм генерации псевдо случайных чисел в системе Меркле.
Был предложен новейший генератор псевдослучайных чисел, основанный на квантовых случайных блужданиях[4]. Данный PRNG основан на уравнениях квантовых случайных блужданий (QRW), и, следовательно, алгоритм генерации прост и скорость вычислений является быстрой.
Как было указано выше генератор случайных чисел для интеграции с криптосистемой Меркле должен работать следующим образом: PRNG(si) = (soti , si+1) , 0 ≤ i <2n
В качестве семени si возьмем параметры (E,( α, β),p, θ) одномерных дискретных квантовых случайных блужданий (QRW) на окружности с E узлами и генерируем распределения вероятностей. Здесь p – номер шага QRW, чье значение принадлежит положительной целочисленной области. E – номер узла круга, значение которого также принадлежит положительной целочисленной области и являются амплитудными параметрами состояний монеты, которые являются комплексными числами и удовлетворяют ограничению:
| α2| + | β 2| = 1
θ ∈ {0,2π} – параметр операторы монеты.
Мы преобразовываем распределение вероятностей в последовательность:
sc1 = [P11, P12, … P1E, P21, P22, … , P2E, … , PK1, PK2, PKK]
Повторяя все заново получаем последовательность и группируя все сгенерированные последовательности распределения вероятностей SCi в последовательность случайных чисел, получаем sot = (sc1, sc2, …, scg).
Данный PRNG основан на уравнениях квантовых случайных блужданий (QRW), и, следовательно, алгоритм генерации прост и скорость вычислений является быстрой. Предлагаемый PRNG успешно прошел такие испытания как NIST. По сравнению с представителем PRNG на основе квантовых хаотических карт (QCM)[5], данный PRNG преимущества, такие как более высокая статистическая сложность и повторяемость.
Это значит, что система Merkle основанная на данном PRNG, является безлопастной и более эффективной.
РАБОТА ВЫПОЛНЕНА В РАМКАХ НАУЧНОГО ГРАНТА «НАЦИОНАЛЬНОГО НАУЧНОГО ФОНДА ШОТА РУСТАВЕЛИ» YS2015.
Библиографический список
- Гагнидзе А.Г., Явич М.П., Иашвили Г.Ю. Пост-квантовые криптосистемы // Современные научные исследования и инновации. 2016. № 5 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/05/67264
- A. Gagnidze, M. Iavich, G. Iashvili, Some Aspects of Post-Quantum Cryptosystems, Abstract book, EURO-ASIA FORUM IN POLITICS ECONOMICS AND BUSINESS – 2016, JULY 21-22, 2016, BELGRADE, SERBIA
- Change GUEDES, E., DE ASSIS, F., & LULA, B. (2013). Quantum attacks on pseudorandom generators. Mathematical Structures in Computer Science, 23(3), 608-634. doi:10.1017/S0960129512000825
- Yu-Guang Yang & Qian-Qian Zhao , Novel pseudo-random number generator based on quantum random walks, Scientific Reports 6, Article number: 20362
- Akhshani, A., Akhavan, A., Mobaraki, A., Lim, S. C. & Hassan, Z. Pseudo random number generator based on quantum chaotic map. Commun. Nonlinear Sci. Numer. Simulat. 19, 101–111 (2014).