В настоящее время многие ведущие ученые и эксперты активно работают над созданием квантовых компьютеров. Недавно была опубликована статья о том, что корпорация GOOGLE, совместно с NASA и ассоциацией USRA (Universities Space Research Association), подписали контракт о производстве квантовых процессоров с компанией D-Wave. D-Wave 2X – это новейший квантовый процессор, который содержит 2048 физических кубитов. Для выполнения вычислений в данном процессоре используются 1152 кубита.
Каждый дополнительный кубит в два раза увеличивает площадь поиска данных, следовательно, значительно повышается и скорость их вычисления. Исходя из вышесказанного, квантовые компьютеры вероятно смогут разрушить большую часть, если не абсолютно все традиционные криптосистемы, которые широко используются в практике. Конкретно, системы, основанные на задаче факторизации целых чисел (например, RSA). Некоторые криптосистемы, как система RSA с четырех тысячными битными ключами, считаются полезными для защиты классических больших компьютеров от атак, но вероятно являются абсолютно бесполезными против атак на большие квантовые компьютеры.
Криптосистема RSA используется в разных продуктах, на разных платформах и в различных сферах. На сегодняшний день данная криптосистема интегрируется во многие коммерческие продукты, количество которых растет с каждым днем. Также система RSA активно используется в операционных системах от Microsoft, Apple, Sun и Novell. В аппаратном исполнении RSA алгоритм используется в защищенных телефонах, Ethernet, сетевых платах, смарт картах, а также широко используется в криптографическом аппаратном обеспечении. Вместе с этим, данный алгоритм является частью основных протоколов защищенных коммуникаций Internet, в том числе S/MIME, SSL и S/WAN, и также используется во многих организациях, например, в правительственных, в банках, в большинстве корпораций, в государственных лабораториях и университетах.
Технология шифрации RSA BSAFE используется приблизительно 500 миллионами пользователей во всем мире. Так как в основном, в технологиях шифрования используется RSA алгоритм, то его можно считать одной из самых распространённых криптосистем открытого (public) ключа с тенденцией развития вместе с развитием Internet.
Исходя из этого, разрушение RSA повлечет за собой легкий взлом большинства продуктов, что может перерасти в полный хаос.
Разработаны различные “устойчивые к квантовым атакам” альтернативы системы RSA. Но на сегодняшний день на данные системы зафиксирован целый ряд успешно проведенных атак.
Одной из альтернатив являются схемы цифровой подписи, основанные на хешировании (Hash-based Digital Signature Schemes). Безопасность этих системы зависит от безопасности криптографической хеш-функции. Была предложена одноразовая схема подписи Лэмфорта “Lamport One-Time Signature Scheme “[1].
В данной схеме, чтобы подписать сообщение M = (0,1)n , нужно выбрать 2n случайных чисел Xij, где 1≤i≤n, а j = {0, 1}. Для всех i и j высчитывается Yij = h(Xij), где h – это хеш-функция: h:{0,1}* ->{0,1}s Yij – это открытый ключ, Xij – закрытый ключ. Для сообщения M = m1,m2, …,mn, где mi ∈ {0, 1}, если mi = 0 , то sigi = Xi0, в другом случае sigi = Xi1. Подпись sig – это объединение все sigi; sig = (sig1||sig2||…||sign), в случае верификации подписи, если h(mi) = 0, то h(sigi) должно быть равно Yi0, в другом случае h(sigi) должно быть равно Yi1.
Основной и серезный недостаток этой схемы – это большой размер ключей. Для того, чтобы достичь безопасность O(280), общий размер открытого и закрытого ключей должен быть 160∗2∗160 bits = 51200 bits, что в 51200/1024=50 раз больше, чем в случае RSA. Также стоит отметить, что размер подписи в данной схеме также намного больше, чем в случае RSA.
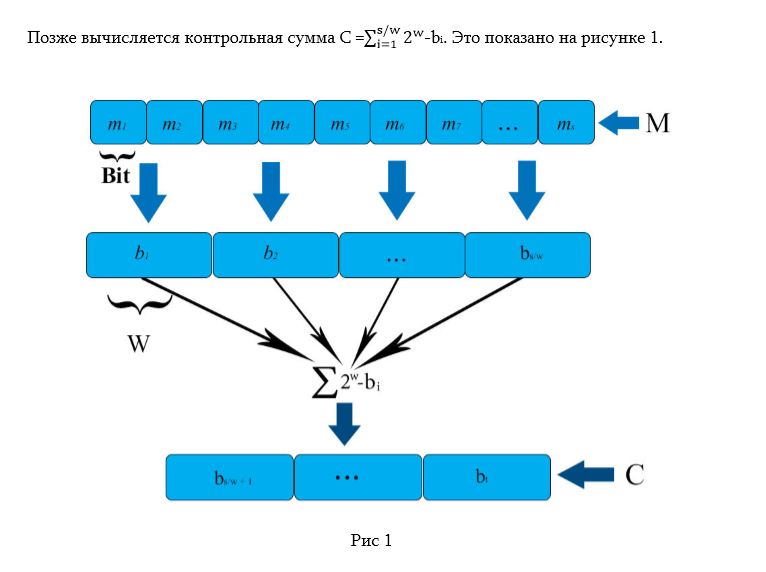
Для уменьшения размера подписи была предложена одноразовая схема подписи Винтерница ( Winternitz One-time Signature Scheme). В данной схеме мы выбираем параметр w ∈ N, и вычисляется r = [s/w]+[([log2 [s/w]] + 1 + w)/w]. Выбираем r случайных чисел X1, X2, … Xr ∈{0,1}s, объединение которых X является закрытым ключом. Высчитываются Yi = h2w−1(Xi), открытым ключом является Y = h(Y1||…||Yr). Сообщение M разделено на s/w блоков b1, …, bs/w длиной w, если нужно, слева добавляются нули.
Бинарное представление C разбивается на [([log2 [s/w]] + 1 + w)/w] блоков, bs/w+1, …, br длины w. Вычисляется sigi= hbi(Xi) для i = 1, …, r, подпись письма – это sig = (sig1||…||sigr). Для верификации подписи высчитываются: b1, …, br. Для i = 1, …, r вычисляется signewi= h2w−1−bi(sigi) = h2w−1−bi(hbi (Xi)) = h2w−1(Xi) = Yi, если h(signew1, …, signewr)=Y, то подпись верна.
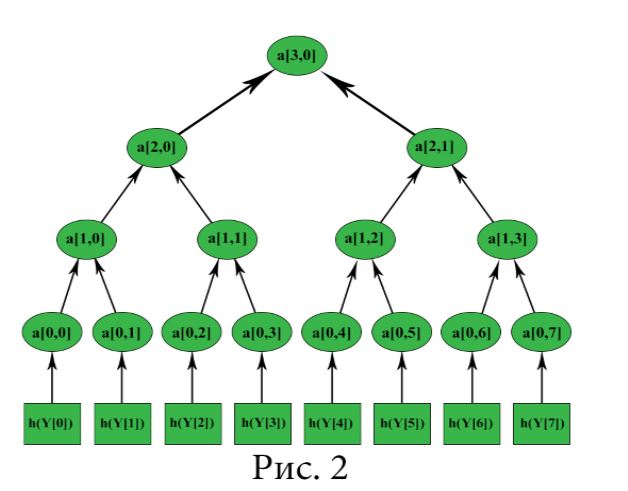
Самая большая проблема одноразовых схем подписей — это передача открытого ключа. Необходимо удостовериться в том, что открытый ключ не был изменен, поэтому нужно использовать как можно меньше открытых ключей и сделать их покороче. Меркл предложил криптосистему, где один открытый ключ можно использовать для множества сообщений. В данной криптосистеме открытый ключ K используется для подписи конкретного числа сообщений. Число сообщений должно быть степенью двойки, т.е. N=2n. В первую очередь, нужно сгенерировать ключи Xi и Yiдля N записей и вычислить hi=h(Yi), с помощью этих данных строится дерево- Merkle Tree, рисунок 2.
aij – это узел дерева.hi– это листья дерева. Узлы дерева являются объединением своих детей: a1,0 = h(a0,0|| a0,1); мы строим дерево с 2n листами и 2n+1-1 узлами. Корень дерева an,0 является открытым ключом – public.
Сообщение M подписывается одноразовой системой подписи, используя пару ключей Xi и Yi, в результате мы получаем signew. a0,i= H(Yi) – лист хеш-дерева. Путь от a0,i до корня назовем P, состоящий из n+1 узлов, P0= a0,i, а Pn= an,0 = public. Для вычисления этого пути нам нужны все дети узлов P0, …, Pn. Pn+1 = h(Pi||authi), где authi - братский узел Pi. Подпись письма будет: sig = (signew ||auth0||auth1||…||authn−1). При верификации записи проверяется signew сообщения M, если она верна, вычисляются P0, …, Pn, если Pn равен открытому ключу public, то подпись верна.
Последние годы ученые работают над улучшением схемы Меркле (Merkle Signature Scheme), достигнуты хорошие результаты по времени подписи и верификации сообщения [2,3], но несмотря на это, размер подписи является очень большим по сравнению с схемами подписи DSA и RSA.
Также одной из решений проблем, связанных с пост-квантовой криптографией, представляют McEliece – систему с открытыми ключами, которая в свою очередь основана на теории алгебраического кодирования. Разработана данная система в 1978 году Робертом Мак-Элисом. Данная система является первой системой шифрования с использованием процесса рандомизации. Несмотря на то, что алгоритм не получил широкого признания в класической криптографии, он является кандидатом для использования в постквантовой криптографии.
В данной системе открытый ключ – (Gnew, t), а закрытый ключ– (S, G, P), где G- это k x n порождающая матрица (generator matrix) для кода C. C – это случайный двоичный (n, k)-линейный код, способный исправить t ошибок. N- это количество кодовых слов, k – размерность C. S – случайная k x k двоичная невырожденная матрица. P – случайная n x n двоичная матрица перестановок. Gnew = S * G * P; k x n матрица. Для шифрования сообщения нужно сообщение m зашифровать как двоичную строку длины k; cyp = m x Gnew; генерируется случайный n-битовый вектор ошибки v весом t. Шифр вычисляется как: c= cyp+v. Для расшифровки вычисляется cyp = c*P-1 ; С помощью алгоритма расшифровки C вычисляется mnew= m*S => m= mnew*S-1
На сегодняшний день уже выявлены успешные атаки на данную криптоситему.
Докторант Дублинского университета (DCU) Неил Костиган (Neill Costigan) при поддержке Irish Research Council for Science, Engineering and Technology (IRCSET), а также профессора Майкла Скотта (Michael Scott), члена Science Foundation Ireland (SFI) успешно смогли провести атаку на данный алгоритм. Для этого им понадобилось 8000 часов процессорного времени. В атаке принимали участие представители еще четырех стран. Ученые выяснили, что начальная длинна ключа в данном алгоритме недостаточна, и должна быть увеличена.
Также эту систему нельзя использовать для шифровки одного и того же сообщения два раза и для шифровки сообщения, когда известна его связь с другим сообщением [4].
Из вышесказанного видно, что на сегодняшний день мы не готовы для перевода криптосистем в пост-квантовую эпоху. В ближайшем будущем мы не можем быть уверены в надежности представленных систем.
Необходимо отметить важность спектра эффективности. На сегодняшний день эксперты достигли довольно хороших результатов в скорости выполнения алгоритма. По результатам исследования становится ясно, что предложенные пост-квантовые криптосистемы сравнительно мало эффективны, алгоритмы реализации требуют намного больше времени для их выполнения и верификации.
Неэффективная криптография наверное может быть приемлемой для обычного пользователя, но она не может быть таковой для интернета серверов, которые обрабатывают тысячи клиентов в секунду. У Google на сегодняшний день существуют проблемы с текущей криптографией. Несложно представить, что будет, когда на реализацию крипто алгоритмов будет уходить больше времени.
На развитие и улучшение современных криптосистем уйдут годы. К тому же, на них все время фиксируются успешные атаки. Когда определяется функция шифрования, и она становится стандартом, ей нужна реализация соответствующего программного, а в большинстве случаев, и аппаратного обеспечения.
Во время реализации необходимо обеспечить не только корректную работу функции и скорость ее эффективности, но также и избежание любого вида утечек. Недавно зафиксированы успешные «cache-timing» атаки на системы RSA и AES, вследствие чего компания Intel добавила AES инструкции в свои процессоры.
Система McEliece является уязвимой к атакам, связанным с утечками (side channel attacks). Была показана удачная атака по времени (timing attack) на алгоритм Паттерсона [5]. Данная атака не выявляет ключ, но выявляет вектор ошибки, что позволяет успешно расшифровать шифр сообщения.
Как мы видим, для создания и реализации безопасных и эффективных пост-квантовых криптосистем необходимо провести довольно большую работу.
РАБОТА ВЫПОЛНЕНА В РАМКАХ НАУЧНОГО ГРАНТА «НАЦИОНАЛЬНОГО НАУЧНОГО ФОНДА ШОТА РУСТАВЕЛИ» [№ YS15_2.1.2_9].
Библиографический список
- Coppersmith, D., Stern, J., and Vaudenay, S.: The security of the birational permutation signature schemes. Journal of Cryptology (1997).
- E. Dahmen, M. Dring, E. Klintsevich, J. Buchmann, L.C. Coron-ado Garca. CMSS – an improved merkle signature scheme. Progress in Cryptology – Indocrypt 2006, 2006.
- E. Klintsevich, K. Okeya, C.Vuillaume, J. Buchmann, E.Dahmen. Merkle signatures with virtually unlimited signature capacity. 5th International Conference on Applied Cryptography and Network Security – ACNS07, 2007
- T. Berson. Failure of the McEliece public-key cryptosystem under message-resend and related-message attack. Springer-Verlag, 1997.
- F. Strenzke, E. Tews, H. Molter, R. Overbeck, and A. Shoufan. Side Channels in the McEliece PKC. In 2nd Workshop on Post-Quantum Cryptography. Springer, 2008.
Количество просмотров публикации: Please wait