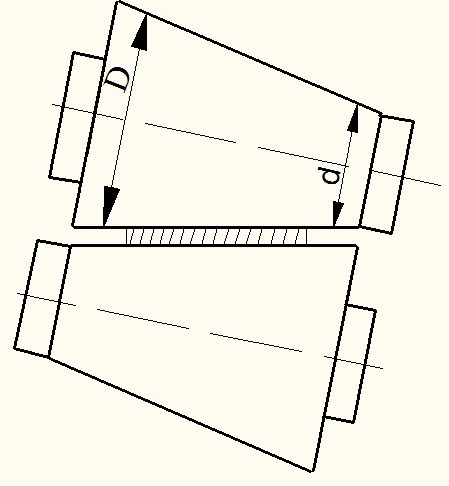
Процесс прокатки в валках с обратной конусностью характеризуются тем, что при прокатке в полосе обеспечивается более равномерное распределение физико-механических свойств, обусловленное тем, что течение металла ненаправленно вдоль продольной оси полосы, т.е. по направлению прокатки (рисунок 1). Известно, что при прокатке в цилиндрических валках зерна в основном вытягиваются в направлении прокатки, т.е. в продольном направлении, и как следствие, приводит к различию механических свойств в продольном и поперечном направлениях.

Рисунок 1 – Схема прокатки полосы в валках с обратной конусностью

Различие механических свойств (анизотропия) ухудшает свойство металла, как например свойство штампуемости листового материала при последующей штамповке листового металла (образование фестонов).
Поэтому разработка принципиально новых способов прокатки направленных на улучшение физико-механических свойств остается одним из основных задач прокатного производства. Одним из основных задач при разработке технологического процесса прокатки полосы в валках с обратной конусностью являются определения удельного или контактного и полного давления металла на валки для рационального установления режимов обжатия, определения запаса прочности материала валков и необходимой мощности оборудования.
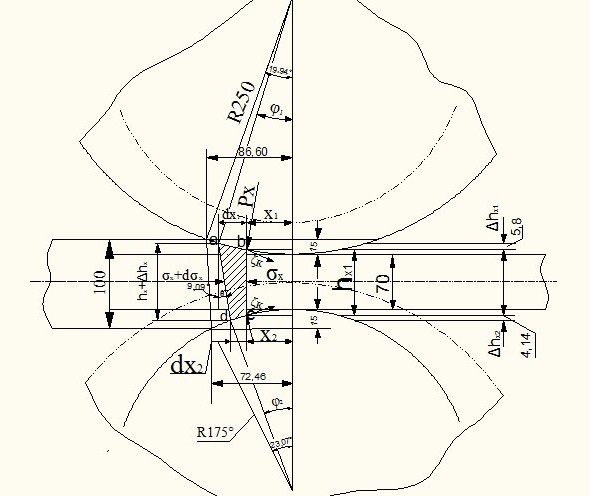
Для определения контактного (удельного) давления используем метод совместного решения дифференциальных уравнений равновесия и условия пластичности, подробно изложенный в работе Целикова А.И. [1]. Для этого в очаге деформации прокатываемого металла выделим некоторый элемент abcd ограниченный поверхностью валков и двумя плоскостями, один из которых перпендикулярно, а другой установлен относительно направлению прокатки, проведенных на бесконечно малом расстоянии друг от друга dx1 и dx2. Центральными углами выделенного сечения по отношению к линиям, соединяющими с центрами валков, будут φ1 и φ2(рисунок 2).

Рисунок 2 − Элементарный объем, выделенный в очаге деформаций полосы

Рассмотрим, какие силы действуют на выделенный элемент abcd, находящийся в равновесии. Cо стороны валков на элемент будет действовать вертикальная сжимающая сила , а в направлении, перпендикулярном поверхности валков, силы ,  . При этом ширину прокатываемого элемента равной единице и уширением пренебрегаем. 
Для упрощения расчета контактного давления рассмотрим зону, где силы трения совпадают с направлением прокатки, т.е. зону отставания. Хотя возможно существование зоны опережения. Но ввиду сложной формы очага деформации ограничимся зоной отставания.
С правой части полосы на выделенный элемент действует сила , 
где у_x – среднее нормальное напряжение сжатия в прокатываемом металле по сечению bc; 
h_x  − высота сечения bc. 
В плоскости ad, т.е. по высоте сечения ()/ cos и,

где и − угол наклона плоскости ad к вертикальной оси у будет действовать сила .

Сумма горизонтальных проекций всех сил на выделенный элемент по условию статики при равномерном движении должна быть равна нулю и может быть выражена в следующем виде:

,

где индексы 1 и 2 обозначают следствия действий на элемент двух валков: со стороны большего и меньшего диаметров. После преобразования, пренебрегая бесконечно малыми величинами, получим:

=0.

Чтобы решить данное уравнение, нужно иметь зависимость между удельным давлением р_х и напряжением _х. Для этого используют основное уравнение условия пластичности в следующем виде:

где  и  – главные нормальные напряжения;– сопротивление пластической деформации, с учетом влияния скорости деформаций, температуры и степени деформаций; 
- коэффициент, учитывающий влияние среднего главного напряжения  ₂ (принимаем =1,15).
Считая за главные напряжения в выделенном элементе вертикальные и горизонтальные напряжения, получим следующие: р_х =  и  = , тогда условие пластичности примет вид:

р_х -  = ,

дифференцируя это, находим:

dр_х=d.

Подставляя в уравнение равновесия, получим:

=0.

Установим зависимость между,котороеможно записать следующим образом:

; ; отсюда  и 

Подставляя вышеприведенные уравнения, и учитывая, что t_х= мp_x, 
где м – коэффициент контактного трения, получим:

, или

Принимаем приближенно следующее соотношения между абсолютными обжатиями со стороны верхнего (большего), нижнего (меньшего) валков с суммарным обжатием: и , где общее элементарное абсолютное обжатие. Подставляя данные соотношения в предыдущее уравнение, получим:

Для упрощения решения этого уравнения с достаточной степенью точности для практических расчетов полагаем углы   постоянными по всей дуге захвата, и равным половине угла захвата полосы т.е.φ₁ = 0,5α₁ и φ₂=0,5α₂ и приравниваем дугу к хорде. Для упрощения записи основного уравнения введем следующие обозначения:

.

Тогда, получим 

Следует отметить, что в разность равен разности сечений ad и bc. Из геометрических соображений нетрудно установить, что разность сечений равно значению 
Подставляя данное соотношение, и после разделения переменных, получим следующее: 

После разделения переменных получим:

После преобразования окончательно получим:

Для упрощения уравнения введем следующее обозначение δ^*=, 
тогда: после интегрирования которого, получим:
, 
отсюда
Постоянную С определяемые граничных условий, полагая, что на входе в очаг деформации при  удельное давление =,отсюда . Следует отметить, что если на прокатываемый металл со стороны входа не действуют какие – либо внешние силы, помимо валков (натяжение отсутствует), то  подставляя значение С предыдущее уравнения окончательно получим :

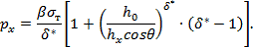
Таким образом, получена формула для определения распределения контактного давления при прокатке полосы в валках с обратной конусностью. Как и в формуле для определения контактных давлений при прокатке в цилиндрических валках, в полученную формулу входит параметр δ^*, куда входят значения и, δ₁ и δ_2, которые характеризуют процесс прокатки в валках с обратной конусностью. Полученное уравнение будет справедливо лишь до нейтрального слоя, пока направление сил трения не изменит свой знак на противоположный. Для зоны опережения также как и при традиционной прокатке в цилиндрических валках уравнение сразу можно написать, меняя знаки в последнем уравнений перед членами, содержащими силу трения (δ^*), т.е: 

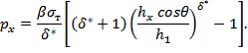
Анализ полученных формул для определения контактных давлений показывает небольшое снижение контактных давлений при прокатке в валках с обратной конусностью, которое прежде всего связано со снижением сил контактного трения (из-за уменьшения площади контактной поверхности), так как величина δ^* зависит от величины угла θ, характеризующий разность диаметров валков и в свою очередь форму очага деформаций. Контактная площадь между полосой и валками при прокатке в конических валках будет меньше, по сравнению в цилиндрических валках из-за меньшей длины дуги контакта со стороны меньшего диаметра конических валков.
В результате процесса прокатки в валках с обратной конусностью суммарная сила прокатки будет меньше, чем при прокатке в цилиндрических валках.
Уравнение для определения контактных удельных давлений выведено при тех же допущениях, что и прокатке в цилиндрических валках, изложенных в работе [1]. Следует отметить, что при φ₁= φ₂ т.е δ₁= δ₂ угол θ=0, и δ^*= δ, и в результате получим известную формулу для определения контактных напряжений при прокатке в цилиндрических валках. Поэтому уравнение, полученное в данной работе, вполне справедливо для определения удельного и полного усилия при прокатке полосы в валках с обратной конусностью.
Выводы. Получены формулы для определения распределения контактных давлений при прокатке полосы в валках с обратной конусностью, как со стороны опережения металла, так и со стороны отставания. Полученную формулу можно использовать при разработке технологии прокатки заготовок в валках с обратной конусностью.

1. Целиков А.И. Теория расчета усилий в прокатных станах. М. Металлургия. .494 с.

Все статьи автора «Сундетбаева Марал Амантурлиевна»