Общепризнанные мнения и то, что считают делом давно решенным, чаще всего заслуживает исследования.
В электростатике общепризнанно мнение о безусловной верности полевых граничных условий (они считаются верными в электродинамике и в радиофизике): на границе раздела двух сред нормальные составляющие вектора D и касательные составляющие вектора E остаются неизменными. Другие составляющие этих векторов претерпевают разрывы [1-3].
Однако безусловная верность условий, как это обычно принято в математике, совершенно не подходит для физики, главной задачей которой является поиск причин всего существующего и установление закономерных связей «причина-следствие» (по Аристотелю – истинное знание есть знание причин).
Существующее положение с трактовкой граничных условий электростатики (и электромагнетизма в целом) можно охарактеризовать так: математики в своих исследованиях полагаются на эмпирическое знание физиков, а физики полагаются на обоснованность выводов математики. В результате мы имеем некое знание, в котором полно нестыковок и парадоксов. Вначале рассмотрим математические парадоксы.
Известно, что дивергенция потенциального электрического поля вне источников и стоков всюду признается равной нулю. Ротор потенциального поля тоже всюду равен нулю. Сказанным характеризуют электрическое поле и на границе раздела диэлектрических сред, при этом равенство нулю дивергенции вектора электрической индукции D и равенство нулю циркуляции вектора напряженности электрического поля Е чаще всего принимают в качестве граничных условий.
На рис.1 приведено традиционное изображение поведения векторов D и Е на границе двух диэлектрических сред. Равные проекции векторов D и Е на координатные оси помечены особыми значками.
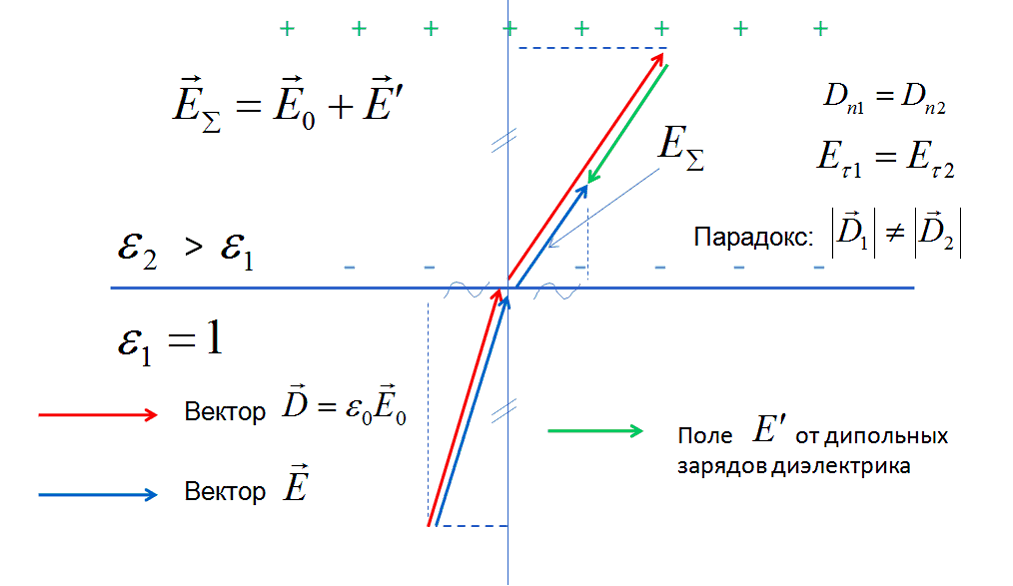
Рис.1. Поведение электрических векторов на плоской границе двух сред в традиционном представлении
Отметим первый парадокс. Рис.1 со всей очевидностью показывает, что вектор D в диэлектрике с большей диэлектрической проницаемостью ![]() обязательно будет увеличенным по модулю. Это свойство вектора D подтверждают и многочисленные источники.
обязательно будет увеличенным по модулю. Это свойство вектора D подтверждают и многочисленные источники.
Увеличение модуля вектора означает, по мнению автора [4], наличие ненулевого значения дивергенции. По рис.1 это место расположения точки преломления вектора, но по современным представлениям этого быть не должно по причине отсутствия на границе двух сред свободных электрических зарядов. Последнее можно подтвердить математически.
Если горизонтальную линию рис.1 принять за ось х, а вертикальную линию за ось у, то при разной длине вектора D в верхней и нижней частях изображения, сумма частных производных ![]() не будет равна нулю. Если бы преломление вектора D происходило без изменения его длины (другими словами, наблюдался бы поворот вектора), то сумма частных производных, входящих в определение дивергенции, была бы нулевой. Приращение одной проекции вектора компенсировалось бы уменьшением другой проекции. Но так вопрос не ставится и обсуждать этот вариант нет необходимости.
не будет равна нулю. Если бы преломление вектора D происходило без изменения его длины (другими словами, наблюдался бы поворот вектора), то сумма частных производных, входящих в определение дивергенции, была бы нулевой. Приращение одной проекции вектора компенсировалось бы уменьшением другой проекции. Но так вопрос не ставится и обсуждать этот вариант нет необходимости.
Второй парадокс модели поведения электрических векторов по рис.1 заключается в том, что на границе двух диэлектрических сред в точке преломления векторов D и Е получается ненулевое значении ротора, что совершенно неизбежно при любом изменении направления вектора, но совершенно исключено для потенциального поля. Поясним это подробнее.
Утверждение о непрерывности тангенциальных (касательных) составляющих напряженности потенциального электрического поля считается верным применительно к любой произвольной поверхности и в любой ее точке [3, стр.42]. Однако границу двух сред нельзя считать произвольно выбранной поверхностью. Это особая поверхность с образованием на ней под воздействием внешнего поля связанных электрических зарядов с превалированием заряда одного определенного знака (поэтому и происходит скачок нормальной составляющей вектора напряженности поля).
Линии напряженности электрического поля, подходящие под углом от нормали к поверхности раздела двух сред, обязательно претерпевают изломы, а это означает, что в точках излома линий вектора Е ротор этого вектора не будет равен нулю. Последнее означает, что электрическое поле на границе раздела двух сред по определению нельзя считать потенциальным (![]() ). Ну, а если поле на границе двух сред не потенциальное, то требование равенства тангенциальных составляющих вектора Е на этой границе совершенно необоснованно. Покажем это математически.
). Ну, а если поле на границе двух сред не потенциальное, то требование равенства тангенциальных составляющих вектора Е на этой границе совершенно необоснованно. Покажем это математически.
Если, как и в предыдущем рассмотрении, принять горизонтальную линию рис.1 за ось х, а вертикальную линию за ось у, то ось z будет расположена перпендикулярно плоскости рисунка. При этом составляющие векторов ![]() и частные производные этих составляющих по направлениям осей х и у тоже равны нулю. Анализируя общую формулу выражения ротора для вектора Е:
и частные производные этих составляющих по направлениям осей х и у тоже равны нулю. Анализируя общую формулу выражения ротора для вектора Е:
получим
Последнее выражение при неизменных составляющих вектора напряженности электрического поля по оси х (![]() ) будет равно
) будет равно ![]() . Из-за скачка нормальной составляющей напряженности электрического поля на границе двух сред данная производная оказывается бесконечно большой по величине и конкретно не определенной. Единственно, что можно сказать о функции
. Из-за скачка нормальной составляющей напряженности электрического поля на границе двух сред данная производная оказывается бесконечно большой по величине и конкретно не определенной. Единственно, что можно сказать о функции ![]() - она не равна нулю, а значит электрическое поле на линии (в трехмерном изображении – на поверхности) преломления вектора Е, не потенциальное.
- она не равна нулю, а значит электрическое поле на линии (в трехмерном изображении – на поверхности) преломления вектора Е, не потенциальное.
Еще одним недостатком модели поведения векторов по рис.1 является слишком упрощенное представление, в котором не показывается влияние на поворот вектора Е составляющей напряженности поля от пограничной разности потенциалов. Такое влияние безусловно есть и, как далее показывается, для поворота вектора Е оно определяющее.
В дополнение к изложенному доводу можно привести парадоксальные изображения поля вектора D в классических примерах с диэлектрическим и проводящим шаром [5]. На рис.2 а) приведен пример Зоммерфельда с диэлектрическим шаром, на рис.2 б) приведен другой его пример с проводящим шаром. В том и другом случае вещественные образования играют роль своеобразного «ферроэлектрика», стягивающего в себя и сгущающего линии внешнего однородного поля. Однако «ферроэлектриков» в природе нет.
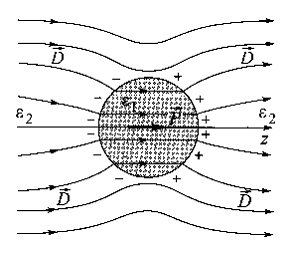 а)
а) 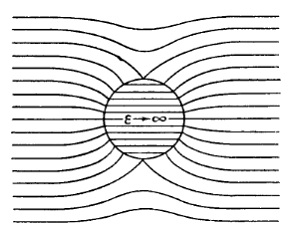 б)
б)Рис. 2. Изображение (по Зоммерфельду) деформаций однородного поля D диэлектрическим – а) и проводящим – б) шарами
Ясно, что на поверхности того и другого шара для линий поля D испытывают, как показано на рисунках, изломы, означающие преломление в этих местах вектора D. В местах изломов пространственные производные не могут быть равны нулю. Вследствие этого ротор вектора D на шаровой пограничной поверхности не может быть равным нулю. Все это означает, что поле D на указанных поверхностях, естественно и поле Е, не могут считаться потенциальными. Отсюда следует главный для нас вывод, который мы будем использовать в дальнейших рассуждениях: касательные составляющие вектора Е по обе стороны от границы раздела двух диэлектрических сред имеют право быть неравными друг другу.
Естественно, что наш последний вывод противоречит современным представлениям о граничных условиях для электростатического поля, но не надо бояться своих собственных выводов (завещание Маркса). Посмотрим критически на обоснование Зоммерфельда приводимых изображений. Математическое обоснование этих изображений дается Зоммерфельдом с использованием функций Грина и привлечением метода анализа электрического поля в зеркальном сферическом отображении. Соответствие этих изощренных математических методов физической реальности представляется автору весьма сомнительным. Получаемое сгущение линий поля внутри шаров физически означает усиление поля, но из опыта известно, что в диэлектриках внешнее электрическое поле только ослабляется.
Указанные парадоксы математической теории поля почему-то не замечаются и не анализируются. В «официальной» физике эти проблемы тоже не принято их обсуждать. Частичное подтверждение авторской позиции удалось обнаружить в работе [6, стр.38], цитируем.
«До сих пор предполагалось (примеч., в их книге), что ![]() ,
, ![]() и
и ![]() являются произвольными функциями
являются произвольными функциями ![]() и r. Однако, как правило, они оказываются кусочно-непрерывными функциями координат, т.е. претерпевают разрывы на некоторых границах раздела. Обусловлено это тем, что применяемые на практике технические устройства включают в себя элементы, обладающие различными
и r. Однако, как правило, они оказываются кусочно-непрерывными функциями координат, т.е. претерпевают разрывы на некоторых границах раздела. Обусловлено это тем, что применяемые на практике технические устройства включают в себя элементы, обладающие различными ![]() ,
, ![]() и
и ![]() .
.
В связи с этим можно получить решение уравнений Максвелла лишь в отдельных областях пространства, где коэффициенты ![]() ,
, ![]() и
и ![]() непрерывны. Полученное таким образом общее решение системы дифференциальных уравнений содержит некоторые произвольные функции. Чтобы их определить и получить решение для всей совокупности областей, необходимо наложить граничные условия, или, как говорят, «сшить» решения на границах областей.
непрерывны. Полученное таким образом общее решение системы дифференциальных уравнений содержит некоторые произвольные функции. Чтобы их определить и получить решение для всей совокупности областей, необходимо наложить граничные условия, или, как говорят, «сшить» решения на границах областей.
Эти условия «сшивания», налагаемые на векторы E, D, B, H легко вывести, используя интегральную форму уравнений Максвелла (10.4). В самом деле, применять в пограничной области уравнения в дифференциальной форме нельзя, так как поля на границе могут терпеть разрывы, поэтому пространственные производные от них могут не существовать. Однако уравнения в интегральной форме, безусловно, должны выполняться, так как они являются непосредственным следствием экспериментальных фактов».
По изложенному тексту работы [6] можно сделать разные выводы. Первый вывод – о несоответствии друг другу уравнений Максвелла, выраженных в дифференциальной и интегральной формах. Второй вывод – экспериментальные факты «притянуты за уши» для разрешения трудностей математики. Третий вывод – наши представления о граничных условиях для электромагнитных векторов не верны.
Автор настоящей статьи видит разрешение большинства обозначенных выше парадоксов в восприятии по-новому вектора D: не составным и вспомогательным, как это трактуется в современных вузовских учебниках по электромагнетизму [1-2], а по-иному. Вектор D видится автору вакуумной составляющей электрического поля, которая в однородном поле неизменна как вне, так и внутри диэлектрика. Эта составляющая (вектор D) внутри диэлектрика вызывает появление вещественной составляющей электрического поля (вектор Р). Очень важно понимать, что эти две суперпозиционные составляющие (векторы D и Р) независимы друг от друга. Результатом суперпозиции (линейного наложения) полей векторов D и Р получается поле вектора Е, которым привыкли чаще всего оперировать. Для согласования разнородных размерностей, по сути, вещественных векторов D и Р с полевым вектором Е в системе СИ используется электрическая постоянная ![]() . Кроме нее в согласовании размера электрических величин Е и D внутри диэлектрика (без участия Р) используют безразмерную диэлектрическую проницаемость
. Кроме нее в согласовании размера электрических величин Е и D внутри диэлектрика (без участия Р) используют безразмерную диэлектрическую проницаемость ![]() , ранее совершенно правильно именовавшуюся относительной электрической проницаемостью (относительно вакуума).
, ранее совершенно правильно именовавшуюся относительной электрической проницаемостью (относительно вакуума).
Приводимые далее модельные изображения электрических линий и векторов внутри и на границе диэлектрических сред основаны на авторском представлении о физической сущности поляэлектрической индукции D (по иному, электрического смещения) как поляризованности вакуума. Это понятие введено давно [7, стр.64] его происхождение в современной физике объясняется наличием виртуальных частиц физического вакуума, поэтому возражений вызывать не должно. Поляризованность вакуума модельно представляется в виде объемной плотности суммарногоэлектрического дипольного момента, создаваемого виртуальными частицами вакуума. Виртуальные частицы, как известно, возникают парами (частица плюс античастица, образуя электрический диполь) в любой точке пространства (как внутри веществ, так и в вакууме) и существуют весьма короткое время в соответствии с соотношением неопределенностей Гейзенберга. В сильных электрических полях виртуальные частицы способны превращаться в реальные микрочастицы [8, стр. 107; 9].
Удивительно, но по современным представлениям виртуальные частицы возникают и существуют (положенное им время) не только в пустоте вакуума или, так сказать, в «пустотах» вещества, но и внутри самих атомов, «пустота» которых тоже общеизвестна, а сильнейшие электрические поля присутствуют как раз там.
Как уже отмечалось выше, суммарное поле двух поляризованностей, образуемое по принципу суперпозиции, и есть то, что мы обычно называем электрическим полем. Математически это соотношение можно выразить так:
Однако общепринято представлять электрическое поле не как поле суммарной поляризованности вакуума и вещества, а в виде поля вектора электрической напряженности Е:
В приводимых формулах вектор Р обозначен значком (*) ввиду того, что привычный вектор поляризованности не совсем удачно принят противоположно направленным среднему электрическому полю, создаваемому дипольной парой зарядов. В реальности поле вектора Р (если так можно выразиться) имеет сложный дипольный вид, оно изменчиво по величине и направленности, что будет показано чуть ниже.
Думается, что вектор Е в свое время (исторически) ввели как простой силовой вектор. Действительно, он прост и удобен. Но этот вектор не учитывает присутствия вездесущей диэлектрической среды – вакуума, о свойствах которого (эфир-вакуум, кипящий виртуальными частицами) в то время не знали. Поэтому вполне возможно, что в будущем электромагнитные векторы Е и B будут признаны фантомными [10].
Отметим, что с помощью вектора D и подобного ему вещественного вектора Р можно описывать все электрические процессы и явления, в том числе и волновые [11]. Возможно, такое описание менее удобно, чем привычное описание с использованием вектора Е, но это не самое важное при рассмотрении физической сущности электрических явлений. Постижение истинного положения вещей ценнее удобства описания.
С учетом изложенных представлений, автор по-своему видит картину линий электрического поля внутри и вблизи диэлектрика (рис.3) и картину поведения электрических векторов на границе двух диэлектрических сред (рис.4).
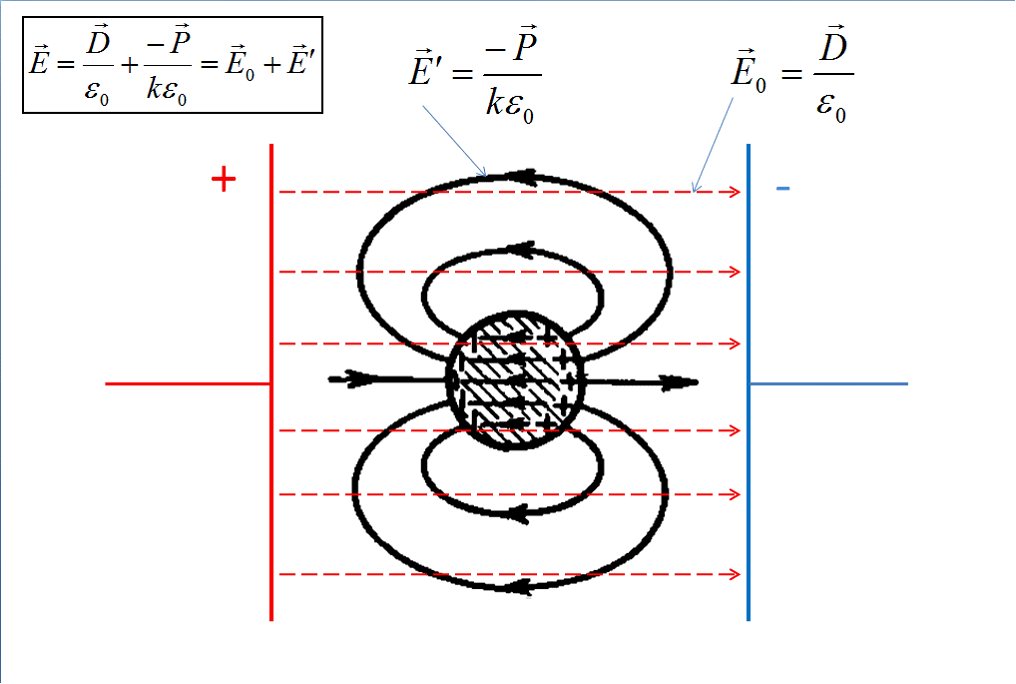
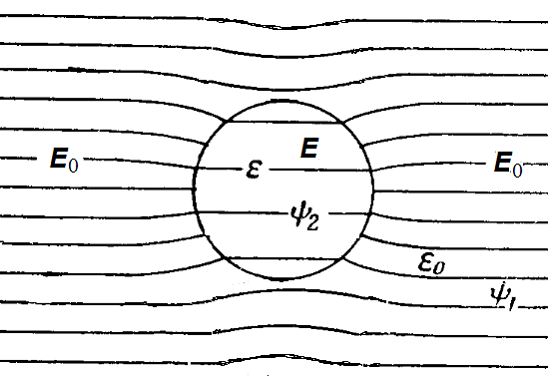
Рис.3. Составляющие а) и результат суперпозиции б) двух полей.
Электрическое поле (вне и внутри) диэлектрического шара, помещенного во внешнее однородное электрическое поле, должно представлять собой суперпозицию двух полей: первичного однородного поля и вторичного дипольного поля, создаваемого шаром. Первичное однородное поле ![]() рис.3 а) создается плоским конденсатором, а вторичное дипольное поле
рис.3 а) создается плоским конденсатором, а вторичное дипольное поле ![]() диэлектрического шара имеет дипольный вид. Внутри однородно поляризованного шара значение k в формуле для
диэлектрического шара имеет дипольный вид. Внутри однородно поляризованного шара значение k в формуле для ![]() равно трем [1, стр.91] при условии эквивалентности поля шара полю диполя, имеющего электрический дипольный момент величиной Р. Однако вне шара значение k будет зависеть от расположения точек, в которых рассматривается поле. Наглядная картина суперпозиции двух рассматриваемых полей изображена на рис.3 б).
равно трем [1, стр.91] при условии эквивалентности поля шара полю диполя, имеющего электрический дипольный момент величиной Р. Однако вне шара значение k будет зависеть от расположения точек, в которых рассматривается поле. Наглядная картина суперпозиции двух рассматриваемых полей изображена на рис.3 б).
Данная картина может быть рассчитана математически путем наложения однородного векторного поля ![]() и дипольного поля, описываемого с помощью радиальной и угловой составляющих [1, стр.34]:
и дипольного поля, описываемого с помощью радиальной и угловой составляющих [1, стр.34]:
Как видим, применение простого, но методологически безупречного принципа суперпозиции, избавляет нас от необходимости использования изощренных математических методов, применявшихся Зоммерфельдом. При этом результат получается явно более правдоподобный.
Теперь применим метод суперпозиции и обратный ему метод почленного разложения к рассмотрению поведения электрических векторов D и Е на границе двух сред (рис.4).
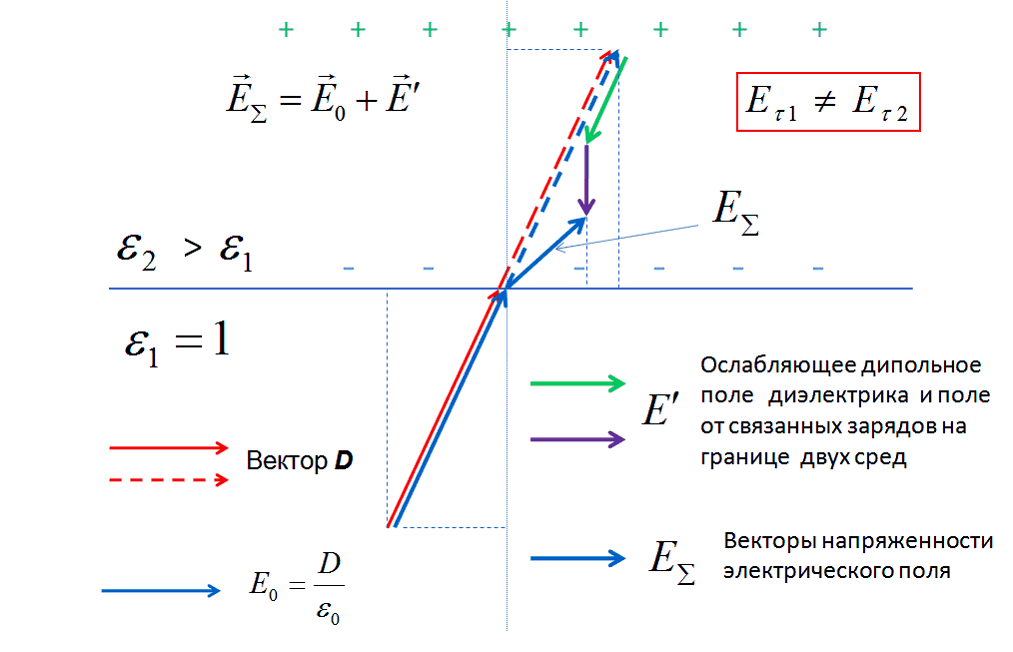 Рис.4. Модель реального поведения электрических векторов на границе двух сред.
Рис.4. Модель реального поведения электрических векторов на границе двух сред.По модели рис.4 вектор D (по масштабу он принят равным Е0) вообще не испытывает преломления, то есть он как бы «не чувствует» среду. Нормальная и касательная составляющие вектора D при переходе через границу двух сред остаются неизменными. Результирующее электрическое поле образуется в каждой точке пространства как векторная сумма первичного поля поляризованностивакуума и вторичного поля поляризованности диэлектрической среды. То есть выполняется всеобщий и методологически верный принцип суперпозиции. Для перехода от размерностей векторов D иР к обозначенным на рис.4 составляющим вектора Е требуется лишь их деление на размерность электрической постоянной ![]() .
.
Вектор Е, входящий в диэлектрическую среду параллельно вектору D под тем же углом к нормали, как и любой вектор данного типа, испытывает преломление с поворотом от нормали к поверхности раздела двух сред. Рис.4 показывает, что поворот вектора Е обусловлен не ослабляющим действием диэлектрика, а наличием связанных зарядов на поверхности раздела двух сред и конфигурацией этой поверхности. Наличие данной составляющей реакции среды объясняет характер поведения световых лучей на границе двух диэлектрических сред. Конфигурация граничных поверхностей при участии показателей преломления двух сред определяет закон преломления световых лучей и их расположение в одной плоскости с нормалью к поверхности раздела сред. Преломленный луч обычнотоже расположен в этой же плоскости. (В кристаллах возможны необыкновенные лучи, которые после преломления не лежат в одной плоскости с падающим лучом и нормалью к преломляющей поверхности).
Изображение результирующего вектора напряженности электрического поля ![]() внутри диэлектрика в виде трех составляющих:
внутри диэлектрика в виде трех составляющих: ![]() - от первичной поляризованности вакуума и двух составляющих реакции диэлектрика на внешнее поле (на рис.4
- от первичной поляризованности вакуума и двух составляющих реакции диэлектрика на внешнее поле (на рис.4 ![]() имеет две составляющие) соответствует принципу суперпозиции. Поэтому изображение рис.4 в дополнение к изображениям рис.3, служит наглядным подтверждением верности авторских представлений о поведении электрических векторов на границе двух сред, какими бы странными эти представления сегодня ни казались.
имеет две составляющие) соответствует принципу суперпозиции. Поэтому изображение рис.4 в дополнение к изображениям рис.3, служит наглядным подтверждением верности авторских представлений о поведении электрических векторов на границе двух сред, какими бы странными эти представления сегодня ни казались.
Иногда автору предлагают привести наглядный пример потенциального поля, в котором циркуляция вектора Е по замкнутому контуру была бы не равна нулю. Такой пример имеется, он приведен на рис.5. В работе [12] приводится расчет напряженностей электрического поля в таком конденсаторе в свободном пространстве и в диэлектрике.
Если конденсатор имеет квадратные пластины площадью S и заряжен до напряжения U, то напряжения на конденсаторах (с учетом формул рис.5) определятся выражениями:
![]()
![]()
![]() .
.
Напряженности электрического поля в конденсаторах эквивалентной схемы рис.5 определятся выражениями:
Здесь ![]() - диэлектрическая проницаемость диэлектрика.
- диэлектрическая проницаемость диэлектрика.
Как видим в этом примере, на границе двух сред ![]() . Интересно, что такой же результат получается и на боковой границе конденсаторов С1 и С2.
. Интересно, что такой же результат получается и на боковой границе конденсаторов С1 и С2.
Этот пример показывает, что циркуляция вектора Е может быть не равной нулю не только на границе двух сред, но и в свободном от вещества пространстве. Парадоксально, но факт! Этот расчет легко проверяем на опыте.
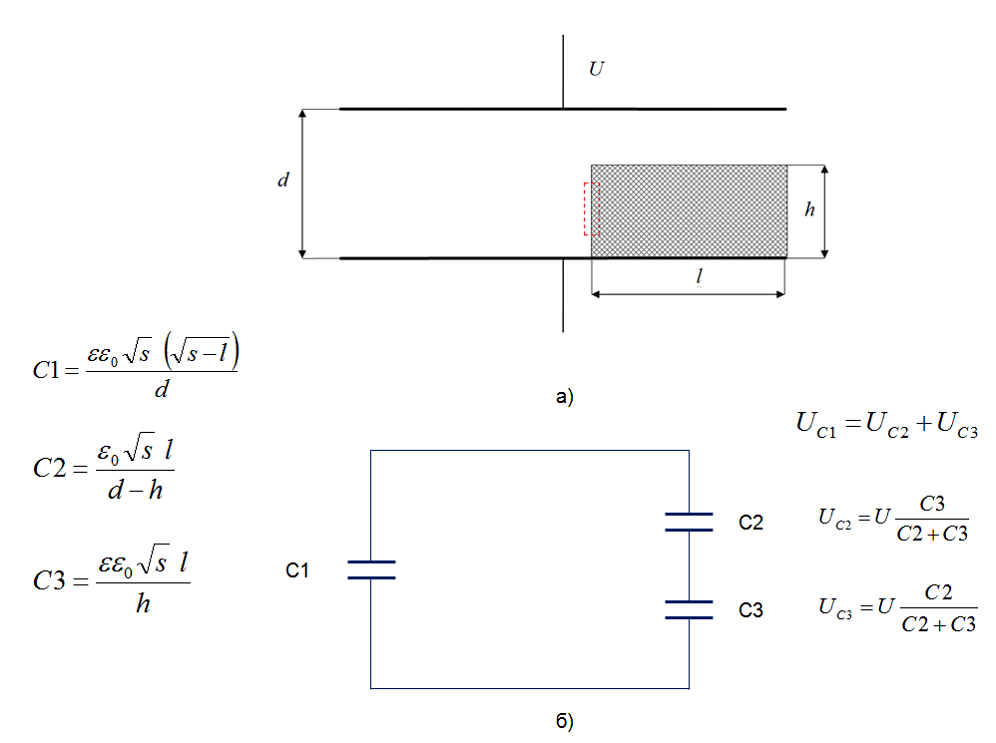
Рис.5. Пример устройства, в котором на границе двух сред
Согласно принципу фальсифицируемости, одного эмпирического факта достаточно, чтобы опровергнуть существующую научную теорию. Такой факт, опровергающий существующую теорию граничных условий в электростатике – выявился (см. рис.5), поэтому вполне оправдана будет постановка вопроса о необходимости доработки этой теории, какой бы привычной и надежной эта теория нам сегодня ни казалась.
Спрашивается, чем же можно заменить известную теорию о равенстве касательных составляющих вектора Е на границе двух сред? Автор статьи видит ответ на этот вопрос в формировании нового представления о неизменности вектора D на границе двух сред и использовании в качестве граничных условий равенства нормальных и касательных составляющих этого вектора по обе стороны от границы двух сред.
О том, что с теорией граничных условий в электростатике не все в порядке сигнализирует и несовпадение формул, определяющих соотношение углов падения и преломления световых лучей (закон Снеллиуса) и традиционное соотношение углов падения и преломления векторов D и Е на границе двух сред. А ведь направление распространения светового луча и направление колебаний вектораЕ в этом луче должны быть строго перпендикулярны.
Картина, поясняющая сказанное, изображена на рис.6.
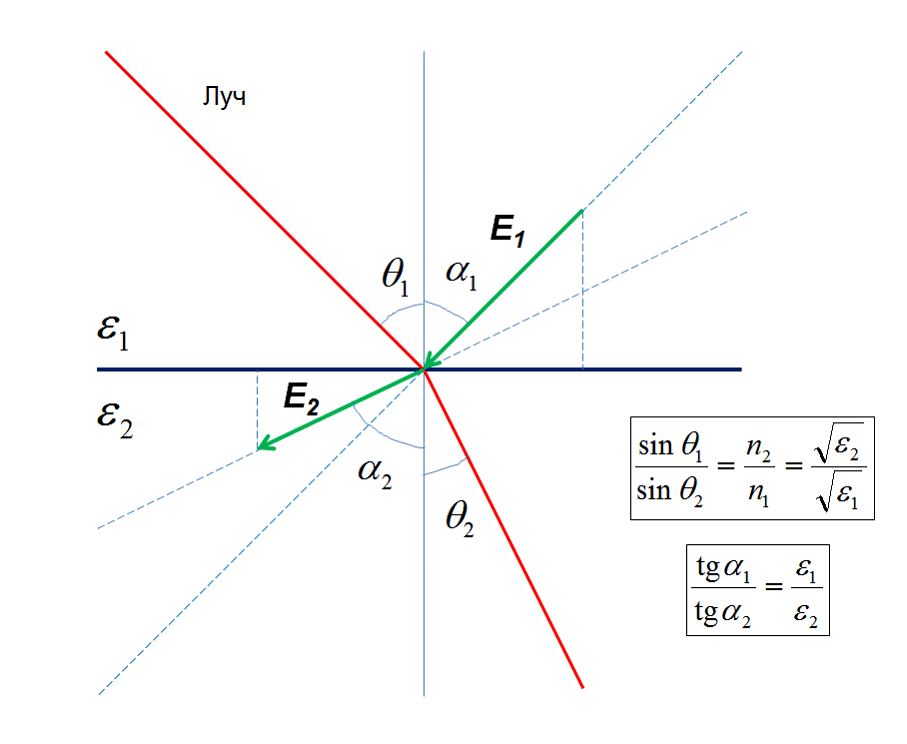 Рис.6. Соотношения для углов преломления светового луча и вектора Е на границе двух сред.
Рис.6. Соотношения для углов преломления светового луча и вектора Е на границе двух сред.
Для справки, закон Снеллиуса, связывающий угол падения с углом преломления световых лучей, выражается соотношением:
 .
.До сих пор используемое соотношение аналогичных углов от нормали для векторов Е и D иное:
Очевидные соотношения для самих углов: ![]() и
и ![]() . Поскольку углы
. Поскольку углы ![]() и
и ![]() связаны через прямой угол
связаны через прямой угол ![]() , то какое-то одно из представленных соотношений углов не верно.
, то какое-то одно из представленных соотношений углов не верно.
Если принять верными оба соотношения, то придется признать, что вектор Е не перпендикулярен направлению распространения луча. Если не сомневаться в последнем, то следует признать неверным одно из двух соотношений. Как говорится, третьего не дано.
Как можно понять из всего изложенного, автор ставит под сомнение достоверность широко используемого «закона» преломления электрических векторов. В поддержку авторской точки зрения можно привести то, что оптические законы более просты, наглядны, сравнительно лучше изучены и их достоверность почти несомненна. Сомневаться в ортогональности вектора Е направлению распространения электромагнитной волны или светового луча тоже нет оснований.
Выводы.
1. Рассмотрен ряд парадоксов существующей теории электрического поля и показано несоответствие широко используемых граничных условий требованиям потенциальности поля и принципу суперпозиции. Основание к такому заключению – на границе двух сред дифференциальные выражения дивергенции и ротора вектора напряженности поля не равны нулю и наблюдаемая реальность соответствует данным математическим операциям.
2. Для разрешения существующих парадоксов предложена новая модель поведения электрических векторов на границе двух сред, согласно которой откорректировано и приближено к реальности известное изображение поля внутри и вблизи шаровых тел.
3. Предложенные модели соответствуют принципу суперпозиции, методологически верному и всеобщему. Поэтому эти модели имеют основание претендовать на их адекватность физической реальности.
Библиографический список
- О граничных условиях ЧуевО граничных условиях Чуев1. Иродов И.Е. Электромагнетизм. Основные законы. Изд. 4-е испр.– М.: БИНОМ. Лаборатория знаний. 2003. – 320 с.
- Савельев И.В. Курс общей физики: В 5 кн.: Кн. 2: Электричество и магнетизм: Учеб. Пособие для втузов. – М.: «Издат. АСТ». 2004. -334 с.
- Тамм И.Е. Основы теории электричества. Учеб. пособие для вузов. – 11-е изд., испр. и доп. – М.: ФИЗМАТЛИТ, 2003. – 616 с.
- Чуев А.С. О понятии дивергенции поля векторных физических величин // Современные научные исследования и инновации. 2013. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2013/01/20234 (дата обращения: 31.07.2014).
- Зоммерфельд А. Электродинамика. Перевод с нем. – М.: Издат. Иностр. Литер. 1958. – 505 с.
- Терлецкий Я.П., Рыбаков Ю.П. Электродинамика. – М.: Высшая школа. 1990. – 352 с.
- Поляризация вакуума. Физическая энциклопедия. Главный редактор А.М. Прохоров. – М.: Советская энциклопедия. 1988, 690 с.
- Малая Советская Энциклопедия, том.2, третье издание, 1958, Гос. науч. издат. «БСЭ».
- Смолянский С.А. Вакуумное рождение частиц в сильных электромагнитных полях. // Соросовский образовательный журнал, 2001, № 2, с. 69-75.
- Чуев А.С. Полевые электромагнитные величины – фантом или реальность?// «Законодательная и прикладная метрология». 2012. №3. С. 71-75.
- Чуев А.С. Описание электромагнитных волн в вакууме с использованием физических величин поляризованность и намагниченность. // Наука и образование. Электрон. Изд. МГТУ им. Н.Э. Баумана. 2012, №6. Режим доступа: http://technomag.edu.ru/doc/425164.html. (Дата обращения: 6.06.2012 г.).
- Можаев В. Диэлектрики в электрическом поле. // Журн. «Квант». №3. 2006. С. 39-42.
