Сокращение запасов природного топлива ведет к развитию любой ЭЭС при все большем использовании возобновляемых энергоресурсов, таких как ветровая или солнечная энергия, которые во многих странах составляют большую часть распределенной генерации. Таким образом их развитие, управление, защита и использование являются основными задачами на сегодня. В данной публикации рассмотрим на примере ОЭС Украины, как разработать регулятор для управления подключением рассредоточенной генерации.
Представляем всю ОЭС как совокупность генераторов определенной мощности, данные по мощностям были представлены для использования представителями НЭК «Укрэнерго», в сумме на конец 2013года генерация составляет 54504,4 МВт. [1] и представлена в виде 52 генераторов, главный расчетный параметр, который имеем – зависимость частоты напряжения на выходе генераторов от времени после подключения мощного потребителя и дефицита мощности в системе. Графики этой зависимости изображены на рис. 1.

Разбивать группу генераторов на два кластера будем используя ПО для статистических расчетов StatSoft “Statistica 6.0″.
При работе с программой «Statistica 6.0» применялись различные сочетания правил объединения объектов при формировании кластеров (одиночный связь или метод ближайшего соседа, полных связей или метод наиболее удаленных соседей, невзвешенный и взвешенный попарного среднего, невзвешенный и взвешенный центроидного, Варда) и метрик расстояния между объектами в многомерном пространстве признаков (евклидова, квадратичная евклидова, Манхэттенский расстояние, расстояние Чебышева). В общей сложности было реализовано 17 вариантов кластеризации генераторов. Самым устойчивым оказалось разбиение объектов на два кластера, каждый из которых включает более одного объекта. Из них наиболее часто встречается вариант кластеризации, приведен ниже:
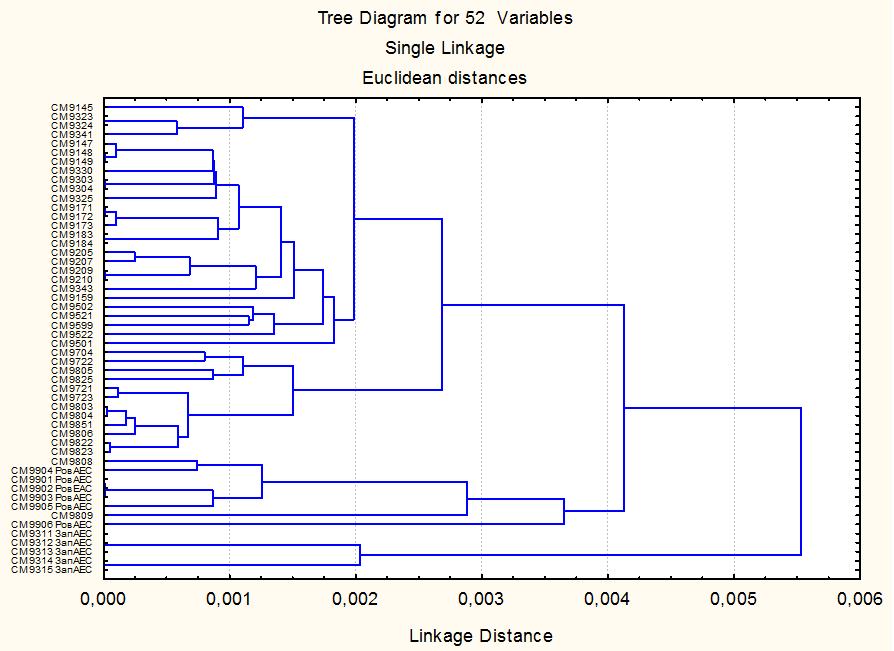
Первый кластер: СМ 9145, СМ 9147, СМ 9148, СМ 9149, СМ 9159, СМ 9171, СМ 9172, СМ 9173, СМ 9183, СМ 9184, СМ 9205, СМ 9207, СМ 9209, СМ 9210, СМ 9303, СМ 9304, СМ 9311 ЗапАЕС, СМ 9312 ЗапАЕС, СМ 9313 ЗапАЕС, СМ 9314 ЗапАЕС, СМ 9315 ЗапАЕС, СМ 9323, СМ 9324, СМ 9325, СМ 9330, СМ 9341, СМ 9343, СМ 9501, СМ 9502, СМ 9521, СМ 9522, СМ 9599.
Второй кластер: СМ 9316 ЗапАЕС, СМ 9704, СМ 9721, СМ 9722, СМ 9723, СМ 9803, СМ 9804, СМ 9805, СМ 9806, СМ 9808, СМ 9809, СМ 9822, СМ 9823, СМ 9825, СМ 9851, СМ 9901 РовАЕС, СМ 9902 РовЕАС, СМ 9903 РовАЕС, СМ 9904 РовАЕС, СМ 9905 РовАЕС, СМ 9906 РовАЕС.
Дендрограмма одного из вариантов кластеризации приведена на рис. 2. По оси абсцисс показаны объекты кластеризации (регионы), по оси ординат-значение расстояний, при которых происходит последовательное объединение объектов.
На втором этапе было реализовано итерационный метод «k – средних» для числа кластеров k = 2. Кластеризация проведена за два итерации и изображена на рис. 3.

Таким образом мы получили две когерентные группы генераторов. Состав полученных кластеров полностью совпадает с методом при использованиии метода с дендограмой.
На следующем этапе выполняем проверку по «критерию ч2» [2], чтобы проверить удовлетворяют ли построенные графики кластеров условиям когерентности, что позволит нам перейти к следующему этапу – моделированию эквивалентной ОЭС. Критерий Хи-квадрат позволяет сравнивать распределение частот независимо от того, распределены они нормально или нет. Также преимущество этого критерия в том, что его можем применять для выборки объемом более 200 значений, в нашем случае n = 1000 значений.
Выберем количество интервалов: r = 40.
Вычислим ширину интервала:
Результаты измерений группируем по интервалам, вычисляем частоты mj значений xj, попадающих в j интервал. Рассчитанные данные для первого и второго кластеров заносим в таблицу 2.1 и таблицы 2.2 соответственно. Вычисляем среднее и выборочное СКО по формулам:
![]() (2)
(2)
Затем вычисляем значение:
Далее рассчитываем вероятность Pj, соответствующий j-му интервалу:
где
![]() – значение нормированной функции Лапласа.
– значение нормированной функции Лапласа.
Определяем критерий проверки:
На последнем этапе для избранное уровня значимости б из таблицы «Критические значения ![]() » [3] находят соответствующее значение
» [3] находят соответствующее значение ![]() для числа степеней свободы:
для числа степеней свободы:
где
l – количество параметров функции теоретического распределения.
Если ![]() , то разбиение генераторов на кластеры выполнены верно и можно переходить к этапу моделирования.
, то разбиение генераторов на кластеры выполнены верно и можно переходить к этапу моделирования.
Из результатов расчета для первого кластера 25,235 <53.393 и для второго кластера 44,456 <53.393 – разбиение выполнено верно. Расчетное значение критерия ч2 меньше табличного.
После того, как мы еквивалентировали ОЭС и разбили на кластеры, главной задачей является синтез регулятора, который управляет подключением ВИЭ для поддержания баланса мощностей в энергосистеме. Энергия ветра является одним из наиболее перспективных возобновляемых источников энергии через ее конкурентоспособную стоимость по сравнению с другими традиционными видами энергоресурсов. Ее производство безвредно для окружающей среды, и этот ресурс доступный в природе. Таким образом, энергия ветра может быть использована путем механического преобразования ее в электрическую энергию с помощью ветряной турбины. Будем рассматривать подключение мощных ветрогенераторов.
На рис. 4 показана принципиальная схема системы преобразования энергии ветра на основе синхронного генератора. Эта система непосредственно подключена к сети через систему преобразования энергии. Данная конфигурация системы называется «back-to-back PWM» [4] (спина к спине на основе широтно-импульсной модуляции) включена в сеть. Регулятор управляет углом поворота лопастей.

Рисунок 4 – Схема ветрогенератора с «back-to-back PWM» [5]
Генератором можно непосредственно управлять с генераторной стороны регулятором-1, в то время как со стороны сети регулятор-2 поддерживает напряжение на звене DC на желаемом значении с помощью экспорта активной мощности в энергосистему. Контроллер-2 также контролирует перетоки реактивной мощности с внешней сетью [6]. Итак, главная задача регулятора-1 это отслеживание максимальной возможной мощности ветрогенератора, а функция контроллера-2 – для контроля напряжения на звене DC и передача активной мощности в энергосистему.
Современный этап развития системного анализа и математического моделирования характеризуется расширением сферы их применения на слабо формализованные динамические системы. В большинстве случаев классические методы моделирования для таких систем не могут быть применены непосредственно, а следовательно, требуют определенной адаптации.
Математические модели динамических систем могут использоваться для анализа их динамики (имитации движения, прогнозирование будущих состояний) и оптимизации эволюции в будущем. В зависимости от цели моделирования может изменяться как сама модель, так и методы ее построения. Наиболее распространенными формами моделей динамических систем в математическом моделировании является дифференциальная или дифференциально-алгебраическая.
В системах управления, представлениям о пространстве состояний является математическая модель физической системы в виде набора входных и выходных переменных состояния, которые связаны дифференциальными уравнениями первого порядка. Чтобы отвлечься от количества входящих, выходящих параметров и состояния системы, переменные представляются в виде векторов. Кроме того, если динамическая система линейна и неизменна во времени, то дифференциальные и алгебраические уравнения можно записать в матричном виде. Представление о пространстве состояний (также известное как “time-domain approach”) обеспечивает удобный и компактный способ моделирования и анализа систем с несколькими входами и выходами. Имея р входов и q выходов, нам иначе пришлось бы записать q Ч p раз преобразование Лапласа для того, чтобы закодировать всю информацию о системе [7].
Главными элементами исследуемой ЕЭС являются генераторы, которые моделируют генерирующую мощности ОЭС.
Применительно к многомашинной ЕЭС система нелинейных дифференциальных уравнений трансформируется в систему нелинейных дифференциальных уравнений:
![]() (8)
(8)![]() [23]
[23]
где
![]() – отклонение углов поворота роторов от синхронно вращается декартовой системы координат i-го и j-го генераторов соответственно;
– отклонение углов поворота роторов от синхронно вращается декартовой системы координат i-го и j-го генераторов соответственно;
![]() – отклонение частоты i-го генератора от декартовой системы координат, которая синхронно вращается;
– отклонение частоты i-го генератора от декартовой системы координат, которая синхронно вращается;
![]() – постоянная инерции i-го генератора;
– постоянная инерции i-го генератора;
![]() – коэфициент демпфирования i-го генератора;
– коэфициент демпфирования i-го генератора;
![]() – ЭРС i-го и j-го генераторов соответственно;
– ЭРС i-го и j-го генераторов соответственно;
![]() – активная собственная проводимость узла i, к которому подключен i-й генератор
– активная собственная проводимость узла i, к которому подключен i-й генератор
Мощность, которая протекает в сеть в узле i и равна электрической мощности i-й синхронной машины, определяется как:
где
![]() – полная проводимость между i-м и j-м узлами;
– полная проводимость между i-м и j-м узлами;
![]() – аргумент полной комплексной проводимость между i-м и j-м узлами;
– аргумент полной комплексной проводимость между i-м и j-м узлами;
Необходимо отметить, что в момент, предшествующий переходному процессу (t=0), ![]() , то есть механическая мощность турбины i-го генератора:
, то есть механическая мощность турбины i-го генератора:
Индекс «0» означает исходное состояние ЭЭС и это относится к углам роторов всех синхронных машин и параметров сети, поскольку конфигурация сети в переходном режиме (после коммутаций) изменяется [8].
Наиболее распространенное представление пространства состояний линейной системы с р входами, q выходами и n переменными состояния записывается в следующем виде [9]:
![]()
![]() (11)
(11)
где
![]() – вектор состояний,
– вектор состояний, ![]() ;
;
![]() – выходной вектор,
– выходной вектор, ![]() ;
;
![]() – входной (управляющий) вектор,
– входной (управляющий) вектор, ![]() ;
;
![]() – матрица системы, dim[A] = nЧn;
– матрица системы, dim[A] = nЧn;
![]() – входная матрица, управляющая, dim[B] = nЧp;
– входная матрица, управляющая, dim[B] = nЧp;
![]() – выходная матрица, dim[C] = qЧn;
– выходная матрица, dim[C] = qЧn;
![]() – ведущая или прямой связи матрица (в случаях, когда модель системы не имеет прямой связи, то D – нулевая матрица), dim[D] = qЧp.
– ведущая или прямой связи матрица (в случаях, когда модель системы не имеет прямой связи, то D – нулевая матрица), dim[D] = qЧp.
Имеющие все необходимые данные и рассчитав необходимые коэффициенты системы можем выполнять моделирование регулятора в ПО MatLab “Simulink”.
Набор входных данных векторов:
A=[0 1 0 0; -6.098 -0.588 6.098 0;0 0 0 1;3.886 0 -3.886 -0.375];
B=[0 0 0 0;0 1 0 0;0 0 0 0;0 0 0 1];
C=[0 0 0 0;0 1 0 0;0 0 0 0;0 0 0 1];
D=[0 0 0 0;0 0 0 0;0 0 0 0;0 0 0 0];
Q=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
R=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
Расчетная блок схема имеет вид:

Рисунок 5 – Блок-схема для моделирования
В блоке State-Space1 с помощью уравнений состояния построили графики зависимости двух кластеров по угловой частоте, изображенные на рис. 6:

Рисунок 6 – Усредненный график двух кластеров
Как видим, они почти аналогичные тем, что мы получили с помощью кластерного анализа, а это означает, что модель системы достоверна. Во втором блоке State-Space2 реализован сам регулятор, где для управления используется обратная отрицательная связь. Его работу видим на рис. 7:

Рисунок 7 – Усредненный график двух кластеров после регулировки
Очевидно, что регулятор выполнил свою функцию, поскольку амплитуда по частоте значительно меньше и время затухания переходного процесса также намного меньше. Моделирование регулятора для ввода рассредоточенной генерации выполнено верно.
Библиографический список
- Изменение установленной мощности ОЭС Украины // Официальный интернет-портал «Укрэнерго». URL: http://www.ukrenergo.energy.gov.ua/ukrenergo/control/uk/publish/article?art_id=149524&cat_id=35061 (дата обращения: 05.06.2014)
- Циделко В. Д., Яремчук Н. О. Неопределенность измерений // Обработка данных и представление результата измерения. Политехника, 2002, с. 73-76.
- Аналитическая группа Статэксперт // Критические значения критерия χ2. URL: http://statexpert.org/articles/таблицы_критических_значений_статистических_критериев (дата обращения: 07.06.2014)
- Ali, M. E. Modelling of wind turbine driving permanent Magnet Generator with maximum power point tracking system. J. King Saud Univ., Riyadh, 2007 , 19(2), p. 223-237.
- Brendan, F, Damian, F, Leslie, B, Nick, J, David, M, Mark, O, Richard, W, & Olimpo, A. Wind power integration: connection and system operational aspects. Proc. IET Power and Energy Series, 2007, p. 50, 77-85.
- Ahmed, G. A, Dong-choon, L, & Jul-ki, S. Variable speed wind power generation system based on fuzzy logic control for maximum power output tracking. in Proc. 35 Annual IEEE Power Electron. Specialists Conf., PESC, Aachen, Germany, 2004 , 3, p. 2039-2043.
- Nise, Norman S. Control Systems Engineering (6th ed.). John Wiley & Sons, Inc., 2010, p. 34-35.
- Арнольд, В.И. Математические методы классической механики, М.: Физматгиз, 1974, c.121-123.
- Электронная энциклопедия Википедия // State space representation. URL: http://en.wikipedia.org/wiki/State_space_representation (дата обращения: 01.06.2014)
Количество просмотров публикации: Please wait