Введение
В первой части статьи разбирается известный «Парадокс близнецов» специальной теории относительности Эйнштейна (далее СТО). Показана несостоятельность объяснения этого парадокса с помощью общей теории относительности Эйнштейна (далее ОТО), а также наличие противоречий с часами в самой ОТО. Во второй части статьи приводится вывод преобразований электрического и магнитного полей, при которых уравнения электродинамики Максвелла, а также уравнение и величина силы Лоренца, являются инвариантными относительно преобразований координат Галилея. В третьей части статьи рассматривается сравнительное описание (с позиций теории относительности и классической механики Галилея-Ньютона) особенностей пространственного и спектрального распределения синхротронного излучения ультрарелятивистского электрона. Показано, что классическая механика вполне точно объясняет эти особенности несмотря на величину энергии электрона в этом явлении, которая с точки зрения теории относительности очень далеко выходит за пределы применимости классической механики. Для того, чтобы быть интересной для большего круга читателей, статья содержит минимальное количество математики, но при этом без ущерба для точности и доказательности. В статье везде, где это не оговорено особо, применяются следующие обозначения:
с – скорость света в СТО; γ – Лоренц-фактор в СТО.
Парадокс часов в теории относительности
Пожалуй, самый известный из всех парадоксов теории относительности это «Парадокс близнецов» или «Парадокс часов» СТО. Разъяснение этого парадокса еще в 1918 г. дал сам А. Эйнштейн в статье «Диалог по поводу возражений против теории относительности» [1 с. 616-625]. В этой работе описан следующий мысленный эксперимент. Пусть А и В – две удаленные друг от друга точки неподвижной системы К. Пусть U1 и U2 – двое совершенно одинаковых часов, расположенных в точке А и показывающих одинаковое время. Сообщим часам U2 некоторую постоянную скорость к точке В. Пусть в точке В скорость часов U2 меняется на противоположную и по возвращении в точку А они останавливаются. Так как наблюдаемое из К изменение показаний часов U2, произошедшее при их развороте, имеет некоторую конечную величину, и так как часы U2 при движении вдоль отрезка АВ идут медленнее часов U1, то при достаточно большой длине отрезка АВ часы U2 по возвращении в точку А должны отставать от часов U1 на некоторое время ∆t1. Если процесс перемещения часов U2 в точку В и обратно рассмотреть относительно системы К′, связанной с часами U2, в которой они неподвижны, то, учитывая неравноправность К и К′ в рамках СТО (вследствие неинерциальности К′), для расчета показаний часов U1 необходимо привлечение ОТО. В этом случае, как утверждается в вышеупомянутой статье, суммарное отставание часов U1 от U2 на участках постоянной скорости часов U1 относительно К′ на ∆t1 компенсируется их уходом вперед на ∆t2 во время разворота в гравитационном поле, возникающем в неинерциальной системе К′ на участке разворота, причем ∆t2 = 2∙∆t1. Таким образом, суммарно, как и в случае рассмотрения процесса относительно системы К, часы U2 будут отставать от U1 на ∆t1, т.е. никакого противоречия нет.
В своей статье Эйнштейн не приводит расчетов, но такой расчет можно найти в книге М. Борна «Эйнштейновская теория относительности» [2 с. 344-346]. В этих расчетах для вычисления опережения часов U1 по отношению к U2 на участке разворота в системе К′ используются следующие приближенные формулы [2 с.343, 345; 1 с.108-109, 597]:
τ1 ≈ τ2 /(1 – g∙L/c2) (1)
τ1 ≈ τ2 (1 + g∙L/c2) (2)
где:
τ1 – длительность разворота по часам U1;
τ2 – длительность разворота по часам U2;
g – напряженность гравитационного поля, возникающего при развороте часов U1 в системе К′ в соответствии с принципом эквивалентности ОТО;
L – длина отрезка АВ.
Формула (2) в дальнейшем приводит к нужному результату, а именно:
∆t2 = τ1 – τ2 ≈ τ2 ∙ g∙L/c2 ≈ 2∙∆t1 (3)
Но применение приближенных формул (1) и (2) может быть оправдано только при условии g∙L/c2 << 1, что означает L << c2/g, а одним из условий нашего мысленного эксперимента является достаточно большая длина L. Таким образом, мы не имеем права ограничивать длину отрезка АВ, напротив, должны допустить хоть и конечную, но сколь угодно большую величину L.
Чтобы у читателя не создалось впечатления, что условие L ≈ c2/g делает условия нашего мысленного эксперимента неправдоподобными с физической точки зрения, приведем простой расчет. Пусть ускорение, которое развивают двигатели часов U2, будет в 10 раз больше ускорения свободного падения на поверхности Земли g = 100 (м/с2), а скорость на участке равномерного движения в сто раз меньше скорости света V = 0,01∙c (м/с). Тогда время разгона часов U2 будет:
∆t = V/g ≈ 300 000 (с) ≈ 3,5 (дня).
Длина пути до разворота:
L = c2/g ≈ 9∙1014 (с) ≈ 0,095 (светового года).
Время в пути до разворота:
t ≈ L/V ≈ 9,5 (лет).
Получается вполне маленькое путешествие, не выходящее даже за пределы Солнечной системы (облако Оорта, считающееся границей Солнечной системы, находится от Солнца на расстоянии примерно 1 светового года).
Допустим, что для объяснения «Парадокса часов» СТО все же можно использовать приближенные формулы (1), (2) и (3). Тогда, если в системе К′ при развороте часов U1 в гравитационном поле их скорость меняется на 2∙V (от –V до V) за время τ2 по часам U2, для напряженности поля получаем:
g= 2∙V/τ2 (4)
C другой стороны, в системе К при развороте часов U2 их скорость также меняется на 2∙V, но за время τ1 по часам U1, поэтому ускорение часов U2 равно:
a= 2∙V/τ1 (5)
В соответствии с принципом эквивалентности ОТО напряженность гравитационного поля g в системе К′ равна ускорению aчасов U2 в системе К [1 с.562-563], поэтому, учитывая (4) и (5), получаем:
τ1= τ2
Этот результат совместим с уравнением (3) только в случае ∆t2 = ∆t1 = 0, т.е. когда часы U1 и U2 идут синхронно на всем протяжении путешествия часов U2.
Таким образом, ОТО не объясняет «Парадокса часов» СТО. Более того, как следует из изложенного выше, противоречия с часами свойственны также самой ОТО. Дополнительное подтверждение этому выводу дает следующий пример.
Пусть в системе отсчета К в точках А и В (отрезок АВ параллелен оси Х) находятся неподвижные синхронизированные часы, представляющие собой счетчики оборотов одинаковых идеальных маховиков МА и МВ. Гравитационное поле в К отсутствует. Маховики соединены тонкой эластичной невесомой нитью без проскальзывания. Нить натянута до предела, но т.к. маховики имеют одинаковые периоды обращения TA = TB и не вызывают дополнительного натяжения нити, она остается целой (рис. 1).
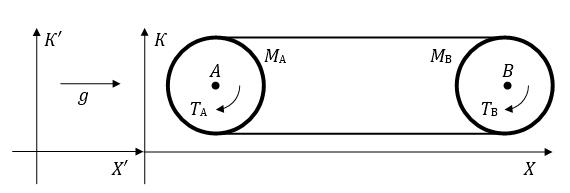
Рис. 1. Схема мысленного эксперимента с маховиками.
Перейдем в систему отсчета К′, движущуюся равноускорено относительно К в направлении, противоположном оси Х (оси Х и Х′ совпадают). В силу принципа эквивалентности ОТО в К′ существует гравитационное поле g, в котором часы свободно падают в направлении оси Х′. Пусть текущая мгновенная скорость системы К в К′ настолько мала, что эффектами СТО можно пренебречь (хотя это и не влияет на дальнейшие рассуждения). В системе К′ в точке А гравитационный потенциал выше, чем в точке В, поэтому часы в точке В идут медленнее. Это означает, что когда маховик МА делает полный оборот – маховик МВ еще нет. В результате на нижнем участке нити, наматывающемся на МА и разматывающемся с МВ, натяжение возрастает и она рвется. Порвется ли нить?
Инвариантность уравнений электродинамики
Общепринято полагать, что СТО устраняет проблему неинвариантности уравнений электродинамики Максвелла относительно преобразований Галилея. Вот, например, цитата из книги Р. Фейнмана [4 с.7]: «Однако уравнения Максвелла, по-видимому, не подчиняются принципу относительности: если преобразовать их подстановкой (15.2), то их вид не останется прежним» (подстановка (15.2) это преобразования координат Галилея).
Давайте внимательно разберемся с инвариантностью уравнений Максвелла. Инвариантность своих уравнений относительно преобразований Галилея анализировал уже сам Максвелл в «Трактате об электричестве и магнетизме». Этот раздел так и называется «Об изменении уравнений электродвижущей интенсивности в случае, когда оси, к которым они относятся, движутся в пространстве» [5 с. 467]. Вывод, который делает Максвелл, говорит сам за себя [5 с. 469]: «Отсюда вытекает, что электродвижущая интенсивность выражается формулой того же самого типа, будут ли движения проводников отнесены к неподвижным осям или к осям, движущимся в пространстве».
Нетрудно проверить, что приведенные ниже формулы преобразования полей оставляют форму уравнений Максвелла в штрихованной системе отсчета, движущейся скоростью V, неизменной относительно преобразований Галилея:
Е′ = E+ [V× B]/с
В′ = B
H′ = H– [V× D]/с
D′ = D
Кроме того, эти преобразования обеспечивают также инвариантность уравнения и величины для силы Лоренца относительно преобразований Галилея.
Форма материальных уравнений, связывающих напряженности и индукции полей, также остается неизменной. Причем наиболее просто они выглядят для неподвижных источников в вакууме, когда индукции прямо пропорциональны напряженностям, но в движущейся системе отсчета (как и при наличии среды в неподвижной системе) такая прямая пропорциональность исчезает, что связано с конечностью скорости распространения взаимодействий и их зависимостью от характера движения источников полей.
излучение ультрарелятивистского электрона
Доводы, приведенные в предыдущих разделах, дают основание предположить, что скорость света не является независящей от системы отсчета константой, а также что в природе нет ограничений на скорость движения материальных тел и справедливо Галилеево правило сложения скоростей. Наиболее показательными в этом смысле могли бы стать астрофизические явления, но имеющиеся наблюдательные астрофизические факты не позволяют с уверенностью сказать, какая из теорий (теория относительности или классическая механика) более точно описывает физическую реальность [11]. Поэтому, чтобы подчеркнуть сомнительность утверждения о том, что классическая механика является предельным случаем СТО для малых скоростей, рассмотрим в качестве примера синхротронное излучение ультрарелятивистского электрона.
Известно [6 с.27-28; 7 с.264], что синхротронное излучение направлено вдоль скорости электрона и сосредоточено в конусе с полным раствором, равным:
Δφ ≈ 2/γ
Причем для современных синхротронов γ >> 1. Объяснение этого феномена с точки зрения СТО – релятивистский поперечный эффект Доплера в совокупности с релятивистской аберрацией [6 с.27-28], которые заставляют электрон излучать преимущественно в направлении своего движения.
Посмотрим, что получится в рамках классической механики. В этом случае электрон движется по кольцу синхротрона с гиромагнитной частотой Ω, т.е. с частотой вращения электрона в магнитном поле, получающейся из условия равенства силы Лоренца FЛ = e∙VГ∙В/c и центростремительной силы FЦ = VГ∙Ω∙m0 при движении электрона по окружности:
Ω = e∙В/(m0∙c) = γ∙e∙В∙c/E= γ∙w0 (6)
где:
w0= e∙В∙c/E≈ с/R – циклотронная частота вращения электрона; в случае ультрарелятивистского электрона она равна отношению скорости света к радиусу орбиты электрона и не зависит от его энергии;
e, Е, m0 – заряд, энергия, масса покоя электрона;
В – индукция магнитного поля;
VГ= Ω∙R≈ γ∙c – линейная Галилеева скорость электрона.
Таким образом, электрон движется по кольцу синхротрона с линейной скоростью VГ (которая в γ раз больше скорости света). Пусть, для простоты, электрон излучает во все стороны равномерно. Скорость излучаемых им электромагнитных волн складывается по обычному Галилеевскому правилу с его собственной скоростью, поэтому для наблюдателя суммарное излучение как раз и будет сосредоточено в конусе с полным раствором Δφ ≈ 2/γ (рис. 2).
Рис. 2. Распределение излучения движущегося электрона.
На рис. 2 пунктирными стрелками условно показаны векторы излучения электромагнитных волн электроном относительно него самого со скоростью с. Сплошными стрелками показаны векторы скорости движения электрона относительно наблюдателя VГ. Штрихпунктирными стрелками показаны суммарные векторы скорости излучения относительно наблюдателя. Очевидно, что любой вектор суммарной скорости начинается в точке нахождения электрона и оканчивается на показанной пунктиром окружности.
Таким образом, «направленность» синхротронного излучения является прямым следствием Галилеевского правила сложения скоростей.
Рассмотрим далее еще одну особенность синхротронного излучения. Известно, что синхротронное излучение имеет максимум не на циклотронной частоте, а на ее очень высоких гармониках. Максимум излучения приходится на частоту, выражаемую соотношением [6 с.6; 7 с.265; 8 с.28-36]:
w ≈ w0(E/(m0∙c2))3 = w0∙γ3 (7)
где обозначения те же, что и в (6).
Возникает вопрос, почему излучение максимально не на циклотронной частоте, а на в γ3 раз большей? Приведем несколько качественных физических объяснений этого феномена в рамках СТО.
а) У Фейнмана [9 с.140] написано, что эффект вызван появлением «фактора сокращения», который связан с уменьшением масштаба времени. Но ведь время в системе отсчета, связанной с электроном, замедляется [1 с.597], т.е. наблюдаемая частота излучения должна уменьшиться, а не увеличиться.
б) Похожее объяснение есть в [6 с.32], где написано, что длительность импульса излучения в системе электрона τ′ связана с длительностью того же импульса в системе отсчета наблюдателя ∆t соотношением ∆t= τ′/γ2. Это соотношение означает, что импульс по часам наблюдателя более короткий, хотя согласно СТО должно быть наоборот (в системе наблюдателя часы идут быстрее).
в) Несколько иное объяснение дается в [8 с.28], цитата: «В лабораторной системе вследствие эффекта Доплера (частица движется на наблюдателя) принимается частота в γ2 раз больше». Однако в соответствии с формулой релятивистского эффекта Доплера [1 с. 78 формула (4а)], при движении электрона навстречу наблюдателю, и учитывая, что для ультрарелятивистского электрона V/c≈ 1, принимаемая частота должна быть следующей:
ν = ν0(1 + V/c) γ ≈ ν0∙2∙γ
Это означает, что вследствие релятивистского эффекта Доплера частота увеличивается не в γ2 раз, а в 2∙γ раз. Таким образом, все приведенные выше качественные физические объяснения соотношения (7) нельзя считать приемлемыми.
Посмотрим, что получится в рамках классической механики. В этом случае электрон движется по кольцу синхротрона с частотой Ω = γ∙w0. Принимая во внимание (как и в [6 с.32; 8 с.27]), что вследствие «прожекторного» эффекта электрон излучает в сторону наблюдателя только с короткого участка своей траектории, т.е. что интервал τ излучения электрона пропорционален отрезку дуги ∆φ = 2/γ, получаем:
τ = T/ (π∙γ) = 2/(γ∙Ω) (8)
где T – период обращения электрона по окружности синхротрона.
Для ультрарелятивистского электрона γ >> 1, поэтому τ << T. Это означает, что амплитуды гармоник такого импульса постоянны (как спектр дельта-импульса), т.е. практически не зависят от номеров гармоник [10 с.65-66], а т.к. энергия излучения зависит не только от амплитуды, но и от частоты, то мощность излучения будет расти по мере роста номера гармоники. Однако для такого импульса интервал спектра, содержащий подавляющую часть энергии импульса, не простирается до бесконечности, а ограничен соотношением [10 с.77]:
fc ≈ μ/τ (9)
где:
μ – число зависящее от формы импульса [10 с.77 таблица];
fc – граничная частота (в Герцах).
Таким образом, мощность излучения будет расти по мере увеличения частоты гармоники примерно до величины w′c = 2∙π∙fc, а потом начнет падать, т.е. максимум излучения должен быть на частоте w′c. Эта частота, в соответствии с соотношениями (8) и (9), равна:
w′c ≈ 2∙π∙μ/τ ≈ π∙μ∙γ∙Ω ≈ γ∙Ω
Учтем далее, что источник излучения (электрон) движется в сторону наблюдателя со скоростью VГ= γ∙c. При этом возникает (нерелятивистский) эффект Доплера (w/w′ = 1 + VГ/c= 1 + γ≈ γ), следовательно получаем увеличение наблюдаемых частот еще в γ раз. Частота, на которой наблюдается максимум излучения, увеличивается, соответственно, тоже в γ раз. Действительно, максимум излучения находится на верхней границе амплитудного спектра, которая так же, как и все частоты спектра, увеличивается в γ раз. Таким образом, для наблюдателя максимум излучения приходится на частоту:
wc= w′c∙γ= Ω∙γ2 = w0∙γ3 (10)
Соотношение (10) совпадает с (7). Получаем, что классическая механика вполне корректно описывает и спектральные, и пространственные особенности синхротронного излучения ультрарелятивистского электрона.
Библиографический список
- Эйнштейн А. Собрание научных трудов. В 4 т. Т.I. Работы по теории относительности 1905-1920; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1965. – 700 с.
- Борн М. Эйнштейновская теория относительности, перевод с английского Н.В. Мицкевича. – 2-е изд., испр. – М.: МИР, 1972. – 368 с.
- Эйнштейн А. Собрание научных трудов. В 4 т. Т.II. Работы по теории относительности 1921-1955; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1966. – 878 с.
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. В 9 т. Т.II. Пространство, время, движение. – М.: МИР, 1965. – 166 с.
- Максвелл Д.К. Избранные сочинения по теории электромагнитного поля, перевод З.А. Цейтлина под ред. П.С. Кудрявцева. – М.: Государственное издательство технико-теоретической литературы, 1952. – 687 с.
- Тернов И.М., Михайлин В.В. Синхротронное излучение. Теория и эксперимент. – М.: Энергоатомиздат, 1986. – 296 с.
- Ландау Л.Д., Лившиц Е.М. Теоретическая физика: Учеб. пособие. В 10 т. Т.II. Теория поля. – 7-е изд., испр. – М.: НАУКА, 1988. – 512 с. – ISBN 5-02-014420-7
- Байер В.Н., Катков В.М., Фадин В.С. Излучение релятивистских электронов. – М.: Атомиздат, 1973. – 376 с.
- Фейнман Р., Лейтон Р., Сэндс М.. Фейнмановские лекции по физике. В 9 т. Т.III. Излучение, волны, кванты. – М.: МИР, 1965. – 235 с.
- Харкевич А.А. Спектры и анализ. – 5-е изд. – М.: Книжный дом «ЛИБРОКОМ» 2009. – 240 с. – ISBN 978-5-397-00256-1
- Колесников, А.И., Лютый, В.М., Талызин, И.В. НАБЛЮДАТЕЛЬНЫЕ ФАКТЫ И ИХ ИНТЕРПРЕТАЦИЯ В АСТРОФИЗИКЕ. Вестник ТвГУ. Серия «Физика». 2005 г. №9(15). Выпуск 2. С. 124-131. ISSN 1995-0128 (http://eprints.tversu.ru/1244/)

