Одной из центральных проблем при разработке систем управления с нечеткой логикой остается синтез баз правил. Построение баз правил осуществляется с использованием экспериментальных данных, знаний и опыта экспертов или по результатам моделирования. К сожалению, для некоторых объектов управления экспериментальные данные получить сложно, а порой и невозможно. Эксперты не всегда могут охватить всю область допустимых изменений входных и выходных сигналов нечетких регуляторов, в результате чего база правил может не удовлетворять свойствам непрерывности, полноты и непротиворечивости. Построение баз правил по результатам моделирования эффективно, но здесь на передний план выходят жесткие требования к адекватности математической модели управляемого объекта.
Для решения проблемы генерации правил получили распространение методы интерполяции нечетких баз правил (fuzzy rule interpolation – FRI) [1], позволяющие по имеющейся априорной информации, синтезировать базу с указанными свойствами.
Аналогичной проблемой является синтез новой базы правил по имеющейся, различающихся мощностью терм-множеств нечетких переменных (НП) и универсумов. Актуальность проблемы для синтеза адаптивного нечеткого регулятора (АНР) обусловлена тем, что первоначальное расположение функций принадлежности (ФП) термов НП “управляющее воздействие” на универсальном множестве может быть произвольным [2]. Связь входных и выходных сигналов регулятора основного контура в базе правил осуществляется путем определения соответствий посылок заключениям, определенными терм множествами НП “управляющее воздействие”. Такая база правил используется в самом начале процесса адаптации перед ее изменением в процессе управления.
Первоначальное положение ФП термов выходной переменной существенно влияет на длительность процесса адаптации. В случае расположения термов в начале координат универсума возможна потеря устойчивости замкнутой системы в начале процесса управления, связанная с медленным заполнением базы правил НР [3].
Устранить указанный недостаток можно с помощью априорного заполнения базы правил адаптивного НР с использованием правил неадаптивного НР или правил предложенных экспертами. Этот же механизм целесообразно использовать в случае замены неадаптивного регулятора адаптивным НР, при неудовлетворительном функционировании ОУ в результате “старения” элементов системы, дрейфа рабочих характеристик, изменения диапазонов сигналов и прочее. Основной задачей здесь является определение соответствия правил адаптивного НР, правилам неадаптивного НР или правилам предложенным экспертами из-за различий в мощности терм-множеств и области определения входных и выходных сигналов регуляторов.
Для решения задачи заполнения базы правил необходимо
- найти оператор растяжения (сжатия) универсальных множеств неадаптивного НР, для соответствия областей определения НП регуляторов;
- установить соответствия термов T и T’ НП регуляторов с некоторым пороговым значением α, путем расчета таблиц степеней соответствий, для последующего формирования посылок и заключений правил;
- модифицировать таблицы степеней соответствий так, чтобы каждый элемент T’
При разработке алгоритма априорного заполнения базы правил в качестве исходных данных, примем абстрактную базу правил заданную экспертами, представленную в табл. 1.
Таблица 1. Заданная база правил неадаптивного НР
| Nu | Ns | |||||
| Ts(1) | Ts(2) | ××× | Ts(ks-1) | Ts(ks) | ||
| Ne | Te(1) | Tu(1) | Tu(1) | ××× | Tu(ku-4) | Tu(ku-3) |
| Te(2) | Tu(2) | Tu(2) | ××× | Tu(ku-3) | Tu(ku-2) | |
| ××× | ××× | ××× | ××× | ××× | ××× | |
| Te(ke-1) | Tu(ku-6) | Tu(ku-5) | ××× | Tu(ku-1) | Tu(ku-1) | |
| Te(ke) | Tu(ku-5) | Tu(ku-4) | ××× | Tu(ku-1) | Tu(ku) | |
Пусть в исходной базе правил определены терм-множества Ti переменных Ni на универсумах Li и заданы их ФП. Необходимо реализовать априорное заполнение базы правил АНР с переменными N’i с терм множествами T’i на универсумах L’i (i=1, 2, 3). Для этой цели необходимо выполнить последовательность шагов.
Шаг 1. Применить оператор растяжения (сжатия) K: Li®Li*, Li*ÎLi‘, “Ni, i=1,2,3. Для растяжения (сжатия) областей определения L в L* можно использовать аффинное преобразование координат, которое имеет вид
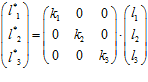 , (1)
, (1)
где 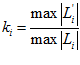 – коэффициент преобразования.
– коэффициент преобразования.
Шаг 2. Установить соответствия между T и T’. Вычислить степени соответствия для всех T и T’ каждой из трех НП
mk(l’)=max{min{mi(l’), mj(l*)}}³α, “i, j. (2)
где α – пороговое значение (0
£
α
£ 1), i – номер терма переменной неадаптивного НР, j – номер терма переменной АНР.
Результаты занести в таблицы соответствий S1, S2 и S3.
Шаг 3. Модифицировать степени соответствия термов входных НП путем присвоения
S1(i1, j1)=0, S1(:, j1)<max(S1(:, j1)), (3)
S2(i2, j2)=0, S2(:, j2)<max(S2(:, j2)), (4)
где i1, i2 – номера термов входных переменных неадаптивного НР, j1, j2 – номера термов выходных переменных АНР, “:” – все элементы столбца.
Шаг 4. Выбрать правила в базе правил (B1) неадаптивного НР с заключениями соответствующими терму с k-м номером для выходной переменной.
Шаг 5. Определить номера соответствующих термов (v, z) входных переменных в посылках найденных правил.
Шаг 6. Определить множество номеров термов (L, P) входных переменных АНР соответствующих найденным v, z в таблицах соответствий S1, S2.
Шаг 7. Определить в таблице соответствия S3 номера термов (n) выходной переменной в строке k по формуле
max(min(L, P))®max(S3(k, :))®n,
где “:” – все элементы строки.
Шаг 8. Внести в таблицу правил АНР
B2(l, p)=n.
Выполнить этапы 7, 8 для всех элементов из L, P.
Шаг 9. Нарастить k=k+1 и перейти к шагу 4.
Шаг 10. Конец.
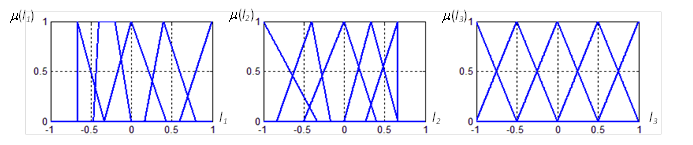
Пример. Пусть заданы НП N1, N2 и N3. Функции принадлежности терм-множеств НП (T={ОБ – отрицательно большое, ОС – отрицательно среднее, Н – нулевое, ПС – положительно среднее, ПБ – положительно большое}) показаны на рис. 1.
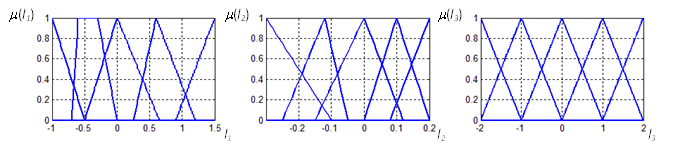
а б в
Рисунок 1. Функции принадлежности НП N1, N2 и N3 НР
Задана база правил неадаптивного НР в виде табл. 2.
Таблица 2. База правил неадаптивного НР
| N3 | N2 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| N1 | 1 | 5 | 5 | 5 | 4 | 3 |
| 2 | 5 | 5 | 4 | 3 | 2 | |
| 3 | 5 | 4 | 3 | 2 | 1 | |
| 4 | 4 | 3 | 2 | 1 | 1 | |
| 5 | 3 | 2 | 1 | 1 | 1 | |
Для компактности записи лингвистическим названиям термов присвоены численные наименования: ОБ – 1, ОС – 2, Н – 3, ПС – 4, ПБ – 5.
Необходимо заполнить базу правил АНР со следующими НП и их параметрами
N’1, T’1={-1, -0,8, …, 0, …, 0,8, 1}, L’1=[-1, 1],
N’2, T’2={-1, -0,8, …, 0, …, 0,8, 1}, L’2=[-1, 1],
N’3, T’3={сi}, L’3=[-1, 1],
где 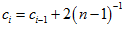 в соответствии с формулой (**88), n=11´11=121.
в соответствии с формулой (**88), n=11´11=121.
На рис. 2 показаны ФП термов переменных АНР.
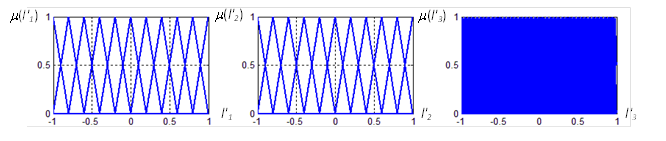
а б в
Рисунок 2. Функции принадлежности термов НП N’1, N’2 и N’3 АНР
Функции принадлежности термов переменных N’1 и N’2 треугольные, симметричные, равномерно распределенные на универсальных множествах L’1 и L’2
с пересечением на уровне 0,5. Функции принадлежности термов переменной N’3 треугольные, симметричные, равномерно распределенные на универсальном множестве L’3. Находим коэффициенты преобразования k1=1/1,5=0,75, k2=1/0,3=10/3, k3=0,5. Вид ФП неадаптивного НР после преобразования показан на рис. 3.
а б в
Рисунок 3. Функции принадлежности термов НП N1, N2 и N3 НР после масштабирования
В табл. 3 показан пример вычисления степеней соответствия термов НП N1 и N’1 по формуле (2) и модификации по формулам (3), (4).
Таблица 3. Степени соответствия термов НП N1 и N’1
| N’1 | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| N1 | 1 | 0 | 0,33 | 0,875 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0,684 | 0 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,665 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,665 | 1 | |
Видно, что степени соответствия терму 1 НП N’1 равны нулю. Это связано с отсутствием термов у НП N1 (см. рис. 3, а) для l1<0,7.
Результаты выполнения шагов 4-10 приведены в табл. 4.
Таблица 4. Таблица правил АНР
| N’3 | N’2 | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| N’1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 119 | 119 | 110 | 110 | 104 | 104 | 85 | 85 | 67 | 67 | 0 | |
| 3 | 121 | 120 | 111 | 112 | 105 | 106 | 96 | 86 | 67 | 67 | 0 | |
| 4 | 117 | 116 | 107 | 108 | 95 | 87 | 66 | 56 | 26 | 36 | 0 | |
| 5 | 118 | 116 | 107 | 109 | 95 | 94 | 66 | 56 | 26 | 36 | 0 | |
| 6 | 115 | 114 | 93 | 89 | 57 | 64 | 27 | 34 | 10 | 12 | 0 | |
| 7 | 113 | 113 | 88 | 88 | 65 | 65 | 35 | 35 | 11 | 12 | 0 | |
| 8 | 91 | 90 | 63 | 59 | 33 | 29 | 5 | 4 | 13 | 15 | 0 | |
| 9 | 92 | 92 | 58 | 58 | 28 | 28 | 6 | 6 | 14 | 15 | 0 | |
| 10 | 62 | 62 | 32 | 32 | 3 | 3 | 9 | 9 | 17 | 18 | 0 | |
| 11 | 61 | 60 | 30 | 31 | 2 | 1 | 8 | 7 | 16 | 18 | 0 | |
Полученная база правил содержит исходные данные АНР, пригодные для дальнейшей модификации адаптивным алгоритмом.
Библиографический список
- Kok Wai Wong, Domonkos Tikk, Tamas D. Gedeon, Laszalo T. Koczy. Fuzzy rule interpolation for multidimensional input spaces with applications: a case study // IEEE Transactions on fuzzy systems, vol. 13, NO. 6, December 2005. pp. 809-819.
- Соловьев В.В., Финаев В.И. Методика синтеза адаптивного нечеткого регулятора для объекта с неопределенной моделью // Известия ЮФУ. Технические науки. Тематический выпуск. – Таганрог: Изд-во ТТИ ЮФУ, № 1 (126), 2012. – С. 78-83.
- Соловьев В.В. Оценка устойчивости в системах с адаптивным нечетким регулятором // Материалы всероссийской научной конференции “Актуальные проблемы современности: человек, общество, техника” – часть 3 – Таганрог: Изд-во ТТИ ЮФУ, 2012 – 54 с.
Количество просмотров публикации: Please wait


