Часто необходимо проверить схожесть алгоритма двух технологических программных цепочек состоящих из многочисленных типовых программ(длинные цепочки).[1] Например: сортировка, слияние, форматирование для печати, промежуточная и итоговая печать, сравнение с различными справочниками и т.д. Присваивая каждой программе свой порядковый номер, можно легко определить степень последовательной схожести или расхождения двух программ с помощью рангово -бисериального коэффициента Гласса. Если коэффициент больше или равен 0,5,можно говорить о схожести программного алгоритма, если менее 0,5 то алгоритмы самостоятельны и имеют слабо коррелирующие между собой структуры .
Рангово – бисериальный коэффициент основан на сравнении линейной последовательности, элиминируя влияние дисперсии и среднеквадратических отклонений и пр.С помощью рангово – бисериального коэффициента, можно осуществить сортировку и группировку информационных данных по позициям схожести алгоритма обработки данных. [1]
Каждой программе можно присвоить определенный код или номер.(например:1,2,3,4.5).Запуская параллельно сразу 5 программ, можно снимать результаты в четырех мгновениях времени. Коэффициент конкордации покажет согласованность работы программ или наоборот хаотичность работы при обработки пяти программ.
Коэффициент конкордации[2 ]:
W=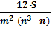 , где S разность между суммы квадратов сумм по строкам и средним квадратом суммы строк.
, где S разность между суммы квадратов сумм по строкам и средним квадратом суммы строк.
S=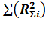 –
– 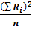 ,то есть структурная степенная функция минус средняя агрегатная форма функции, то есть S структурная разница.(R может обозначаться как Х).
,то есть структурная степенная функция минус средняя агрегатная форма функции, то есть S структурная разница.(R может обозначаться как Х).
Другими словами коэффициент конкордации это структурная степенная разница приходящаяся на единицу площади матрицы(таблицы).
Если рассматриваем только два признака Х и У, рассчитывают коэффициент парной регрессии, который имеет ту же основу, что и коэффициент конкордации[2]:
АR =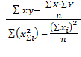 Эта формула выведена из системы линейных уравнений:
Эта формула выведена из системы линейных уравнений:
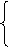 а0n + a1Sx = Sy
а0n + a1Sx = Sy
а0Sx + a1Sx2 = Sxy
Эти системы линейных уравнений являются модификациями линейной функции: Y=a0+
a1x
По сути коэффициент парной регрессии это параметр а0 , выведенный по системе линейных уравнений 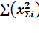 и
и 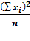
Сумма Xij возведенная в квадратную степень, называемая агрегатной суммой, разделенная на количество исследуемых объектов, покажет значение неструктурного, агрегатного среднего элемента.
Сумма элементов сумм по строке возведенных в квадрат учитывает разбиение общего массива на кластеры и называется структурной суммой.
Разность вышеуказанных значений покажет степень разбиения массива на кластеры.
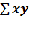 сумма произведения двух признаков по каждой строке,
сумма произведения двух признаков по каждой строке,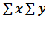 - произведение суммы признака Х и суммы признака У, так же будут обозначать агрегатную и структурную сущность суммового показателя.
- произведение суммы признака Х и суммы признака У, так же будут обозначать агрегатную и структурную сущность суммового показателя.
Разность между этими значениями так же будет отражать степень разбиения признаков на структурные ступени .
Что бы установить степень схожести (сопряженности) двух альтернативных признаков (дихотомию) явления, вычисляют рангово –бисериальный коэффициент Гласса. Он устанавливает степень зависимости таких признаков, на уровне параллельных плоскостей.
Распространено применение коэффициента парной регрессии и конкордации при определении уровня согласованности очередности запуска программ.
Чем больше значения коэффициента, тем сильнее синхронность работы программ. Например, рассмотрим пример синхронизации работы системы по обработки конкретной информации.
| Уровни времени работы рабочего задания | Обращение к программам раб.задания |
||||||||
Выстроенные цепи последовательности
RSi
RSi2
ABCDEFG1
3153112
16
256
2
1232226
18
324
3
2516431
22
484
4
6664365
36
1296
5
4441544
26
676
6
5325653
29
841
Итого: S(RSi)=147S(RSi2)=3877
Работают всего 6 рабочих заданий. Они обрабатывают один и тот же алгоритм программ. В шесть моментов времени снимаются данные по работающим программам(их так же 6).
A,B,C,D,E,F -рабочие задания по обработке данных
Исходные данные таблицы – это программы, которые должны отработать на определенном уровне.
Формула коэффициента конкордации [2]:
W=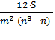 =
=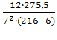 =
=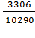 = 0,321
= 0,321
S=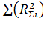 –
– 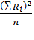 = 3877-
= 3877- 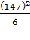 =3877 -
=3877 -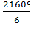 =3877-3601,5 = 275,5 Значение коэффициента конкордации равное 0,321 означает среднестатистическую согласованность, то есть синхронность работы исходного множества элементов.
=3877-3601,5 = 275,5 Значение коэффициента конкордации равное 0,321 означает среднестатистическую согласованность, то есть синхронность работы исходного множества элементов.
Если необходимо определить парную зависимость двух информативных признаков, рассчитывают коэффициент парной регрессии.
Коэффициент парной регрессии покажет линейное совпадение тенденции двух признаков.[2]
Например даны показатели времени работы рабочих заданий и количество программных блоков, составляющих алгоритм задания.
| Моменты наблюдения. Постоянный отрезок времени -через шаг h. |
Скорость работы программы в задании Операций в секунду X |
Количество отработанных блоков данных Y |
X2 |
XY |
| 1 |
6,0 |
2 |
36,00 |
12,0 |
| 2 |
6,1 |
3 |
37,21 |
18,3 |
| 3 |
6,8 |
6 |
46,24 |
40,8 |
| 4 |
7,2 |
4 |
51,84 |
28,8 |
| 5 |
7,4 |
2 |
54,76 |
14,8 |
| 6 |
7,9 |
3 |
62,41 |
23,7 |
| 7 |
8,2 |
4 |
67,24 |
32,8 |
S |
SX=49,6 | SY=24 | SX2=355,7 | SXY =171,2 |
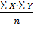 =
= 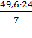 = 170,1;
= 170,1;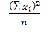 =
=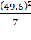 = 351,4 ;
= 351,4 ;
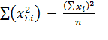 355,7-351,4= 4,3
355,7-351,4= 4,3
АR =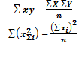 =
=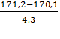 =0,26
=0,26
Такое значение коэффициента парной регрессии означает среднестатистическую согласованную линейность двух признаков X и Y,то есть их неярко выраженную синхронную зависимость, так как чем больше значение коэффициента конкордации, тем больше регрессия (не связь) между линейными тенденциями признаков.
Вывод- имеется не очень сильная линейная зависимость между работой программ- скоростью операций в секунду и количеством обработанных блоков данных.
 Если имеется две линии развития явления, или две серии зависимостей можно применить рангово – бисериальный коэффициент Гласса. Результаты расчетов этого коэффициента помогут исследовать связь анализируемых признаков.
Если имеется две линии развития явления, или две серии зависимостей можно применить рангово – бисериальный коэффициент Гласса. Результаты расчетов этого коэффициента помогут исследовать связь анализируемых признаков.
Например, проверяем уровень работы техники двух известных фирм. Для этого со стартового момента времени на заданных моделях техники необходимо обработать определенную информацию одно и то же задание для всех. Затем в контрольный момент времени был измерен процент выполненного задания. Нам необходимо определить имеется ли связь лучшей работы по выполнению задания и фирмой технических средств.
Коэффициент Гласса[2]:
| № Тех.средств |
% выполн.задания | Rmax по строке |
X Принадлежность фирме значений Rmax |
Y Ранжированный ряд Rmax |
|
| Фирма 1 | Фирма2 | ||||
| 1 |
18,33 |
18,46 |
18,46 |
2 |
5 |
| 2 |
13,33 |
19,41 |
19,41 |
2 |
4 |
| 3 |
18,33 |
32,82 |
32,82 |
2 |
1 |
| 4 |
8,33 |
9,74 |
9,74 |
2 |
9 |
| 5 |
6,68 |
6,67 |
6,68 |
1 |
10 |
| 6 |
20,00 |
30,77 |
30,77 |
2 |
2 |
| 7 |
16,07 |
23,59 |
23,59 |
2 |
3 |
| 8 |
16,67 |
11,28 |
16,67 |
1 |
7 |
| 9 |
18,33 |
8,72 |
18,33 |
1 |
6 |
| 10 |
1,67 |
1,03 |
1,67 |
1 |
11 |
| 11 |
15,00 |
7,18 |
15,00 |
1 |
8 |
В итоге получаем следующие сводные данные по двум фирмам:
|
X ФИРМЫ |
Y ранги |
|
X1 |
10+7+6+11+8 |
|
X2 |
5+4+1+9+2+3 |
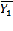 =
= 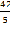 =8,4
=8,4
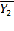 =
= 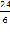 =4,0
=4,0
R=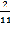 ×
× 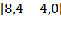 =0,8
=0,8
Означает сильную связь между скоростью обработки информации и фирмой к которой относятся технические средства на которых производится работа с данными.
При обучении информатикой, корреляция математически-статистических методов и информатики позволяет дать ученикам больше информации и знаний ,научить логически мыслить и применять на практике математический опыт работы с данными.
Библиографический список
-
Справочник по информатике; М:,Энциклопедия,2010
-
Математические и статистические методы в информатике: Краткий справочник для специалистов; М:,Энциклопедия,2007
