Научный руководитель: Вильданов Алмаз Нафкатович
к.ф.-м.н., Уфимский университет науки и технологий, Нефтекамский филиал
Цель проекта
Разработать и верифицировать модель генерации и проверки электронной подписи по алгоритму RSA с использованием математического ПО Maple для обеспечения целостности и аутентичности цифровых данных.
Задачи проекта
1. Реализовать функции конвертации текста в числовой формат (`str_to_num_eng`) и обратно (`num_to_str_eng`) на основе кодов ASCII.
2. Сгенерировать ключевую пару RSA: секретный и открытый.
3. Создать электронную подпись для сообщения “VAN”.
4. Проверить подлинность подписи с помощью открытого ключа.
5. Проанализировать работу криптографических функций Maple.
Шифрование RSA (Rivest-Shamir-Adleman) — это широко используемая криптосистема с открытым ключом, основанная на сложности разложения больших чисел на множители. «Большие числа», используемые в современных системах RSA, обычно имеют длину более 300 знаков после запятой или 1024 бит, и их чрезвычайно трудно разложить на множители с помощью алгоритмов и вычислительной мощности, доступных в настоящее время. Такие системы избавляют от необходимости в общем ключе. Обмен информацией инициируется держателем приватного ключа. Любая сторона, желающая отправить сообщение, может зашифровать отправляемое сообщение с помощью открытого ключа. Только держатель закрытого ключа может расшифровать зашифрованный текст; Сложность разложения на множители таких больших чисел делает практически невозможным для перехватывающих сторон расшифровку сообщения.
Реализация функций преобразования текста
Для работы алгоритма RSA разработаны функции:
- «str_to_num_eng(s)» – конвертирует строку в число путём преобразования каждого символа в двузначный код ASCII (смещённый на 64):

Пример:
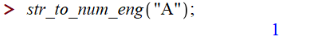
(т.к. Ord(“A”)=65 → 65-64=01).
- «num_to_str_eng(n)» – выполняет обратное преобразование:

Пример:

Генерация ключей RSA
1. Выбор простых чисел:
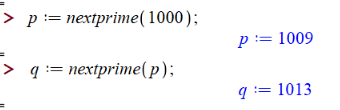
2. Расчёт модуля и функции Эйлера:
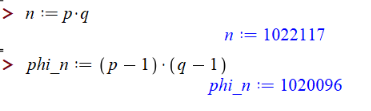
3. Выбор открытой экспоненты `e` (взаимно простое с `phi`):

1 означает, что условие выполнено.
4. Расчёт секретной экспоненты `d` через расширенный алгоритм Евклида:
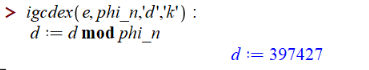
Создание и проверка подписи для сообщения “VAN”
1. Преобразование текста в число:
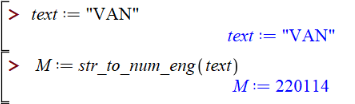
2. Генерация подписи:
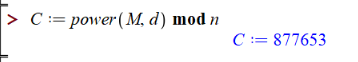
3. Верификация подписью:

Вывод
Моделирование в Maple подтвердило работоспособность алгоритма RSA для создания и проверки ЭЦП. Ключевые особенности:
- функции «str_to_num_eng»/ «num_to_str_eng» обеспечивают корректное преобразование текста;
- генерация ключей с использованием «nextprime», «igcdex» гарантирует криптостойкость;
- применение теоремы Эйлера (M^ed ≡ M mod n) обеспечивает верификацию подписи.
Электронные подписи на основе RSA широко используются в ЭДО, цифровых сертификатах (TLS), блокчейне и защищённых коммуникациях.
Библиографический список
- RSA Encryption / [Электронный ресурс] // Maplesoft : [сайт]. — URL: https://www.maplesoft.com/support/help/maple/view.aspx?path=MathApps/RSAEncryption (дата обращения: 03.06.2025).
- RSA Encryption / [Электронный ресурс] // MathWorld : [сайт]. — URL: https://mathworld.wolfram.com/RSAEncryption.html (дата обращения: 03.06.2025).
- Федеральный закон “Об электронной подписи” № 63-ФЗ. — http://www.consultant.ru (дата обращения: 03.06.2025).
- Национальный стандарт РФ ГОСТ Р 34.10-2012 “Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи” (утв. приказом Федерального агентства по техническому регулированию и метрологии от 7 августа 2012 г. N 215-ст).
