Актуальность разработки (цель исследования) обоснована тем, что в настоящий момент в связи с экономической политикой Российской Федерации по импортозамещению любой производящийся программно-аппаратный продукт в нашей стране может иметь какие-либо скрытые дефекты. Необходимо разработать комплекс критериев и метрик оценивания надёжности какого-либо программного продукта.
В связи с этим попробуем выполнить эту задачу на примере игрушки «Тетрис».
Основной функционал:
Случайные фигурки тетрамино падают сверху в прямоугольный стакан шириной 10 и высотой 20 клеток. В полёте игрок может поворачивать фигурку на 90° и двигать её по горизонтали. Также можно «сбрасывать» фигурку, то есть ускорять её падение, когда уже решено, куда фигурка должна упасть. Фигурка летит до тех пор, пока не наткнётся на другую фигурку либо на дно стакана. Если при этом заполнился горизонтальный ряд из 10 клеток, он пропадает и всё, что выше него, опускается на одну клетку. Дополнительно показывается фигурка, которая будет следовать после текущей — это подсказка, которая позволяет игроку планировать действия. Темп игры постепенно ускоряется. Игра заканчивается, когда новая фигурка не может поместиться в стакан. Игрок получает очки за каждый заполненный ряд, поэтому его задача — заполнять ряды, не заполняя сам стакан (по вертикали) как можно дольше, чтобы таким образом получить как можно больше очков.
Цель: развивать сообразительность, память, воображение ребёнка, знакомить с цветом, формой, величиной, а также способствовать развитию речи, развивать мелкие мышцы рук.
Требования к оборудованию:
В качестве аппаратной среды используется ПК типа IBM PC.
Системные требования:
1. Компьютер Pentium 200 МГц
2. Оперативная память 32 RAM
3. Видеокарта 800х600
4. Операционная система Microsoft Windows 98/ME/2000/XP/Vista/7
5. Клавиатура
6. Мышь
7. Размеры свободного дискового пространства 200 кб
Теперь оценим надёжность данного программного продукта по четырём критериям:
Зрелость:
Метрика “Объем модуля”. Как правило, наиболее весомые модули имеют больший объем кода. Если обозначить: А — объем модуля (например, число строк кода); В — объем кода аналогичного по функциональности модуля, взятый из статистических данных организации разработчика программного средства, то числовую оценку метрики можно найти по формуле
X =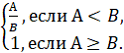
При этом справедливо 0<А; 0<X<=1.
В качестве модуля A возьмём весь код программы. Он содержит 10+68+4+119+12+128+18+11 = 370 строк кода из всех подмодулей.
В качестве модуля B возьмём весь код программы разработчика данного средства.
Он содержит 142 + 194 + 54 = 390 строк кода из всех подмодулей.
X = 370/1029 = 0,356.
Метрика “Время, затраченное на разработку модуля”. Как правило, на разработку наиболее весомого модуля затрачивается больше времени. Если обозначить: А — время, затраченное на разработку модуля; В — время, затраченное на разработку аналогичного по функциональности модуля, взятое из статистических данных организации-разработчика программного средства, то числовую оценку метрики можно найти по формуле
X =.gif)
При этом справедливо 0<А; 0<X<=1.
Пускай время будет исчисляться в часах. У одного разработчика на создание общего, функционально простого модуля ушло 32 часа. У команды из пяти человек на создание общего модуля с клиентским уклоном ушло 70 часов.
Получаем что Х = А/B = 0,457
Метрика “Потребляемые ресурсы модулем”. Как правило, более весомый модуль потребляет и больше ресурсов. Если обозначить: А — объем потребляемых ресурсов модулем (объем оперативной памяти и т.п.); В — общий объем потребляемых программным средством ресурсов, то числовую оценку метрики можно найти по формуле X=A/B. При этом справедливо: 0<А < B; 0< X <1.
В качестве потребляемых ресурсов взята используемая оперативная память, а программным средством является студия разработки модуля InteliJ IDEA Community Edition.
Под модулем подразумевается наше ПО. Оно потребляет 0,036 Мб оперативной памяти компьютера.
Для нормальной работы InteliJ IDEA требуется 1200 Mб оперативной памяти.
Х = A/B = 0,036/1200 = 0,00003
Способность к восстановлению:
Метрика “Зависимость модулей”. Как правило, в программном средстве модули связаны в древовидную структуру, где неправильная работа одного модуля приводит к неправильной работе других модулей. Если обозначить: А — количество модулей, зависящих от данного модуля; В — общее количество всех модулей, то числовую оценку метрики можно найти по формуле X=A/B. При этом справедливо 0<=А < B; 0< X <1.
Пускай под модулями будем подразумевать классы (структуры) программы. Всего классов у программы восемь. Все они связаны между собой. Поэтому X=A/B = 1 / 8 = 0,125
Метрика “Частота использования модуля”. Вероятность появления ошибки возрастает с ростом количества вызовов модуля, поэтому часто вызываемые модули более весомы, нежели модули, вызываемые реже.
Если обозначить: А — количество вызовов модуля; В — общее количество всех вызовов модулей, то числовую оценку метрики можно найти по формуле X=A/B. При этом справедливо 1<=А < B; 1/B< X <1.
Пускай под вызовами моделей будем иметь ввиду событие нажатия кнопки интерфейса программы либо нажатие клавиши на клавиатуре.
Используя клавиши со стрелками влево, вправо и вверх мы заставляем падающую сверху фигуру менять своё местоположение в пространстве. Задействовано 3 модуля т.е. А=3. Четвёртым не всегда задействованным модулем будет являться клавиша со стрелкой вниз. Она отвечает за скорость падения фигуры.
Итак, X=A/B = 3 / 4= 0,75
Метрика “Время работы модуля”. Как правило, чем большее время находится модуль в работе, тем он более весом. Если обозначить: А — время работы модуля; В — общее время выполнения всей задачи, то числовую оценку метрики можно найти по формуле X=A/B. При этом справедливо 0<А<B; 0<X<1
Стандартное время выполнения модуля А – 90 секунд.
Время выполнения всей задачи – 120 секунд.
X =А/В=90/120 =0,75.
Соответствие стандартам:
Метрика “Команда разработки модуля”. Как правило, в разработке наиболее весомых модулей принимает участие большее количество разработчиков. Если обозначить: А — количество разработчиков, принимающих участие в разработке модуля; В — количество разработчиков, принимавших участие в создании аналогичного по функциональности модуля, взятое из статистических данных организации-разработчика программного средства, то числовую оценку метрики можно найти по формуле
X =.gif)
При этом справедливо 0<А; 0<X<=1.
Под модулем A будем считать кол-во разработчиков данного программного продукта. Участие принимал один разработчик.
В — количество разработчиков, принимавших участие в создании аналогичного по функциональности модуля.
Предположим, это будут: Аналитик – человек отвечающий за анализ ТЗ и сбор информации, человек отвечающий за создание переменных и логику программы, человек отвечающий за интерфейс программы, человек отвечающий за компоновку всех подмодулей и работоспособность программы в целом, тестировщик. Всего пять человек.
X =1/5 = 0,2.
Метрика “Квалификация команды разработчиков”. Как правило, в разработке наиболее весомых модулей принимают участие более квалифицированные разработчики. Если обозначить: А — уровень квалификации команды разработчиков, принимающих участие в разработке модуля (А — может быть определенно экспертным путем, 0<А<=1); В — уровень квалификации команды разработчиков, принимавших участие в создании аналогичного по функциональности модуля, взятый из статистических данных организации-разработчика программного средства, то числовую оценку метрики можно найти по формуле
X =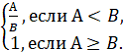
При этом справедливо 0<А<=1; 0<X<=1.
В разработке данного модуля принимал участие один человек. Его уровень – юниор – оценивается единицей. Команда разработчиков предприятия имеет уровень – опытный – оценивается числом 2.
X =A/B = 1 / 2= 0,5
Метрика “Документирование модуля”. Как правило, более весомые модули должны иметь больший объем документации. Если обозначить: А — суммарный объем документов, описывающих анализируемый модуль; В — суммарный объем документов аналогичного по функциональности модуля, взятый из статистических данных организации-разработчика программного средства, то числовую оценку метрики можно найти по формуле
X =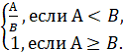
При этом справедливо 0<А;0<X<=1
Под документацией будем подразумевать всю информацию, касающуюся конкретно данного модуля.
Пусть А будет включать только список файлов, позволяющих использовать модуль на сторонних аппаратных средствах. Их будет 5.
B – будет включать тот же список необходимых документов. Но добавятся три новых: ТЗ, спецификации и доклад руководству.
X =A/B = 5/ 8= 0,625
Отказоустойчивость:
Метрика “Тестовые наборы модуля”. Как правило, более весомые модули имеют большее количество тестовых наборов данных. Если обозначить: А — количество тестовых наборов разрабатываемого модуля; В — количество тестовых наборов аналогичного по функциональности модуля, взятое из статистических данных организации-разработчика программного средства, то числовую оценку метрики можно найти по формуле
X =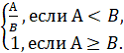
При этом справедливо 0<А;0<X<=1
Так как объём исходного модуля и модуля организации-разработчика почти различаются, функционал также будет различен и кол-во тестовых наборов будет не одним и тем же. Организация-разработчик создала более масштабную программу с клиентским уклоном.
А = 1
B = 2
Х = А/В = 0,5
Метрика “Время тестирования модуля”. Как правило, более весомые модули тестируются более продолжительное время. Если обозначить А — время тестирования разрабатываемого модуля; В — время тестирования аналогичного по функциональности модуля, взятое из статистических данных организации-разработчика программного средства, то числовую оценку метрики можно найти по формуле
X =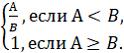
При этом справедливо 0<А; 0<X<=1.
Предположим, что разработчик исходной программы тестирует код белого ящика, а разработчик-тестировщик организации – код черного ящика.
Тогда параметр А будет равен 12 секундам.
Параметр В будет равен 600 секундам.
X = А/В = 0,02
Оценку надёжности программного средства будем проводить по формуле:
![]() =
=![]() ., где n – кол-во модулей в программном средстве
., где n – кол-во модулей в программном средстве
Si – вес i-го модуля
Pi – оценка надежности i-го модуля
![]() =
=.gif) ,
,![]() =1-
=1-![]()
Для оценки надёжности i-го модуля данную формулу использовать не будем, т.к пользователь никаких данных не вводит. Программа запускается при нажатии кнопки Run.
Программным продуктом является сама игра Тетрис, написанная на java. Её модулями являются классы. Их всего восемь. Пользователи игры доступа к модулям не имеют. Имеет доступ только сам разработчик и тестировщик. Поэтому будем рассматривать программный продукт с точки зрения тестировщика.
Пусть вероятность просмотра модулей равна соответственно 0,05;0,1;0,05;0,4;0,05;0,25;0,05;0,05.
Вероятность ошибки возможно в самых крупных по числу строк модулях. Это 4 и 6 модули. В четвёртом модуле произошла ошибка типа Medium, а в шестом – типа High.
Вес ошибок Priceless, High, Medium, Low, None, Detrimental соответственно равны 0,4; 0,25; 0,2; 0,1; 0,04; 0,01.
Тогда оценка надежности всех модулей будет равна:
P = 1 – (0 * 0,05+0*0,1+0*0,05+0,2*0,4+0*0,05;0,25*0,25;0*0,05;0*0,05)
P = 1 – 0,1425 = 0,8575
Чтобы рассчитать веса модулей, сначала найдём знаменатель. Он должен равняться 1:
.gif)
V1 = 0,356
V2 = 0,157
V3 = 0,00003
V4 = 0,025
V5 = 0,05
V6 = 0,15
V7 = 0,003
V8 = 0,1
V9 = 0,09
V10 = 0,05
V11 = 0,01897
Значения Xij возьмём из ранее найденных значений метрик:
X1 = 370/1029 = 0,356
Х2 = А/B = 0,457
Х3 = A/B = 0,036/1200 = 0,00003
X4=A/B = 1 / 8 = 0,125
X5=A/B = 3 / 4= 0,75
X6 =А/В=90/120 =0,75.
X7 =1/5 = 0,2
X8 =A/B = 1 / 2= 0,5
X9 =A/B = 5/ 8= 0,625
Х10 = А/В = 0,5
X11 = А/В = 0,02
Находим числитель по формуле
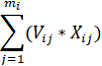
(0,356*0,356) +( 0,157*0,457) +( 0,00003*0,00003) +( 0,025*0,125) +
+(0,05*0,75) +(0,15*0,75) + (0,003*0,2) + (0,1*0,5) +(0,09+0,625) +
+ (0,05*0,5) +( 0,01897*0,02) = 0,1267+0,071+0,00000001+0,0031+
+0,0375+0,1125+0,0006+0,05+0,0562+0,025+0,0003 = 0,4829
Делим на единицу в знаменателе.
S = 0, 4829
Наконец находим оценку надёжности всего программного средства:
Pпс = P * S = 0,8575*0, 4829 = 0,414
Оценка надёжности программного средства показала, что данная программа является надёжной только на 40%.
В связи с этим рекомендуются следующие действия по увеличению надёжности ПП:
1. Проведение обширного тестирования (в особенности юнит-тесты, модульные тесты, интеграционные тесты, функциональные тесты);
2. Уменьшение числа классов (модулей программы) для лучшей производительности;
3. Постараться упростить функциональность (логику) программы, сделать код более гибким, не создавать лишнего.
4. Низкоуровневый подход к написанию кода (то есть создавать более простые структуры, методы поля, классы).
В любой технике, аппаратно-программном обеспечении, системе есть шанс возникновения отказа. Отказ — событие, заключающееся в нарушении работоспособного состояния объекта. В зависимости от целей исследования отказы подразделяют на: независимые и зависимые; внезапные и постепенные; параметрические и функциональные; конструкционные, производственные и эксплуатационные; перемежающие, сбои и т.д. Если пользователь (потребитель, покупатель, заказчик) хочет, чтобы его устройство прослужило ему как можно дольше, производитель обязан произвести оценку продукта по вышеуказанным критериям.
Библиографический список
- Дроботун, Е. Б. Надежность программного обеспечения. Виды и критичность ошибок [Электронный ресурс] / Е. Б. Дроботун. – 2009. – Режим доступа: http://www.ivtn.ru/2009/pdf/d09_04.pdf;
- Активная защита от отказов управляющих модульных вычислительных систем / И. Б. Шубинский [и др.]; под ред. И. Б. Шубинского. — СПб.: Наука, 1993;
- Безбогов, А. А.Безопасность операционных систем: учеб, пособие / А. А. Безбогов, А. В. Яковлев, Ю. Ф. Мартемьянов. — М: Машиностроение-!, 2007.
- Модели надежности программного обеспечения [Электронный ресурс]. – Режим доступа: http://works.doklad.ru/ view/rdN3bgvQO3s.html;
- Моисеев, М. Методы оценки надежности ПО [Электронный ресурс] / М. Моисеев. – Режим доступа: http://kspt.icc.spbstu.ru/media/files/2010/course/softwarequality/lec2.pdf
- Василенко, Н. В. Модели оценки надежности программного обеспечения [Текст] / Н. В. Василенко, В. А. Макаров // Вестник Новгородского государственного университета им. Ярослава Мудрого. – 2004. – № 28. – C. 126-132. – Режим доступа: http://cyberleninka.ru/article/n/modeli-otsenki-nadezhnosti-programmnogo-obespecheniya
- Тейер, Т. Надежность программного обеспечения. Анализ крупномасштабных разработок [Текст] / Т. Тейер, М. Липов, Э. Нельсон. – М.: Мир, 1981. – 323 с. – Режим доступа: http://www.twirpx.com/file/80443/
