Введение
В данной работе рассматриваются динамические объекты, математическими моделями которых являются сингулярно возмущенные системы (с малым параметром при части производных) с запаздыванием (по состоянию). Рассматривается задача оптимального управления по минимаксному критерию в постановке [1, 2] для сингулярно возмущенных систем с запаздыванием при неопределенных начальных условиях и интегральных квадратичных ограничениях на управляющие воздействия. Терминальный функционал качества зависит как от быстрых, так и от медленных переменных. В основе предлагаемого метода лежат идеи выделения асимптотики ансамбля траекторий сингулярно возмущенной системы, предложенные А.Г. Кремлевым в работе [3] но при отсутствии запаздывания и представления фундаментальной матрицы решений, разбитой на блоки в соответствии с размерностями быстрых и медленных переменных, в виде равномерно сходящейся последовательности [4]. Оптимальное решение аппроксимируется с любой заданной точностью (относительного малого параметра), при этом не требуется чрезмерных условий гладкости (дифференцируемость не выше первого порядка), ограничений на класс допустимых управлений.
1. Постановка задачи
Рассматривается управляемая сингулярно возмущенная система (с малым параметром ![]() при части производных) с постоянным запаздыванием
при части производных) с постоянным запаздыванием ![]() (по состоянию):
(по состоянию):
.gif) (1)
(1)где tT = [t0, t1]; xRn, yRm; uRr – управление. Начальное состояние системы (1) x(t) = (t), t0–h t t0, x(t0)=x0, y(t0)=y0 точно неизвестно и заданы лишь ограничения x0X0, y0Y0, X0, Y0 – выпуклые компакты в соответствующих пространствах, (t)(t), t0–h t t0 – заданное многозначное отображение со значениями в виде выпуклых компактов, непрерывное по t в метрике Хаусдорфа. Управление u(t), tT, – измеримые по Лебегу функции, удовлетворяющие условию
.gif) , =const > 0. (2)
, =const > 0. (2)Рассматривается минимаксная задача управления: среди управлений u()P найти u0 = u0(), доставляющее
где () заданная выпуклая функция (с конечными значениями); z=(x, y), z(t; u(), z0, ()), tT, – решение системы (1), исходящих из ![]() при некотором ()() и фиксированном u()P.
при некотором ()() и фиксированном u()P.
Выполнено условие экспоненциальной устойчивости для подсистемы быстрых переменных.
Запишем систему (1) в виде:
где матрицы A(t, ), G(t, ), B(t, ) имеют следующий блочный вид:
.gif)
.gif)
.gif)
Пусть Z[t,] – фундаментальная матрица решений системы (1) (при u 0), причем Z[,]=En+m, Z[t,]=0 при >t, E – единичная матрица. Матрицу Z[t,] представим в следующем блочном виде:
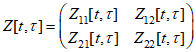
здесь Z11[t,], Z12[t,], Z21[t,], Z22[t,] – матрицы с размерами соответственно n![]() n, n
n, n![]() m, m
m, m![]() n, m
n, m![]() m.
m.
2. Аппроксимация решения задачи управления
Для реализации итерационной процедуры [5] построения оптимального решения задачи (3) важно правильно выбрать начальную асимптотику. Аппроксимация оптимального решения при ограничениях (2) существенно зависит [5] от вида разложения матрицы B2(t,) по параметру (0 0). Разрешимость исходной задачи управления, а также допустимость используемых аналитических конструкций определяется рядом требований [5]:
относительная управляемость вырожденной системы (система (1) при =0)dx/dt =A0(t)x(t)+G0(t)x(t–h)+B0(t)u
и подсистемы быстрых переменных dy/dt=A22(t1)y+B2(t1)u (стационарное условие управляемости), здесь
условия регулярности экстремальных элементов, обеспечивающие невырожденность условий оптимальности, в том числе в пограничном слое траекторий сингулярно возмущенной системы с запаздыванием.
Проведем исследование для случая, когда B1(t,)=B1(t), ![]() .
.
В [4] приведены рекуррентные формулы для вычисления блоков Zij[t,];(i,j = 1,2), определяющих асимптотику матрицы Z[t,] относительно малого параметра >0:
![]()
![]()
![]() k=0,1,2,…;
k=0,1,2,…;
причем ![]()
где ![]() фундаментальная матрица решений вырожденной системы, X[,]=En, X[t,]=0 при >t;
фундаментальная матрица решений вырожденной системы, X[,]=En, X[t,]=0 при >t; ![]() фундаментальная матрица решений системы
фундаментальная матрица решений системы
Справедлива следующая теорема [5].
Теорема 1. При 00, 0 достаточно мало справедливо
![]()
.gif)
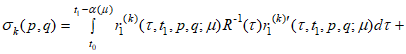
.gif)
где () 0, () = o(1), ()/ + при +0; функции ![]()
![]() определяются следующим образом:
определяются следующим образом:
![]()
.gif)
![]()
![]()
![]()
![]()
.gif)
где *(p, q) – сопряженная функция к (p, q); hk**(p,q)=![]() – замыкание выпуклой оболочки функции hk(p, q); (q | X) – опорная функция множества X на элементе q.
– замыкание выпуклой оболочки функции hk(p, q); (q | X) – опорная функция множества X на элементе q.
Рассмотрим управляющее воздействие ![]() :
:
.gif) (7)
(7)![]()
![]()
Теорема 2. [5] Пусть 0 0, 0 достаточно мало, ![]() доставляет оценку
доставляет оценку
3. Пример
Пусть исходная управляемая система (1) с запаздыванием описывается уравнениями:
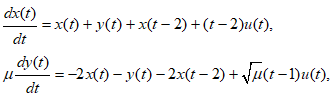 (8)
(8)где ![]()
![]()
![]() ;
; ![]()
![]() , малый параметр
, малый параметр ![]() .
.
Начальное состояние системы: при ![]()
![]() ,
,
при ![]()
![]()
![]() точно неизвестно и заданы лишь ограничения x0X0, y0Y0,: X0 – отрезок
точно неизвестно и заданы лишь ограничения x0X0, y0Y0,: X0 – отрезок ![]() Y0 – отрезок
Y0 – отрезок ![]() .
.
Управления u(t) удовлетворяют интегральному ограничению: ![]() , где
, где
.gif) .
.Обозначим z=(x, y), ![]() . Целевая функция
. Целевая функция ![]() .
.
Задача управления (3) состоит в том, что требуется в момент времени ![]() среди множества допустимых управлений найти такое оптимальное управление, чтобы перевести траекторию из множества Z0 в наименьшую окрестность точки 0.
среди множества допустимых управлений найти такое оптимальное управление, чтобы перевести траекторию из множества Z0 в наименьшую окрестность точки 0.
Наряду с исходной системой рассмотрим вырожденную систему (полученную из системы (8) при ![]() ):
):
На первом шаге итерации (при нулевом приближении) начнем с расчета фундаментальной матрицы вырожденной системы (9) ![]()
![]()
![]() при
при ![]() . Она находится методом последовательного интегрирования, по шагам относительно величины запаздывания [6]:
. Она находится методом последовательного интегрирования, по шагам относительно величины запаздывания [6]:
1) ![]() при
при ![]()
2) ![]() при
при ![]()
Таким образом, фундаментальная матрица ![]() вырожденной системы имеет вид: при
вырожденной системы имеет вид: при ![]()
где ![]() – функция Хэвисайда:
– функция Хэвисайда: ![]() .
.
Затем вычислим фундаментальную матрицу решений ![]() системы
системы
Далее на втором шаге итерации найдем блоки ![]()
![]() фундаментальной матрицы
фундаментальной матрицы ![]() исходной системы (8), причем
исходной системы (8), причем ![]()
![]() при
при ![]() .
. ![]() вычисляются по формулам (4). Интегралы представляются аналитическими, но громоздкими формулами, поэтому приведем их графики (Рисунок 1) в зависимости от разности времен
вычисляются по формулам (4). Интегралы представляются аналитическими, но громоздкими формулами, поэтому приведем их графики (Рисунок 1) в зависимости от разности времен ![]() .
.
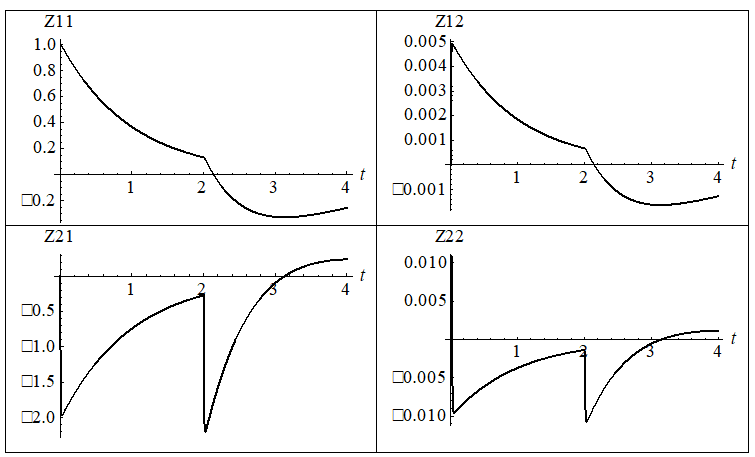 Рисунок 1. Элементы фундаментальной матрицы
Рисунок 1. Элементы фундаментальной матрицы ![]() на втором шаге итерации в зависимости от времени
на втором шаге итерации в зависимости от времени ![]()
Из соотношений (5) получим (при k=1)
То есть требуется найти максимум функции ![]() на окружности единичного радиуса
на окружности единичного радиуса ![]() , поэтому введем параметризацию p и q в виде:
, поэтому введем параметризацию p и q в виде:
В результате параметризации (9) получаем функцию ![]() (6), как функцию угла
(6), как функцию угла ![]() :
: ![]() . Вычисляем функцию
. Вычисляем функцию![]() по соотношениям (6), в формулах (6) в качестве
по соотношениям (6), в формулах (6) в качестве ![]() берем
берем ![]() , k=1.
, k=1.
Из структуры функции ![]() видно, что она является периодической с величиной периода
видно, что она является периодической с величиной периода ![]() . На Рисунке 2 показан график одного периода функции
. На Рисунке 2 показан график одного периода функции ![]() .
.

Максимальное значение функции ![]() : 0.219466 достигается при параметре
: 0.219466 достигается при параметре ![]() . Используя параметризацию p и q (9), находим, что максимальное значение функции
. Используя параметризацию p и q (9), находим, что максимальное значение функции ![]() достигается на единичном векторе
достигается на единичном векторе ![]() , где
, где
Оптимальное управление для задачи (3) ![]() определяется по формулам (7).
определяется по формулам (7).
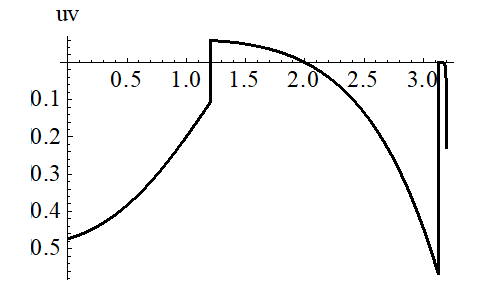
На Рисунке 3 приведена функция оптимального управления ![]() ,
, ![]() для задачи (3) в зависимости от текущего времени процесса
для задачи (3) в зависимости от текущего времени процесса ![]() . Оптимальное значение функционала качества для задачи (3)
. Оптимальное значение функционала качества для задачи (3)
Найдем законы движения фазовых переменных ![]() ,
, ![]() системы (8) в зависимости от времени
системы (8) в зависимости от времени ![]() при оптимальном управлении
при оптимальном управлении ![]() (7) и начальных состояниях: при
(7) и начальных состояниях: при ![]()
![]() , при
, при ![]()
![]()
![]() .
.
По формуле Коши [7] получаем: при ![]()
![]()
.gif)
.gif)
![]()
.gif)
.gif)
На Рисунке 4 представлен закон движения фазовых переменных ![]() ,
, ![]() при оптимальном управлении
при оптимальном управлении ![]() (7) и свободная эволюция начального состояния системы (8) при
(7) и свободная эволюция начального состояния системы (8) при ![]() .
.
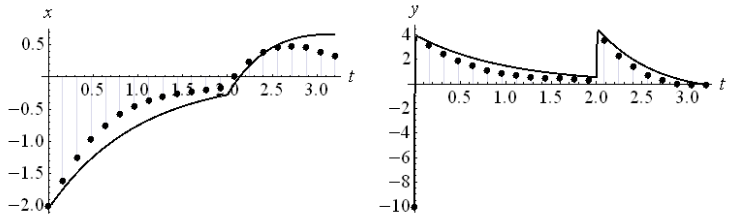 Рисунок 4. Зависимость координат x и y от времени t – точки. Свободная эволюция начального состояния (при u=0) – линия
Рисунок 4. Зависимость координат x и y от времени t – точки. Свободная эволюция начального состояния (при u=0) – линияВычислим значение функционала качества ![]() (3) переходных процессов
(3) переходных процессов ![]() системы (8) с вектором начальных состояний: при
системы (8) с вектором начальных состояний: при ![]()
![]() , при
, при ![]()
![]() , при оптимальном управлении
, при оптимальном управлении ![]() (7) и без управления (при
(7) и без управления (при ![]() ):
):
Заключение
Решена задача управления сингулярно возмущенной системой с запаздыванием при неопределенных начальных условиях и интегральных квадратичных ограничениях на ресурсы управления. Получены асимптотические представления (по малому параметру ) блоков фундаментальной матрицы уравнений управления, найдены рекуррентные формулы для вычисления блоков. Разработана итерационная процедура построения управляющего воздействия, аппроксимирующего оптимальное решение с заданной степенью точности относительно малого положительного параметра. Приведен модельный пример.
Библиографический список
- Красовский Н.Н. Теория управления движением. М., Наука, 1968.
- Куржанский А.Б. Управление и наблюдение в условиях. М., Наука, 1977.
- Кремлев А.Г. Асимптотические свойства ансамбля траекторий сингулярно возмущенной системы в задаче оптимального управления // Автоматика и телемеханика. 1993. № 9. С. 61-78.
- Гребенникова И.В. Об итерационном методе построения оптимального управления сингулярно возмущенными системами с запаздыванием // Известия Саратовского университета. Новая серия. Серия Математика. Механика. Информатика. 2009. Т. 9, вып. 3. С. 14-22.
- Гребенникова, И.В., Кремлев А.Г. Об итерационном методе построения оптимального управления сингулярно возмущенными системами с запаздыванием при квадратичных ограничениях // Известия Саратовского университета. Новая серия. Серия Математика. Механика. Информатика. 2011. Т. 11, вып. 3, ч. 1. С. 8-15.
- Мышкис А.Д. Линейные дифференциальные уравнения с запаздывающим аргументом. М., Наука, 1972.
- Беллман Р., Кук К. Дифференциально-разностные уравнения. М., Мир, 1967.
