КОМПЕНСАЦИЯ ОШИБОК ВОЗНИКАЮЩИХ ЗА СЧЕТ СЧИТЫВАНИЯ ИНФОРМАЦИИ С МАТРИЧНОГО ФОТОПРИЕМНИКА

В качестве датчиков изображений в наземных пассивных оптико-электронных системах специального назначения используются оптические телескопы с помещенными в их фокусе преобразователями “свет – сигнал”. [1]. Поскольку наиболее перспективными считаются в настоящее время матричные приборы с зарядовой связью (МПЗС) [2], разработку моделей обрабатываемых сигналов, снимаемых с оптических приемников, целесообразно провести применительно к указанному типу преобразователя “свет – сигнал”. Применение МПЗС вносит существенный вклад в качественные характеристики обнаружения и оценивания сигналов целей за счет изменения характеристик сигналов и шумов в процессе преобразования “свет – сигнал”.
В то же время МПЗС присущи физические явления, ограничивающие возможности качественного преобразования “свет – сигнал”. Некоторые из них приводят к потере электронов, составляющих фототок. Потеря электронов происходят как в процессе накопления заряда потенциальной ямы, так и при его транспортировке к выходу МПЗС [3, 4].
Оценим потери электронов, составляющих фототок, происходящие в процессе считывания изображения кадра. Будем считать, что МПЗС содержит  строк и  столбцов. Обозначим ,  вектор строку, элементами которой являются величины зарядов, возникающих в ячейках в результате накопления. В соответствии с рис. 1 параллельный аналоговый регистр осуществляет преобразование элементов вектора  при каждом сдвиге снимаемого изображения. Процедуру сдвига изображения кадра можно рассматривать как результат фильтрации каждой строки изображения в соответствующем фильтре. В результате выполнения указанной фильтрации вектор – строки , преобразуются в вектор – строки ,  по следующему правилу

           (1)

где  - соответствующие диагональные матрицы весовых коэффициентов фильтра  размера . Заметим, что матрицы весовых коэффициентов  могут быть представлены в виде соответствующих произведений матриц и имеют вид

           (2)

- диагональная матрица весовых коэффициентов фильтра размера  с элементами , равными коэффициентам передачи.

Систему уравнений (1) удобно записать с помощью матричного уравнения

           (3)

где , ,

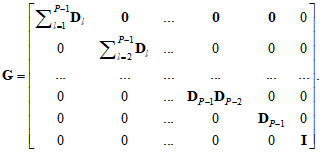
Последовательный сдвиг каждого из элементов изображения строки матрицы также может рассматриваться как результат обработки в фильтре размера , матрица весовых коэффициентов которого имеет вид

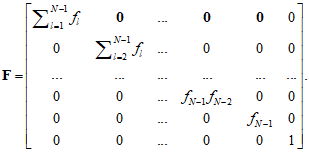
Это означает, что на выходе МПЗС получим вектор изображений в соответствии с выражением

           (4)

где

.

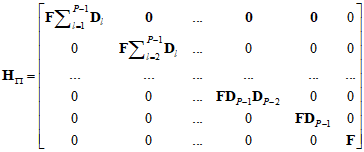Анализируя вид матрицы , приходим к выводу, что наибольшие искажения претерпевают изображения, которые находятся в верхнем левом углу изображения.
Поскольку коэффициенты фильтров  и ,  для всех МПЗС будут различными, их можно считать случайными величинами, а сами фильтры – фильтрами со случайными передаточными характеристиками. Для каждого конкретного МПЗС имеем неслучайную передаточную характеристику  фильтра. При этом можно утверждать, что  является невырожденной матрицей и имеет обратную, равную

.

Для того чтобы компенсировать ошибки, возникающие за счет считывания информации с МПЗС обратимся к формуле (4) и определению обратной матрицы . Умножение (4) слева на матрицу  позволяет разрешить его относительно исходного изображения

           (5)

Оценить  можно применяя в качестве исходного тест – изображение. Таким изображением может служить равномерная засветка, в соответствии с которой , где с – константа, зависящая от времени накопления. Тогда, считывая изображение, получим

           (6)

Умножая на  обе части (6), получим

           (7)

Заметим, что (7) можно разрешить, если ввести в рассмотрение псевдообратную матрицу к . Для получения однозначного решения необходимо, чтобы выполнялись следующие условия:

               (8)
           (9)
           (10)
           (11)

При соблюдении условий (8) – (11) матрица  будет псевдообратной матрицей Мура – Пенроуза для .
Псевдообратная матрица Мура – Пенроуза для  будет иметь вид . Докажем, что для матрицы  выполняется свойство (8):

а также свойство (9):

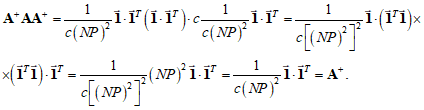
Выполнение свойств (10) и (11) очевидно.
Умножая на  справа обе части равенства (7), получим, что

           (12)

Таким образом, доказано, что, используя равномерную засветку, можно оценить для каждой конкретной МПЗС . Поскольку вычислить точно математическое ожидание по выборкам на конечном интервале наблюдения не представляется возможным, вместо истинного значения  будет получена ее оценка, которая в асимптотике сходится к истинному значению.

1. Верешкин А.Е. Телевизионная аппаратура оптико-электронного комплекса “Окно” // Вопросы радиоэлектроники. Сер. Техника телевидения. 2006. – Вып. 1. – С. 93 – 102.
2. Боксенберг А. Обзор основных тенденций в развитии приемников света // Оптические телескопы будущего. – М.: Мир, 1981. – С. 379 – 405.
3. Пресс Ф.П. Фоточувствительные приборы с зарядовой связью. – М.: Радио и связь, 1991. –264 с.
4. Лазовский Л. Приборы с зарядовой связью: прецизионный взгляд на мир. http:// http://www.autex.spb.ru/download/sensors/ccd.pdf.
5. И.В.Андрианов, Р.Г.Баранцев, Л.И.Маневич. Асимптотическая математика и синергетика: путь к целостной простоте. – М.: Едиториал УРСС, 2004. –  308 с.

Все статьи автора «Дашкин Эдуард Романович»