Задача обнаружения сигнала на фоне помех достаточно полно изучена для случая узкополосной радиолокации, когда принимается “прямой” сигнал
от цели на фоне пассивных помех, подчиняющихся гауссовскому закону распределения вероятностей [1,2]. При этом предполагается, что “прямой” отраженный сигнал может быть детерминированным, медленно или быстро флуктуирующим, сигналом от цели с доплеровским рассеянием.
В ряде других случаев плотность распределения вероятностей (ПРВ) амплитуд сигнала и помехи отлична от рэлеевской. Подобная ситуация возникает, когда отражения от подстилающей поверхности принимаются РЛС с высоким разрешением (длительность импульса составляет менее 0,5 мкс, угол места менее 5°). При этом у ПРВ амплитуд сигнала и помехи появляются так называемые “хвосты”. Механизм возникновения хвостов в настоящее время хорошо изучен и, как показали исследования [3,4], амплитуда может иметь распределение трех типов: логарифмически нормальное, Вейбулловское
и ![]() -распределение (Накагами). Фаза принимаемого сигнала является равномерно распределенной случайной величиной (СВ). Аналогичные результаты возникают при многолучевом распространении в связи [1].
-распределение (Накагами). Фаза принимаемого сигнала является равномерно распределенной случайной величиной (СВ). Аналогичные результаты возникают при многолучевом распространении в связи [1].
Цель работы состоит в том, чтобы сформулировать и решить задачу совместного обнаружения и оценивания прямого сигнала, принимаемого при наличии многолучевого распространения и помех в случаях, когда амплитуда имеет распределение одного из трех указанных выше типов.
принимаемого при наличии многолучевого распространения и помех
Задача совместного обнаружения и оценивания “прямого” сигнала на фоне помех, принимаемых при наличии многолучевого распространения, должна ставиться и решаться как задача проверки статистических гипотез ![]()
и ![]() . В соответствии с гипотезой
. В соответствии с гипотезой ![]() входной векторный СП
входной векторный СП ![]() содержит совокупность “прямого” сигнала
содержит совокупность “прямого” сигнала ![]() и
и ![]() компонент многолучевого сигнала
компонент многолучевого сигнала ![]() (
(![]() антиподов), принимаемых на фоне активных и пассивных помех. Вторая (альтернативная) гипотеза
антиподов), принимаемых на фоне активных и пассивных помех. Вторая (альтернативная) гипотеза ![]() состоит в том, что в принятой реализации
состоит в том, что в принятой реализации ![]() присутствуют все перечисленные выше компоненты кроме “прямого” сигнала. Математическая формулировка сказанного состоит в следующем:
присутствуют все перечисленные выше компоненты кроме “прямого” сигнала. Математическая формулировка сказанного состоит в следующем:
Формально для обнаружения “прямого” сигнала независимо от применяемого критерия качества необходимо сформировать отношение правдоподобия, его логарифм или достаточную статистику и сравнить одно из этих значений
с соответствующим порогом. Выбранный критерий качества определяет только величину порога. Вид обработки определяется из отношения правдоподобия, его логарифма или достаточной статистики. Учитывая сказанное, запишем выражение для функционала отношения правдоподобия при обнаружении “прямого” сигнала на фоне помех и многолучевого сигнала:
где ![]() и
и ![]() - функционалы плотности распределения вероятностей (ПРВ) векторного СП
- функционалы плотности распределения вероятностей (ПРВ) векторного СП ![]() при условии, что справедливы гипотезы
при условии, что справедливы гипотезы ![]() и
и ![]() .
.
Постановка задачи обнаружения в виде (1) весьма нереалистична поскольку “прямой” сигнал ![]() и совокупность мешающих многолучевых сигналов
и совокупность мешающих многолучевых сигналов ![]() , например для низколетящих целей, существовать отдельно друг от друга не могут. Поэтому (1) имеет смысл только в связи с другими задачами обнаружения. Чтобы убедиться в этом введем промежуточную гипотезу
, например для низколетящих целей, существовать отдельно друг от друга не могут. Поэтому (1) имеет смысл только в связи с другими задачами обнаружения. Чтобы убедиться в этом введем промежуточную гипотезу ![]() о том, что СП
о том, что СП ![]() содержит только компоненты помех и шумов, т.е.
содержит только компоненты помех и шумов, т.е. ![]() . Это позволяет записать (2) в виде [2]:
. Это позволяет записать (2) в виде [2]:
Входящее в (3) выражение ![]() - представляет собой функционал ПРВ векторного СП
- представляет собой функционал ПРВ векторного СП ![]() при условии, что справедлива гипотеза
при условии, что справедлива гипотеза ![]() .
.
Обращаясь к (3), замечаем, что первое частное представляет собой функционал отношения правдоподобия ![]() для проверки гипотез
для проверки гипотез ![]() и
и ![]() , а второе – является величиной, обратной функционалу отношения правдоподобия
, а второе – является величиной, обратной функционалу отношения правдоподобия ![]() для проверки гипотез
для проверки гипотез ![]() и
и ![]() . Учитывая сказанное, (3) запишем в виде:
. Учитывая сказанное, (3) запишем в виде:
Логарифм функционала отношения правдоподобия равен:
Соотношение (5) справедливо в случае, когда число лучей ![]() , а значит и антиподов априорно известно.
, а значит и антиподов априорно известно.
Задача обнаружения сигнала на фоне помех достаточно полно изучена для случая узкополосной связи и радиолокации, когда принимается “прямой” сигнал от цели на фоне пассивных помех, подчиняющихся гауссовскому закону распределения вероятностей [1,3,4]. При этом предполагается, что “прямой” сигнал может быть детерминированным или гауссовским, медленно или быстро флуктуирующим, сигналом от цели с доплеровским рассеянием.
Однако случай приема сигналов с амплитудой, отличной от рэлеевской, на фоне помех в условиях многолучевого распространения ни для одной из указанных выше задач не исследовался.
С математической точки зрения причина этого явления заключается в отсутствии аналитических выражений для ПРВ случайного процесса (СПр) с дискретным временем (или функционала ПРВ в случае непрерывного времени).
Поэтому решение указанной задачи потребовало разработки аналитических выражений для многомерных ПРВ СПр сигнала с амплитудой, распределенной по логарифмически нормальному, Вейбулловскому и ![]() (Накагами) законам распределения вероятностей. Фаза принимаемого сигнала является равномерно распределенной случайной величиной (СВ). Такие ПРВ названы модифицированными ПРВ (МПРВ) [5].
(Накагами) законам распределения вероятностей. Фаза принимаемого сигнала является равномерно распределенной случайной величиной (СВ). Такие ПРВ названы модифицированными ПРВ (МПРВ) [5].
Особенностью таких ПРВ является то, что они по своей сути, являются неустойчивыми распределениями относительно операции суммирования. Это означает, что вид ПРВ зависит от числа слагаемых в сумме и изменяется с добавлением каждого нового слагаемого. Неустойчивость таких ПРВ оказывает влияние на вид ПРВ суммы выборок сигнала с амплитудой, распределенной по логарифмически нормальному, Вейбулловскому, и ![]() (Накагами) законам распределения вероятностей. Фаза принимаемого сигнала является равномерно распределенной случайной величиной (СВ), и белого гауссовского шума.
(Накагами) законам распределения вероятностей. Фаза принимаемого сигнала является равномерно распределенной случайной величиной (СВ), и белого гауссовского шума.
Свертка двух ПРВ, подчиняющихся МПРВ Вейбулла и гауссовской ПРВ, соответствующая сумме двух СВ Вейбулла и гауссовской, определяется выражением:
.gif) (6)
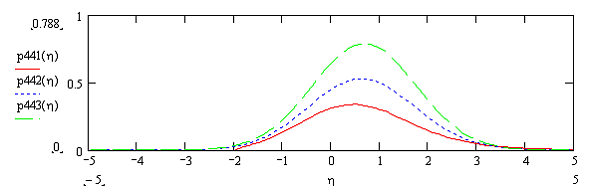
(6)Результаты расчетов по формуле (6) помещены в виде графиков на рисунке 1 для трех различных значений параметров ПРВ Вейбулла: ![]()
![]() ;
; ![]()
![]() ;
;![]()
![]() ;
; ![]() .
.![]() и
и ![]() - параметры распределения.
- параметры распределения.
Как следует из рисунка 1, сумма гауссовской СВ и СВ, подчиняющейся МПРВ Вейбулла нормализуется. При этом наличие сигнальной составляющей приводит к появлению ненулевого положительного математического ожидания (МО) в ПРВ. Отличия в графиках в основном касаются МО СВ, которые увеличиваются с ростом ![]() .
.
Формально постановка и решение задачи обнаружения сигнала с амплитудой, распределенной по закону Вейбулла, и равномерно распределенной фазой на фоне гауссовской помехи точно такая же, как и в гауссовском случае. Разница состоит лишь в том, как распределены помехи и шум. Наибольший интерес для практики представляет случай, когда помехи
и шум, или только шум, распределены по гауссовскому закону. В случае коррелированных выборок ![]() это означает, что по каждой из проверяемых гипотез ПРВ будет иметь вид:
это означает, что по каждой из проверяемых гипотез ПРВ будет иметь вид:
.gif) (7)
(7)где ![]() ,
, .gif) ;
;
![]() - соответствует математическому ожиданию от соответствующего вектора
- соответствует математическому ожиданию от соответствующего вектора ![]() ;
;
![]() - ковариационная матрица вектора
- ковариационная матрица вектора ![]() .
.
Таким образом, для фиксированного ![]() можно считать, что векторы условного математического ожидания по гипотезам
можно считать, что векторы условного математического ожидания по гипотезам ![]() и
и ![]() равны
равны ![]() и
и ![]() и соответствующие ковариационные матрицы определяются выражениями
и соответствующие ковариационные матрицы определяются выражениями ![]() и
и ![]() .
.
Используя представление экспоненты под интегралом по параметрам ![]()
в виде степенного ряда и ограничивая количество членов конечным числом L, приводим (7) к более удобному виду. С учетом вышесказанного логарифм отношения правдоподобия будет равен:
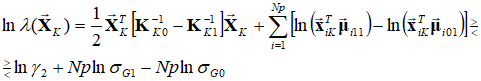 (8)
(8)где .gif) ,
, ![]() .
.
Аналогичный вид имеет и ![]() , но с учетом того, что вместо
, но с учетом того, что вместо ![]() используется
используется ![]() , а вместо
, а вместо ![]() подставляется
подставляется ![]() .
.
На рисунке 2 представлен один из вариантов реализации схемы, реализующей задачу совместного обнаружения и оценивания прямого сигнала, принимаемого при наличии многолучевого распространения и помех.
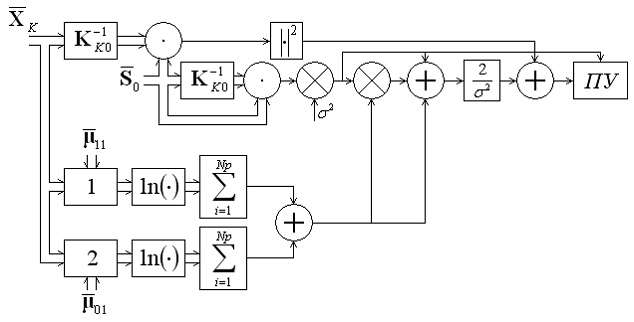
Рис. 2. Вариант реализации схемы, реализующей задачу совместного
обнаружения и оценивания прямого сигнала, принимаемого
при наличии многолучевого распространения и помех
На рисунке 2 в блоке 1 выполняется вычисление компонентов ![]() .
.
В блоке 2 производится вычисление компонентов ![]() . Заметим, что реализация блоков 1 и 2 может осуществляться в различных вариантах, рассмотрение которых выходит за рамки работы.
. Заметим, что реализация блоков 1 и 2 может осуществляться в различных вариантах, рассмотрение которых выходит за рамки работы.
Поскольку ![]() имеет ненулевой вектор МО, реализация отличается от известных схем [1,2], используемых для обработки гауссовских сигналов, наличием нижней ветви схемы, реализующей второе слагаемое в (8).
имеет ненулевой вектор МО, реализация отличается от известных схем [1,2], используемых для обработки гауссовских сигналов, наличием нижней ветви схемы, реализующей второе слагаемое в (8).
Следует отметить, что схемы, подобные изображенной на рисунке 2, будут использоваться и для обработки сигналов с амплитудой, распределенной по логарифмически нормальному и m (Накагами) законам распределения вероятностей. Отличия будут только в величинах ![]() и
и ![]() .
.
Таким образом в статье была сформулирована и решена задача совместного обнаружения и оценивания прямого сигнала, принимаемого при наличии многолучевого распространения и помех в случаях, когда амплитуда распределена по логарифмически нормальному, Вейбулловскому и ![]() (Накагами) законам распределения вероятностей. Для решения указанной задачи были разработаны аналитические выражения для многомерных плотностей распределения вероятностей случайного процесса сигнала в случаях, когда амплитуда имеет распределение одного из трех указанных выше типов. Был представлен вариант реализации схемы, реализующей задачу совместного обнаружения и оценивания прямого сигнала, принимаемого при наличии многолучевого распространения и помех.
(Накагами) законам распределения вероятностей. Для решения указанной задачи были разработаны аналитические выражения для многомерных плотностей распределения вероятностей случайного процесса сигнала в случаях, когда амплитуда имеет распределение одного из трех указанных выше типов. Был представлен вариант реализации схемы, реализующей задачу совместного обнаружения и оценивания прямого сигнала, принимаемого при наличии многолучевого распространения и помех.
Библиографический список
- Ван Трис, Г. Теория обнаружения, оценок и модуляции. т.3. Обработка сигналов в радио и гидролокации и прием случайных гауссовых сигналов на фоне помех / Г.Ван Трис; пер. с англ. под ред. В.Т. Горяинова. – М.: Сов. радио, 1977. – 664 с.
- Обработка сигналов в многоканальных РЛС / А.П.Лукошкин, С.С. Каринский, А.А.Шаталов и др. Под ред. А.П.Лукошкина. – М.: Радио и связь, 1983. – 328 с.
- Barton D.K. Radar multipath theory and experimental data. “IEEE Radar-77. London, England, Oct.25-28, 1977, pp.308-312.
- Farina A., Russo A. Scanapieco F. Radar detection of target signals in non Gaussian clutter: theory and application. IEEE Proceedings-F. Radar and Signal processing. Vol 137, Part F, №1, Febryary 1990, p 92-99.
- Авдяков В.А. Статистические характеристики узкополосных сигналов с амплитудой, распределенной по закону Вейбулла, принимаемых от низколетящих целей/ В.А. Авдяков, А.С. Бачевский, Э.В. Власов, В.А. Шаталова. Радиоэлектроника интеллектуальных транспортных систем. Научно-технический сборник трудов, выпуск №1, СЗТУ, 2009, с.98.
