Научный руководитель: Токарев Кирилл Евгеньевич
Введение
Многие читатели данной статьи наверняка знают игру «Мемори», где игрокам нужно разгадывать пары одинаковых картинок на карточках. В ходе написания электронной версии игры «Мемори» на языке C#, рассчитанной на двух участников, возникла проблема: а кто из игроков должен иметь возможность совершить первый ход? Чтобы игра была наиболее честной, теоретическая вероятность победы игрока, победившего в предыдущей партии, должна быть ниже, чем теоретическая вероятность победы проигравшего игрока (если партия первая, то не важно, кто ходит первым). А теоретическая вероятность победы напрямую зависит от того, первым игрок сходил или нет. Моя задача – определить эту вероятность, чтобы в зависимости от неё решать, какому из игроков давать возможность совершить первый ход.
Для расчёта вероятности требуется написать программу, которая моделирует все возможные исходы игрового процесса и определяет вероятности победы у каждого из игроков, а также вероятность ничьи. Так как программа должна вычислять теоретические вероятности, то будем считать, что игроки – это роботы с идеальной памятью, помнящие всё расположение известных ранее картинок и совершающие ходы по строго заданному алгоритму.
Описание математической модели
В ходе проектирования и программной реализации определителя вероятностей реализована математическая модель, суть которой заключается в следующем:
Имеются два игрока: «А» и «В». Пусть игрок А – игрок, сделавший первый ход.
Так как порядок картинок для данной задачи не важен, расположить их можно в любом порядке. Я расположил картинки следующим образом, заменив их на соответствующие им цвета (рис. 2).

Рисунок 2 – Замена картинок на соответствующие цвета
Каждый из игроков должен запоминать, какие картинки были на ранее открываемых ячейках, чтобы иметь возможность совершить заведомо правильный ход или увеличить вероятность совершения правильного хода. Поскольку оба игрока видят одно и то же поле, то и знания о ячейках у них одинаковые.
Для организации хранения игровых ситуаций и работы с ними используется класс, который содержит:
1) массив ячеек, каждая из которых может быть:
а) неизвестной;
б) известной;
в) открытой игроком А;
г) открытой игроком В;
2) информация о том, чей сейчас ход;
3) вероятность достижения данной игровой ситуации.
На рисунке 3 изображён пример игровой ситуации.

Рисунок 3 – Пример игровой ситуации
Известные ячейки имеют цветную штриховку, открытые ячейки – сплошной цвет и имя открывшего их игрока, а неизвестные ячейки – полностью белые.
Структура игрового процесса
Для анализа возможных игровых ситуаций и определения вероятностей их выпадения будет удобно рассмотреть игровой процесс на следующем примере игры:
1. В начале игры все ячейки являются неизвестными (рис. 4).

Рисунок 4 – Изначальная игровая ситуация
Первым ходит игрок А. Он может открыть любые две ячейки на поле. Однако если рассматривать все возможные сочетания из 16 элементов по 2, то количество последующих рассматриваемых ситуаций будет расти в геометрической прогрессии. Чтобы избежать этого, рассматриваться должны только стратегически разные ситуации, то есть, ситуации, которые отличаются друг от друга только влиянием на дальнейший игровой процесс.
Для удобства анализа игровых ситуаций и для большей наглядности роботы программируются так, что, в случае предстоящего выбора случайной ячейки, роботы выбирают ближайшую к верхнему левому краю ячейку в диапазоне выбираемых.
2. Игрок А открывает случайно выбранную ячейку (рис. 5).

Рисунок 5 – Первое открытие ячейки
3. Затем игрок А открывает другую случайно выбранную ячейку, после чего возможны две стратегически разные ситуации:
1) Игрок А отгадал пару (событие C) (рис. 6);
2) Игрок А не отгадал пару (событие E) (рис. 7).

Рисунок 6 – Отгадывание пары на первом ходе
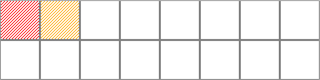
Рисунок 7 – Не отгадывание пары на первом ходе
В случае если игрок не отгадал пару, ячейки закрываются, но роботы уже знают, какие картинки находятся в этих ячейках.
Найдём вероятности событий C и E, они же вероятности возникновения двух ранее рассмотренных ситуаций.
P(C) = 1 / ([количество ячеек] – 1) = 1/15.
P(E) = 1 – P(C) = 14/15.
Если игрок А не отгадал пару, то следующим ходит игрок В.
3. Допустим, игрок А не отгадал пару на первом ходе, оставив за собой «следы» на поле (рис. 7).
Игрок В не видит здесь возможного заведомо правильного хода, поэтому начинает свой ход с открытия случайно выбранной ячейки с неизвестной картинкой. Игрок В открывает одну из 14 неизвестных ячеек. Однако здесь имеет смысл то, какую именно ячейку откроет игрок В, так как он имеет знания о картинках в двух ранее открываемых ячейках и способен их применить в случае, если картинка на только что открытой ячейке встречалась ранее (рис. 8).
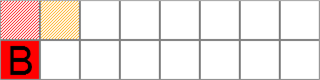
Рисунок 8 – Возможность применения знаний о предыдущих ячейках
4.1. В таком случае игрок В отгадывает пару, так как он помнит, где находится необходимая пара (событие B) (рис. 9).
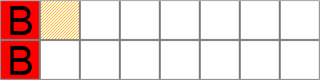
Рисунок 9 – Применение знаний о предыдущих ячейках
Вероятность события B: P(B) = 2/14.
4.2. Но игроку В может и не повезти, если только что открытая ячейка содержит картинку, которую игрок видит первый раз (рис. 10).
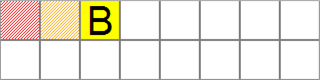
Рисунок 10 – Открытие ячейки с неизвестной картинкой
В таком случае игрок открывает ещё одну случайно выбранную ячейку из оставшихся 13-ти неизвестных. Здесь возможны следующие три стратегически разные ситуации:
1) Игрок В отгадал пару (событие C) (рис. 11);
2) Игрок В не отгадал пару, у игрока А появляется возможный заведомо правильный ход
(событие D) (рис. 12);
3) Игрок В не отгадал пару, у игрока А не появляется возможный заведомо правильный ход (событие E) (рис. 13).
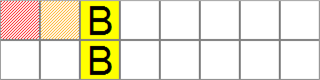
Рисунок 11 – Отгадывание пары ранее неизвестных ячеек
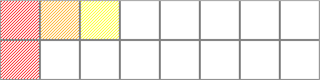
Рисунок 12 – Неотгадывание пары с появлением заведомо правильного хода у соперника

Рисунок 13 – Неотгадывание пары без появления заведомо правильного хода у соперника
Следует понимать, что эти 3 ситуации могут произойти, только если первая открытая ячейка содержит неизвестную ранее картинку. Поэтому для расчёта вероятностей этих событий воспользуемся формулой расчёта условных вероятностей [1].
PB’(C) = 12/14 * 1/13.
PB’(D) = 12/14 * 2/13.
PB’(E) = 12/14 * 10/13.
5. Допустим, происходит событие D, у игрока А появляется возможность совершить заведомо правильный ход, и он просто открывает две ячейки с известными ранее картинками (событие А) (рис. 14).
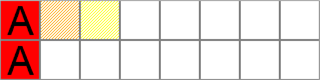
Рисунок 14 – Совершение заведомо правильного хода
В зависимости от отгадывания пары картинок будет решаться, кто ходит следующим. Открытые (разгаданные) ячейки не рассматриваются игроками.
Чтобы программа вычисления вероятностей обрабатывала все возможные игровые ситуации, она должна содержать рекурсивную функцию, которая по некоторой входной ситуации порождает до 5 новых игровых ситуаций, которые соответствуют ранее упомянутым событиям A, B, C, D, E.
Также, эта функция должна распознавать завершённость игры и вычислять вероятности событий A-E по данной игровой ситуации. Если вероятность какого-либо события равна нулю, то соответствующая ситуация не порождается.
В порождаемых игровых ситуациях меняются следующие свойства:
1) статусы ячеек (совершение хода);
2) активный игрок (A или B);
3) вероятность выпадения (текущая вероятность, умноженная на вычисленную вероятность по формуле для данного события [2]).
Каждая из порождённых игровых ситуаций идёт на обработку этой же рекурсивной функцией.
События A-E означают следующее:
A: Совершение заведомо правильного хода;
B: Отгадывание пары с использованием знания о второй ячейке с попавшейся картинкой;
C: Отгадывание пары ранее неизвестных ячеек;
D: Не отгадывание с появлением заведомо правильного хода у соперника;
E: Не отгадывание без появления заведомо правильного хода у соперника.
В таблице 1 изображено два варианта попавшихся ситуаций, отличающихся друг от друга наличием заведомо правильного хода, и пять новых порождаемых ситуаций с указанием вероятностей их выпадения. В формулах вероятностей количества известных и неизвестных ячеек подписаны соответственно как unknown и known. Для примера правильные ходы показаны как принадлежащие игроку А, хотя это может быть любой игрок.
Для примера без заведомо правильного хода: unknown = 6; known = 2.
Таблица 1 – Обработка игровых ситуаций с расчётом вероятностей порождаемых ситуаций
| Пример попавшейся ситуации (в реальной игре такие ситуации невозможны. Они приведены лишь в качестве примера) |
|
|
| Имеется ли заведомо правильный ход |
Да |
Нет |
| Порождаемые ситуации |
P(A) = 1
|
P(B) = known / unknown
|
|
P(C) = (1 – known / unknown) * (1 / (unknown – 1))
|
||
|
P(D) = (1 – known / unknown) * (known / (unknown – 1))
|
||
|
P(E) = (1 – known / unknown) * ((unknown – known – 2) / (unknown – 1))
|
Проверка вероятности достоверного события [3] как суммы вероятностей порождаемых ситуаций приведена на рисунке 777.
| Доказать, чтоP(B) + P(C) + P(D) + P(E) = 1.Доказательство:
known / unknown + (1 – known / unknown) * (1 / (unknown – 1)) + (1 – known / unknown) * (known / (unknown – 1)) + (1 – known / unknown) * ((unknown – known – 2) / (unknown – 1)) = = known / unknown + (1 – known / unknown) * (1 / (unknown – 1) + known / (unknown – 1) + (unknown – known – 2) / (unknown – 1)) = = known / unknown + (1 – known / unknown) * (1 + known + unknown – known – 2) / (unknown – 1) = = known / unknown + (1 – known / unknown) * (unknown – 1) / (unknown – 1) = = known / unknown + (1 – known / unknown) * 1 = 1, что и требовалось доказать. Проверка выполнена. |
Рисунок 777 – Проверка суммы вероятностей
Особые случаи
1) Попавшаяся ситуация не имеет пар неизвестных ячеек (рис. 15).

Рисунок 15 – Отсутствие пар неизвестных ячеек с одинаковыми картинками
Здесь unknown – known = 0, поэтому вероятности P(C) = P(D) = P(E) = 0, из-за чего соответствующие ситуации не порождаются. Порождается только одна ситуация, соответствующая событию B.
2) Попавшаяся ситуация не имеет известных ячеек (рис. 16).

Рисунок 16 – Отсутствие известных ячеек
Здесь known = 0, поэтому порождаются только две ситуации, соответствующие событиям C и E.
Однако событие E тоже не всегда имеет ненулевую вероятность, поскольку возможен третий особый случай…
3) Количество столбцов неизвестных ячеек равно 1 (рис. 17).
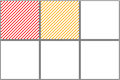
Рисунок 17 – Отсутствие неправильного хода, не влекущего за собой появление заведомо правильного хода у соперника
Здесь невозможно не отгадать пару таким образом, чтобы у соперника не появился заведомо правильный ход, поэтому не порождается ситуация, соответствующая событию E.
На данном этапе алгоритм рекурсивной функции, обрабатывающей игровую ситуацию, таков:
1) если ситуация завершённая, то (…)
2) иначе
2.1) если удалось определить заведомо правильный ход, то совершить этот ход и породить новую игровую ситуацию (событие А)
2.2) иначе породить до 4 игровых ситуаций в зависимости от их вероятностей (события B-E)
Оптимизация вычислений
Ради упрощения анализа игровой ситуации и подсчёта известных и неизвестных ячеек [4] можно рассматривать поле как совокупность столбцов, каждый из которых может являться одним из типов, представленных на рисунке 18.
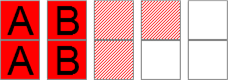
Рисунок 18 – Пять типов столбцов на игровом поле
Всю обработку игровой ситуации можно свести к подсчёту количеств таких типов столбцов, по результатам которого можно сразу же определить и завершённость игры (все столбцы являются столбцами разгаданных ячеек), и количество известных и неизвестных ячеек, а также наличие особых случаев. Это всё рассчитывается за один проход цикла по всем ячейкам игровой ситуации.
Определение победителя
При каждом порождении новой возникающей игровой ситуации, первым делом определяется завершённость игры. Для этого подсчитывается количество столбцов, открытых игроками А и В соответственно. Если эти количества в сумме равны общему количеству столбцов на поле, то ситуация считается завершённой, и победитель определяется по соотношению количеств столбцов, открытых игроками А и В.
Примеры завершённых игровых ситуаций изображены на рисунках 19 и 20.

Рисунок 19 – Пример завершённой игры с победой игрока А

Рисунок 20 – Пример ничьи
Подсчёт вероятностей
Для подсчёта вероятностей было введено 3 глобальных счётчика вероятностей победы каждого из игроков, а также вероятность выпадения ничьи. В процессе игры эти счётчики будут увеличиваться.
Если ситуация завершённая, то вероятность такой ситуации прибавляется к глобальному счётчику вероятности одного из игроков в зависимости от того, кто победил, или к вероятности ничьи [5].
Итоговый алгоритм функции, обрабатывающей игровую ситуацию
1) посчитать количество столбцов следующих 5-ти типов:
а) обе ячейки открыты игроком A;
b) обе ячейки открыты игроком B;
c) обе ячейки содержат известные картинки;
d) одна ячейка содержит известную картинку, а другая – неизвестную;
e) обе ячейки содержат неизвестные картинки
2) если ситуация завершённая, то
2.1) определить победителя или ничью
2.2) добавить шанс текущей ситуации к одному из глобальных счётчиков шансов
3) Иначе
3.1) если удалось определить заведомо правильный ход, то совершить этот ход и породить новую игровую ситуацию (событие А)
3.2) иначе породить до 4 игровых ситуаций в зависимости от их вероятностей (события B-E)
Модификация программы для вычисления вероятностей победы N-ного количества игроков
Так как в игре может быть и более 2 участников, требуется модифицировать определитель вероятностей таким образом, чтобы он вычислял вероятности для каждого из N игроков.
Для этого в классе, хранящего игровую ситуацию, потребовалось изменить формат хранения информации о том, чей сейчас ход, а также убрать типы ячеек, открытых игроками А и В, заменив их на тип «просто открытая ячейка». Теперь очки игроков будут храниться в отдельном массиве из N целых чисел, а номер игрока-победителя будет определяться по максимальному количеству очков в этом массиве с тем условием, что эти очки встречаются в массиве не более одного раза. Если существует несколько победителей с равными максимальными очками, то считается, что игра закончилась ничьёй.
Заключение
Определитель вероятностей возможных исходов игры «Мемори» был реализован при помощи построенной математической модели и выведенных в процессе анализа алгоритмов. Требуемые теоретические вероятности выигрыша игроков и теоретическая вероятность ничьи были вычислены и получены для игры с двумя участниками и полем, состоящим из 16 ячеек. Также были получены результаты для полей других размеров. Выше описанная модификация программы позволила вычислить вероятности исходов игры для разного количества игроков.
В будущем планируется интегрирование данного определителя вероятностей в саму игру, чтобы игроки получали информацию о том, насколько им повезло или не повезло в той или иной степени.
Библиографический список
- Гмурман, В.Е. Теория вероятностей и математическая статистика: Учебник для прикладного бакалавриата / В.Е. Гмурман. – Люберцы: Юрайт, 2016. – 479 c.
- Гмурман, В.Е. Теория вероятностей и математическая статистика: Учебное пособие для бакалавров / В.Е. Гмурман. – М.: Юрайт, 2013. – 479 c.
- Гмурман, В.Е. Теория вероятностей и математическая статистика: Учебник для СПО / В.Е. Гмурман. – Люберцы: Юрайт, 2016. – 479 c.
- Колесников А. П. Методы численного анализа, изложенные на языке формул и алгоритмическом языке C#; Высшая школа – Москва, 2017. – 414 c.
- Культин Никита Основы программирования в Microsoft Visual C# 2010; БХВ-Петербург – М., 2011. – 634 c.







