НОВЫЙ ВАРИАНТ ДОКАЗАТЕЛЬСТВА АКСИОМЫ О ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ, ИЛИ ПЯТОГО ПОСТУЛАТА ЕВКЛИДА

 Скачать статью в формате PDF

Доказательство аксиомы о параллельных прямых, или пятого постулата Евклида, было дано в статье автора, опубликованной ранее в данном журнале: Плисова Н.Н. Доказательство аксиомы о параллельных прямых, или пятого пос­тулата Евклида // Современные научные исследования и инновации, 2019, № 7 [Электронный ресурс]. В приведенном в указанной статье доказательстве в рамках классической геометрии определялась сумма углов в треугольнике и применялась оригинальная теорема о равенстве угла между пересекающимися прямыми углу между перпендикулярными им прямыми. В новом варианте доказательства сумма углов в треугольнике и указанная теорема не используются. Новое доказательство аксиомы о параллельных прямых в рамках классической геометрии основано на доказательстве совпадения восставленного к прямой и опущенного на прямую перпендикуляров. Новый вариант доказательства базируется на аксиоматике планиметрии, уже приведенной в указанной статье автора и не приводимой заново в данной статье.

Постановка задачи
Теорема: Через любую точку, не лежащую на данной прямой, на плоскости проходит прямая, параллельная данной, и притом только одна (Ax. 2.13.).
Дано: прямая а; точка В, не лежащая на прямой а.
Задача: Доказать, что через точку В проходит единственная прямая b, параллельная прямой а.

Доказательство:
1. Построение перпендикуляра, опущенного из данной точки на данную прямую
Задача: Провести прямую, проходящую через точку В и перпендикулярную прямой а.
Построение: Опустить перпендикуляр из точки В на прямую а значит провести через точку В серединный перпендикуляр к отрезку на прямой а (Def. 3.10.).
Проводим дугу окружности с центром в точке В и некоторым радиусом r так, чтобы она пересекла прямую а в двух точках (Ax. 5.1., 5.2.3.); обозначаем точки пересечения через С и М (Рис. 1).
Проводим окружность с центром в точке С и радиусом СВ, которая проходит через точку В (Ax. 5.2.1.). Проводим окружность с центром в точке М и радиусом МВ=СВ, которая проходит через точку В и пересекается с предыдущей окружностью (Ax. 5.10.); точку пересечения окружностей в другой по отношению к точке В полуплоскости, образуемой прямой а, обозначаем через В₁.

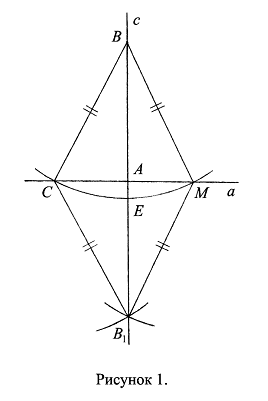
Проводим через точки В и В₁ прямую и обозначаем ее через с (Ax. 2.2.); обозначаем точку пересечения прямой с с прямой а через А (Def. 2.7.); обозначаем точку пересечения прямой с с дугой через Е (Ax. 5.1.).
Нужно доказать, что прямая с перпендикулярна прямой а. Радиусы окружностей равны: , следовательно,  по трем сторонам (Ax. 8.5.3.), следовательно, по аксиоме о равенстве фигур (Ax. 6.8.): , значит, , так как величина угла не зависит от длины его сторон. Отсюда следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит,  (Ax. 6.8.); эти углы – смежные (Def. 4.15.), то есть: , следовательно, , то есть эти углы – прямые (Def. 4.10.); это значит, что прямая с перпендикулярна прямой а (Def. 2.10).
Из независимости величины угла от того, какая из его сторон считается первой, а какая второй, следует, что если прямая с перпендикулярна прямой а, то и прямая а перпендикулярна прямой с, то есть свойство перпендикулярности прямых взаимно; при этом независимость величины угла от порядка рассмотрения его сторон следует из независимости длины отрезка от того, от какого его конца она измеряется, так как угол, равный данному, строится как треугольник, равный данному по трем сторонам (Ax. 8.5.3.); независимость длины отрезка от порядка выбора его концов является эмпирическим свойством циркуля как инструмента, которым измеряется расстояние.


На прямую а из точки В опущен перпендикуляр с.
2. Доказательство единственности перпендикуляра, опущенного из данной точки на данную прямуюЗадача: Доказать, что прямая с, проходящая через точку В, не лежащую на прямой а, и перпендикулярная прямой а (п. 1.), единственна.
Доказательство: Предположим, что прямая с не единственна и существует прямая с₁, отлич­ная от прямой с, которая проходит через точку В и перпендикулярна прямой а. Это значит, что прямая с₁ проходит через точку В и не проходит через точку А (Ax. 2.6.); обозна­чаем точку пересечения прямых с₁ и а через А₁. Проводим дугу окружности с центром в точке В и радиусом ВА₁, пересекающую прямую с (Ax. 5.1., 5.4.2.); обозначаем точку пересе­чения дуги и прямой с через К (Рис. 2). Проводим дугу окружности с центром в точке В и радиусом ВА до пересечения ее с прямой с₁; обозначаем точку пересечения через L (Ax. 9.5.).
, то есть наклонная длиннее перпендикуляра.
,
,
то есть  не является кратчайшим отрезком между точкой В и прямой а; значит, прямая с₁ является наклонной к прямой а, а не перпендикуляром к ней, что противоречит сделанному предположению об их перпендикулярности. Предположение о том, что прямая с₁, отличная от прямой с, перпендикулярна прямой а, приводит к противоречию, значит, оно неверно. Следовательно, перпендикуляр с, опущенный из точки В на прямую а, единствен, что и требовалось доказать.

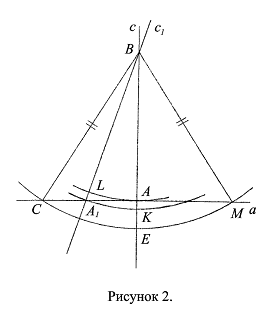
Аксиома о единственности перпендикуляра, опущенного из данной точки на данную прямую (Ax. 2.12.), доказана.

3. Построение перпендикуляра, восставленного к первому перпендикуляру
Задача: Восставить перпендикуляр из точки В, лежащей на прямой с, к прямой с (п. 1.).
Построение (Рис. 3): Проводим окружность с центром в точке В и радиусом ВА, пересекающуюся с прямой с в точке А и второй точке, которую обозначаем через Р (Ax. 5.3.); при этом ВА=ВР (Def. 1.13.). Проводим окружность с центром в точке А и радиусом АР=2ВА (Def. 1.14.); проводим окружность с центром в точке Р и радиусом РА=АР, пересекающуюся с предыдущей (Ax. 5.10.); обозначаем точки пересечения окружностей через О и Q. Через точки О и В проводим прямую и обозначаем ее через b (Ax. 2.2.).
Нужно доказать, что прямая b перпендикулярна прямой с. Радиусы окружности с центром в точке А: АО=АР и окружности с центром в точке Р: РО=РА=АР равны: АО=РО, при том что ВА=ВР. Следовательно,  по трем сторонам (Ax. 8.5.3.), значит,  по аксиоме о равенстве фигур (Ax. 6.8.); эти углы являются смежными (Def. 4.15.), то есть: , следовательно, , то есть эти углы являются прямыми (Def. 4.10.). Прямая b является серединным перпендикуляром к отрезку РА (Def. 3.10.). Все эти утверждения справедливы и при рассмотрении точки Q вместо точки О. Перпендикулярность прямых b и с (Def. 2.10.) доказана.

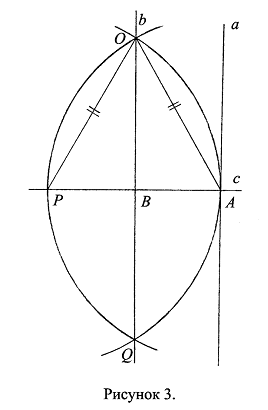
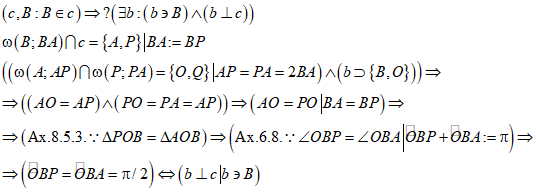
Перпендикуляр b восставлен из точки В к прямой с.
4. Доказательство единственности перпендикуляра, восставленного из данной точки прямой к этой прямой
Задача: Доказать, что перпендикуляр b, восставленный из точки В к прямой с (п. 3.), единствен.
Доказательство: Предположим, что прямая b не единственна и существует прямая b₁, отличная от прямой b и перпендикулярная прямой с.
Так как прямая b₁ отлична от прямой b, то она проходит через точку В, но не проходит через точку О (Ax. 2.6.), то есть не проходит через точку пересечения окружностей с центрами в точках Р и А и радиусами РА и АР. Обозначаем точки пересечения прямой b₁: с окружностью с центром в точке Р и радиусом РА через Т и R, с окружностью с центром в точке А и радиусом АР через S и U (Рис. 4).

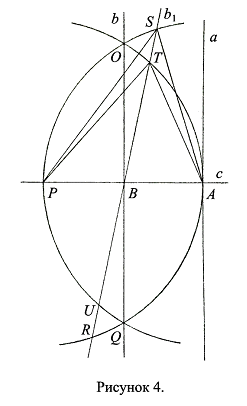
Точка S отлична от точки T, следовательно:
; ; следовательно:
 и ; значит:
 и  (противоречие Ax. 6.9.); следовательно:
 и , иначе для треугольников выполнялось бы равенство по двум сторонам и углу между ними (Ax. 8.5.1.);
 и , так как эти углы смежные (Def. 4.15.), следовательно:
 и ,
то есть прямая b₁ не перпендикулярна прямой с (противоречие Def. 4.10.), что противоречит предположению об их перпендикулярности. Предположение о том, что прямая b не единственна и существует прямая b₁, отличная от прямой b и перпендикулярная прямой с, приводит к противоречию, следовательно, оно неверно. Следовательно, перпендикуляр b, восставленный из точки В к прямой с, единствен, что и требовалось доказать.

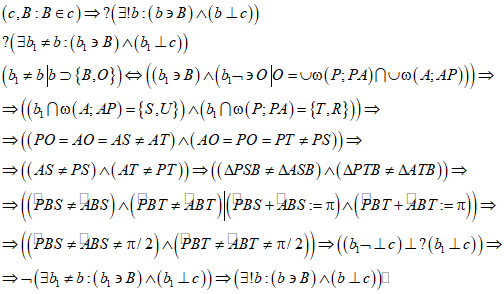
Аксиома о единственности перпендикуляра, восставленного из данной точки прямой к этой прямой (Ax. 2.11.), доказана.

5. Опускание на данную прямую перпендикуляра из точки, принадлежащей восставленному к этой прямой перпендикуляру
Задача: Опустить на прямую с перпендикуляр из точки О, лежащей на прямой b (п. 3.).
Построение: Опустить перпендикуляр из точки О на прямую с значит провести через точку О серединный перпендикуляр к отрезку на прямой с (Def. 3.10.).
Проводим дугу окружности с центром в точке А и радиусом АО в другую полуплос­кость по отношению к точке О, образуемую прямой с. Проводим дугу окружности с цент­ром в точке Р и радиусом РО=АО в другую полуплоскость по отношению к точке О, обра­зу­емую прямой с, которая проходит через точку О и пересекается с дугой предыдущей окружности (Ax. 5.10.); точку пересечения окружностей в другой по отношению к точке О полуплос­кости, образуемой прямой с, обозначаем через Q. Через точки О и Q проводим прямую и обозначаем ее через b₁, точку пересечения прямых b₁ и с обозначаем через N (Рис. 5).
Нужно доказать, что прямая b₁ перпендикулярна прямой с. Радиусы окружностей равны: , следовательно,  по трем сторонам (Ax. 8.5.3.), следовательно, по аксиоме о равенстве фигур (Ax. 6.8.): , значит, . Отсюда следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит,  по аксиоме о равенстве фигур (Ax. 6.8.); эти углы – смежные (Def. 4.15.), то есть: , следовательно, , то есть эти углы – прямые (Def. 4.10.); это значит, что прямая b₁ перпендикулярна прямой c (Def. 2.10.).
На прямую с опущен перпендикуляр b₁ из точки О, принадлежащей восставленному к прямой с перпендикуляру b.

6. Доказательство теоремы о совпадении перпендикуляра, восставленного из данной точки данной прямой к этой прямой, и перпендикуляра, опущенного на данную прямую из точки, принадлежащей восставленному к ней перпендикуляру
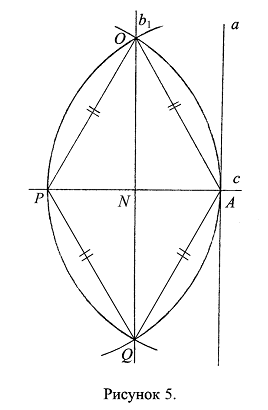
Задача: Доказать, что перпендикуляр b₁, опущенный на прямую с из точки О, принадлежащей прямой b, являющейся перпендикуляром, восставленным к прямой с из точки В, лежащей на прямой с, совпадает с прямой b.
Доказательство: Из п. 5 следует, что  по двум сторонам и углу между ними (Ax. 8.5.1.); значит, по аксиоме о равенстве фигур (Ax. 6.8.): PN=NA. Предполагалось, что прямая b₁ может не проходить через точку В, а пересекается с прямой с в точке N (Рис. 6). В п. 3. было установлено, что PB=BA. Из предположения о том, что точка N отлична от точки В, следует, что:  и , следовательно, при определении длины отрезка РА в пунктах 3. и 5. возникает противоречие:
 .
Предположение о том, что прямая b₁, являющаяся опущенным на прямую с перпендикуляром, не совпадает с прямой b, являющейся восставленным к прямой с перпендикуляром, приводит к противоречию, следовательно, оно неверно. Следовательно, перпендикуляр b₁, опущенный на прямую с из точки О, принадлежащей перпендикуляру b, восставленному к прямой с из точки В, лежащей на прямой с, совпадает с восставленным перпендикуляром b, что и требовалось доказать.

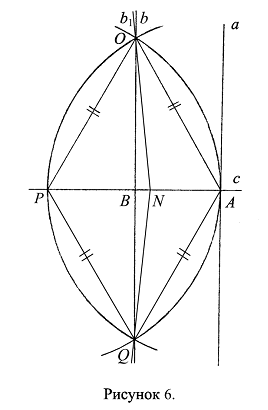
Восставленный и опущенный на прямую а перпендикуляры совпадают и в том случае, когда на прямой а выбирается отрезок, отличный от отрезка PN. Возьмем на прямой b произвольную точку , отличную от точки О, и опустим из точки  перпендикуляр на прямую с, который обозначим через . Перпендикуляр  опус­кается тем же способом, что и перпендикуляр ; доказательство перпендикулярности прямых  и с аналогично доказательству перпендикулярности прямых  и с. Предполо­жим, что прямая  не совпадает с прямой b. Тогда получается, что из точки , лежащей на прямой b, опущены на прямую с сразу два перпендикуляра – b и , что противоречит аксиоме о единственности опущенного перпендикуляра (Ax. 2.12.). Предположение о том, что прямая  не совпадает с прямой b, приводит к противоречию, следовательно, оно невер­но, следовательно, прямая  совпадает с прямой b, то есть прямая b является единственным перпендикуляром к прямой с, проходящим через точку В, что и требовалось доказать.

Этот вывод справедлив и для другой последовательности прове­дения перпендикуляров к прямой а. Если сначала на данную прямую a опускается перпендикуляр b из точки O, не лежащей на прямой а, а затем из точки В – точки пересечения прямой а с опущенным на нее перпендикуляром b – восставляется перпенди­куляр d к прямой а, проходящий через точку D, предположитель­но не лежащую на прямой b (Ax. 2.6.), то развернутый угол, образуе­мый прямой а, будет равен: . Если , то это противоречит предположению о том, что прямые b и d не совпадают; если , то это противоречит определению развернутого угла (Def. 4.11.). Предположение о том, что прямые b и d не совпадают, приводит к противоречию, следовательно, оно неверно, следовательно, прямая d совпадает с прямой b. Прямая b, перпендикулярная прямой a и пересекающаяся с ней в точке В, единственна, что и требовалось доказать.

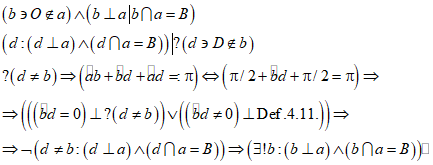
Сформулируем теоремы: 1) Перпендикуляр, восставленный из данной точки данной прямой к этой прямой, и перпендикуляр, опущенный на данную прямую из точки, принадлежащей восставленному к ней перпендикуляру, совпадают. 2) Перпендикуляр, опущенный на данную прямую из точки, не лежащей на этой прямой, и перпендикуляр, восставленный к данной прямой из точки пересечения данной прямой и опущенного на нее перпендикуляра, совпадают. Теоремы доказаны.

7. Доказательство того, что прямая, к которой восставлен перпендикуляр, единственна по отношению к этому перпендикуляру
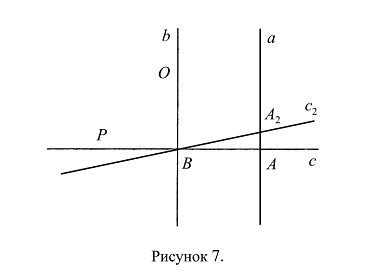
Задача: Доказать, что прямая с – единственный перпендикуляр к прямой b, пересекающийся с прямой b в точке В.
Доказательство: Предположим, что прямая с – не единственный перпендикуляр к прямой b, пересекающийся с ней в точке В, а существует некоторая прямая , отличная от прямой с, которая проходит через точку В и перпендикулярна прямой b. Тогда прямые  и с пересекаются в точке В под некоторым углом; прямая , перпендикулярная прямой b, пересекается с прямой а в точке  (Рис. 7). Угол  – развернутый, следовательно: , или же, . Если , то это противоречит предположению о том, что прямые c и  не совпадают; если , то это противоречит определению развернутого угла (Def. 4.11.). Предположение о том, что прямые с и  не совпадают, приводит к противоречию, следовательно, оно неверно, следовательно, прямая  совпадает с прямой с. Прямая с, перпендикулярная прямой b и пересекающаяся с ней в точке В, единственна, что и требовалось доказать.

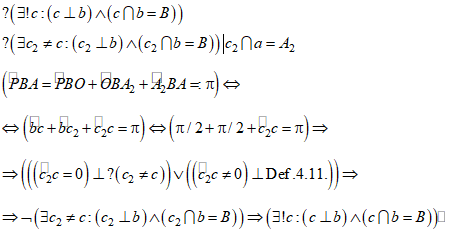
8. Построение перпендикуляра, восставленного к перпендикуляру, опущенному на данную прямую
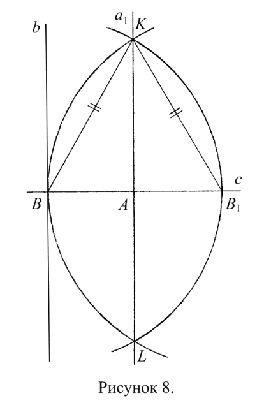
Задача: Восставить из точки А, являющейся точкой пересечения прямых а и с, перпендикуляр к прямой с.
Построение: Проводим окружность с центром в точке А и радиусом АВ, пересекающуюся с прямой с в другой по отношению к точке В полуплоскости, образуемой прямой а (Рис. 8); обозначаем точку пересечения через ;  (Def. 1.13.). Проводим дугу окружности с центром в точке В и радиусом  (Def. 1.14.); проводим дугу окружности с центром в точке  и радиусом , пересекающуюся с предыдущей дугой в двух точках (Ax. 5.10.); обозначаем точки пересечения окружностей через K и L. Через точки А и К проводим прямую и обозначаем ее через  (Ax. 2.2.).
Нужно доказать, что прямая  перпендикулярна прямой с. Радиусы окружностей с центрами в точках В и  равны: , при том что . Следовательно,  по трем сторонам (Ax. 8.5.3.), значит,  по аксиоме о равенстве фигур (Ax. 6.8.); эти углы являются смежными (Def. 4.15.), то есть: , следовательно, , то есть эти углы являются прямыми (Def. 4.10.). Прямая  является серединным перпендикуляром к отрезку , лежащему на прямой с (Def. 3.10.). Перпендикулярность прямых  и с (Def. 2.10.) доказана.

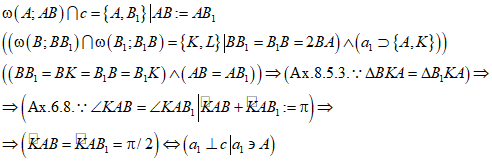
9. Доказательство того, что прямая, на которую опущен перпендикуляр, единственна по отношению к этому перпендикуляру
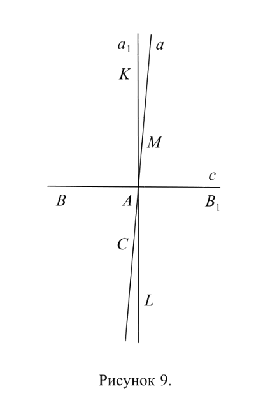
Задача: Доказать, что перпендикуляр , восставленный к прямой с в точке А (п.7.), совпадает с прямой а, то есть данная прямая а является единственной по отношению к перпендикуляру с к ней.
Доказательство: Предположим, что прямая  не совпадает с прямой а, то есть прямые  и а пересекаются в точке А под некоторым углом. Прямая а, перпендикулярная прямой с, проходит через точки А и М; прямая , перпендикулярная прямой с, проходит через точки А и К (Рис. 9). Из п. 1. следует, что ; из п. 8. следует, что ; угол  – развернутый, следовательно: , что равносильно следующему: . Если , то это противоречит предположению о том, что прямые а и  не совпадают; если , то это противоречит определению развернутого угла (Def. 4.11.). Предположение о том, что прямые а и  не совпадают, приводит к противоречию, следовательно, оно неверно, следовательно, прямая  совпадает с прямой а. Прямая а, перпендикулярная прямой с и пересекающаяся с ней в точке А, единственна, что и требовалось доказать.

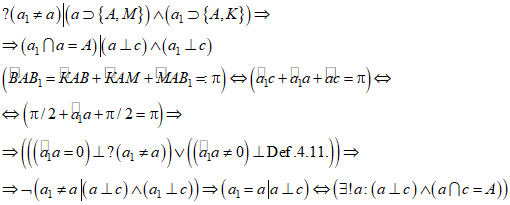
Единственность прямой а, которой перпендикулярна прямая с, пересекающаяся с ней в точке А, доказана. Единственность прямой с, перпендикулярной прямой а и пересекающейся с ней в точке А, доказана в п. 2. Единственность прямой b, перпендикулярной прямой с и пересекающейся с ней в точке В, доказана в пп. 4 и 6. Единственность прямой с, перпендикулярной прямой b и пересекающейся с ней в точке В, доказана в п. 7. Совпадение восставленного и опущенного перпендикуляров доказано в п. 6.
Сформулируем теорему: Если две прямые перпендикулярны, то каждый из этих перпендикуляров является единственным по отношению к другому, вне зависимости от того, восставленные это перпендикуляры или опущенные. Теорема доказана.

10. Доказательство того, что прямая, перпендикулярная перпендикуляру к данной прямой, параллельна данной прямой
Задача: Доказать, что прямая b, проходящая через точку В, не лежащую на прямой а, и перпендикулярная прямой с, которая перпендикулярна прямой а и проходит через точку В, параллельна прямой а.
Доказательство: Предположим, что прямая b не параллельна прямой а; следовательно, прямые а и b пересекаются в некоторой точке D. Прямые а и b являются перпендикулярами, восставленными к прямой с из разных точек А и В (пп. 2., 5.). По теореме о совпадении восставленного и опущенного перпендикуляров (п. 6.), прямые а и b совпадают с опущенными на прямую с перпендикулярами. Получается, что из точки D, общей для прямых а и b, опущены сразу два перпендикуляра на прямую с – прямые а и b, что противоречит аксиоме о единственности опущенного перпендикуляра (Ax. 2.12.). Предположение о том, что из точки D, общей для прямых а и b, опущены сразу два перпендикуляра на прямую с, противоречит аксиоме о единственности опущенного перпендикуляра и теореме о единственности перпендикуляров по отношению друг к другу (п. 9.). Предположение о том, что прямая b не параллельна прямой а, приводит к противоречию, следовательно, оно неверно, следовательно, прямая b параллельна прямой а, что и требовалось доказать.

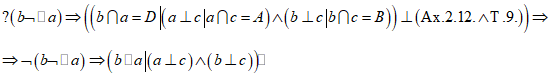
Сформулируем теорему: Если две прямые перпендикулярны одной и той же третьей прямой, то эти прямые параллельны. Теорема доказана.

11. Доказательство единственности прямой, проходящей через точку, не лежащую на данной прямой, и параллельной данной прямой
Задача: Доказать, что прямая b, проходящая через точку В, не лежащую на прямой а, и параллельная прямой а, единственна.
Доказательство: Предположим, что прямая b не единственна и существует прямая b₃, отличная от прямой b, проходящая через точку В и параллельная прямой а. По теореме о единственности перпендикуляров, пересекающихся в данной точке (п. 9.), прямая b₃ не перпендикулярна прямой с, а перпендикулярна прямой , отличной от прямой с. Тогда имеем: прямая а перпендикулярна прямой с, прямая b перпендикулярна той же прямой с, следовательно, по теореме п. 10, эти прямые параллельны; прямая а перпендикулярна прямой с, прямая  перпендикулярна прямой  и не перпендикулярна прямой с, следовательно, теорема о параллельности прямых, перпендикулярных одной и той же прямой (п. 10.), для прямых а и  не выполняется, следовательно, прямые а и  не параллельны, что противоречит предположению об их параллельности. Предположение о том, что прямая b не единственна и существует прямая b₃, отличная от прямой b, проходящая через точку В и параллельная прямой а, приводит к противоречию, следовательно, оно неверно. Следовательно, прямая b проходящая через точку В, не лежащую на прямой а, и параллельная прямой а, единственна, что и требовалось доказать.



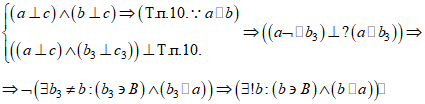
Единственность прямой, проходящей через точку, не лежащую на данной прямой, и параллельной данной прямой, доказана.
Аксиома о параллельных прямых (Ax. 2.13.), или пятый постулат Евклида, доказана.

12. Доказательство единственности параллельных прямых по отношению друг другу
Задача: Доказать единственность данной прямой а, параллельной прямой b.
Доказательство: Предположим, что прямая а – не единственная прямая, параллельная прямой b, следовательно, существует прямая , параллельная прямой b и проходящая через точку А – точку пересечения прямых а и с. Для параллельных прямых  и b должна выполняться теорема об их перпендикулярности одной и той же прямой с. Прямая b перпендикулярна прямой с, с которой пересекается в точке В; прямая  не может быть перпендикулярной прямой с в силу единственности перпендикуляров друг другу (п. 9.), так как в точке А прямой с перпендикулярна прямая а. Следовательно, теорема о параллельности прямых, перпендикулярных одной и той же прямой (п. 10.), для прямых  и b не выполняется, следовательно, прямые  и b не параллельны, что противоречит предположению об их параллельности. Предположение о том, что прямая а не единственна и существует прямая , отличная от прямой а, проходящая через точку А и параллельная прямой b, приводит к противоречию, следовательно, оно неверно. Следовательно, прямая а, проходящая через точку А и параллельная прямой b, проходящей через точку В, не лежащую на прямой а, единственна, что и требовалось доказать.



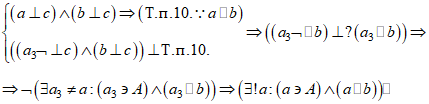
Прямая а, проходящая через точку А и параллельная прямой b, единственна. Прямая b, проходящая через точку В, не лежащую на прямой а, и параллельная прямой а, единственна (п. 11.).
Сформулируем теорему: Параллельные прямые, проходящие через заданные точки плоскости, единственны по отношению друг к другу. Теорема доказана.

Выводы. Доказаны следующие аксиомы и теоремы:
Аксиома о единственности перпендикуляра, опущенного на прямую (п. 2.);
Аксиома о единственности перпендикуляра, восставленного к прямой (п. 4.);
Теорема о совпадении восставленного и опущенного перпендикуляров (п. 6.);
Теорема о единственности перпендикуляров по отношению друг к другу (п. 9.)Теорема о параллельности прямых, перпендикулярных одной и той же третьей прямой (п. 10.);Аксиома о параллельных прямых, или пятый постулат Евклида (п. 11.)
Теорема о единственности параллельных прямых по отношению друг к другу (п. 12.);

1. Плисова Н.Н. Доказательство аксиомы о параллельных прямых, или пятого пос­тулата Евклида // Современные научные исследования и инновации, 2019, № 7 [Электронный ресурс].
2. Энциклопедия элементарной математики. Книга четвертая. Геометрия. – М.: Гос. изд-во физико-математической литературы, 1963. – 568 с.
3. Погорелов А.В. Геометрия. Учебное пособие для 6-10 классов средней школы. – М.: Просвещение, 1980. – 288 с.
4. «Начала» Евклида. Книги I-VI. – М.-Л.: ОГИЗ, Гос. изд-во технико-теоретической литературы, 1948. – 447 с. – (Классики естествознания).
5. Аксиома параллельности Евклида // Материал из Википедии – свободной энциклопедии. URL: https://ru.wikipedia.org/wiki/%D0%90%D0%BA%D1%81%D0%B8%D0%BE%D0.. (дата обращения: 3.09.2018).
6. Аргунов Б.И., Бланк М.Д. Геометрические построения на плоскости. – М.: Гос. учебно-педагогическое изд-во Мин. просвещения РСФСР, 1957. – 267 с.
7. Выгодский М.Я. Справочник по элементарной математике. – М.-Л.: Гос. изд-во технико-теоретической лит-ры, 1950. – С. 274.
8. Таблица математических символов // Материал из Википедии – свободной энциклопедии. URL: https://ru.wikipedia.org/w/index.php?title=Таблица_математических_символов&oldid=98096487 (дата обращения: 13.02.2019).
9. Игошин В.И. Математическая логика: Учебное пособие. – М.: ИНФРА-М, 2016. – 399 с. – (Высшее образование).

Все статьи автора «Плисова Ника Николаевна»