На сегодняшний день проблемы активизации, оптимизации, результативности учебно-познавательной деятельности студентов учреждений профессионального образования являются одними из центральных проблем современной педагогики профессионального образования, а разработка новых технологий профессионально-ориентированного обучения рассматривается как приоритетное направление педагогических и предметно-методических исследований.
Всем известная технологии учебного диалога рассматриваются не только как особая организационная форма процесса учебно-профессионального взаимодействия в системе «преподаватель – обучающийся – группа обучающихся», но и как фактор актуализации критической и рефлексивной функции личности. Опыт диалогического учебно-профессионального общения накапливается постепенно (как у студентов, так и у преподавателя).
Введение в ситуацию учебного диалога предполагает:
а) готовность обучающихся к диалогическому общению (наличие коммуникативного опыта в ситуации диалога и полилога, опыта корректной, развернутой аргументации своей позиции, установки на доброжелательное восприятие иных точек зрения; наличие базовых знаний, достаточного объема информации по обсуждаемому вопросу и др.);
б) готовность преподавателя к диалогическому общению с обучающимися (поиск круга вопросов и проблем в сфере профессионального развития, волнующих студентов, благодаря которому может эффективно складываться личностный смысл изучаемого материала; умение перерабатывать учебный материал в систему проблемных профессионально-ориентированных и личностно значимых вопросов и задач; продумывание различных вариантов развития сюжетных линий диалога и др.).
Таким образом, учебный диалог, особенно затрагивающий вопросы профессионально-личностного развития обучающихся, требует серьезных усилий преподавателя по его подготовки, организации, поддержанию атмосферы доброжелательного и открытого взаимодействия, по актуализации и активизации умений участников гибко встраиваться в быстро меняющуюся ситуацию дискурсивного обсуждения проблемы.
Дистанционные образовательные технологии.
Дистанционное обучение – это целенаправленный процесс интерактивной образовательной деятельности на расстоянии между субъектами педагогического процесса с целью самостоятельного овладения знаниями, умениями, навыками и формирования у обучающихся мотивации получения образования в течение всей жизни, основанный на следующих основополагающих принципах:
- интерактивного взаимодействия;
- особой территориальной и временной характеристики учебного процесса; активной самостоятельной учебной деятельности;
- применения инновационных и информационных технологий; развития непрерывного образования.
Указанные принципы дистанционного обучения делают обучаемого активным, самостоятельным, ответственным, практичным, а сама форма дистанционного обучения является удобной по временным, территориальным и прочим характеристикам.
Дистанционное обучение не только способствует выработке у обучаемых навыка самостоятельной работы, но и повышает активность их учебной деятельности.
Например, включение в профессионально ориентированную учебную деятельность данного вида технологий происходит путем трансляции профессионально ориентированных задач, которые помогают студентам понять, суть применения математического аппарата в своей профессиональной деятельности.
Проективные технологии.
В основе проектной технологии лежит умение студента ориентироваться в информационном пространстве и самостоятельно конструировать свои профессионально-прикладные и практико-ориентированные знания. При выполнении проекта деятельность студентов может быть индивидуальной, парной или групповой. Работа выполняется в течение определенного отрезка времени и направлена на решение конкретной учебно-профессиональной проблемы.
Виды проектной деятельности студентов:
- информационно-аналитические проекты (студенты осваивают различные методы получения профессионально-значимой информации и способы ее обработки: анализ международных, отечественных нормативно-правовых, финансово-экономических документов, компьютерных баз данных, научно-методических, монографических литературных источников, интервью со специалистами-практиками, анализ материалов специальных профессиональных журналов; способы презентации профессионально-значимой информации: доклад, публикация, Интернетфорумы и пр.);
- имитационно-игровые проекты (студенты в группах разрабатывают содержание и сценарий проведения деловой игры, предполагавшей распределение ролей конкретной профессиональной ситуации и др.);
- специализированные практико-ориентированные проекты (результат проекта – обоснование, разработка плана реализации конкретного социального проекта, например, системный анализ инвестиционной стратегии в конкретном регионе, а также обязательное получение внешней экспертной оценки проекта специалистами-практиками).
Умение организовать проектную деятельность студентов – показатель высокой квалификации преподавателя, его способности использовать развивающие технологии профессионально-ориентированного обучения.
Таким образом, проектные технологии формируют осмысленное развитие профессионально-исследовательского интеллекта, а также и целесообразное проектирование практических действий будущего специалиста в сфере выполнения профессионально-ориентированного учебно-познавательного задания.
Технологии модульного обучения.
Под модульным обучением понимается способ организации учебного процесса на основе блочно-модульного представления учебной информации, которому присущи следующие принципы:
- модульность;
- динамичность;
- гибкость;
- паритетность;
- научное изложение материала с максимальным использованием математической символики;
- краткость изложения, не теряющая логического построения теоретического материала;
- наглядность (использование рисунков, чертежей, схем, диаграмм, компьютерной графики и т.д.);
- алгоритмизация учебной деятельности с помощью изучения теоретического материала укрупненными блоками;
- поуровневая индивидуализация учебной деятельности, что создает у студента ситуацию выбора;
- системность и целостность блоков, что способствует экономии времени и быстрому воспроизведению в памяти студентов;
- обобщение и систематизация знаний, что позволяет студентам самостоятельно решать задачи;
- дифференциация обучения путем разработки заданий различного уровня сложности;
- осознанная перспектива;
- доступность технологий обучения;
- открытость образовательного процесса;
- новая роль преподавателя.
Следует отметить, модульная технология совпадает с двумя основными тенденциями развития практики и теории педагогических измерений. Первая – это разработка тестов для проведения объективной итоговой аттестации выпускников вузов. Вторая тенденция – использование обучающего потенциала заданий в тестовой форме для организации самоконтроля – самой гуманной формы контроля знаний.
Модуль — это функциональный целевой узел, в котором учебное содержание и технология овладения им объединены в систему.
Модуль включает в себя:
- законченный блок информации («учебное содержание»);
- целевую программу действий ученика («функциональность»);
- рекомендации (советы) учителя по ее успешной реализации («технология»).
Самое важное в построении модуля — структурирование деятельности ученика по этапам усвоения знаний: восприятие, понимание, осмысление, запоминание, применение, обобщение, систематизация. И здесь большая возможность осуществлять проблемное обучение.
В продолжении проблемного обучения можно отметить следующее, что в курс математического анализа входит множество различных тем. Одним из его разделов является неопределенный интеграл и его применение. Вычисление неопределенного интеграла имеет не только теоретический интерес, к его вычислению сводятся иногда задачи, связанные с практической деятельностью человека. Также понятие неопределенного интеграла широко используется для вычисления инженерно-технических, физических задач. Поэтому в курсе математического анализа изучается тема: «Неопределенный интеграл и его применение».
Существует множество методической (учебники, пособия) и научной литературы (диссертации, статьи, монографии), в которой рассматриваются вопросы, связанные с неопределенным интегралом и методами его нахождения, но зачастую материал в них либо избыточен, либо недостаточен, либо изложен недоступным языком для студента, отсюда проблема «хвостов», «хвостовых сессий» и бесконечных пересдач экзаменов и зачетов.
Следовательно, при изучении данной темы студенты сталкиваются с проблемами необходимости всегда иметь под рукой несколько источников, что крайне неудобно и ограниченности во времени на разбор и изучение данной темы, а преподаватель, в свою очередь, сталкивается с проблемой систематизации и правильности подачи материала.
Одним из решений данного вопроса стало внедрение федеральных государственных стандартов среднего профессионального образования (ФГОС СПО) нового поколения.
Принципиальное отличие нового стандарта в том, что в его основу положены не предметные, а ценностные ориентиры. В качестве ключевого понятия современного образования выдвигается понятие компетенций, а их формирование заявлено как одна из главных целей профессионального обучения.
Поэтому в содержании профессионального образования именно модуль как новая структурная единица занимает центральное место, поскольку требования к результатам обучения формулируются как перечень видов профессиональной деятельности и соответствующих профессиональных компетенций.
Концепции технологии модульного обучения берут свое начало в работах Б.Ф. Скиннера и трансформируют свое методологическое обоснование и профиликацию в трудах зарубежных теоретиков Б.М. Гольдшмид, К. Курха, Д.Г. Оуенса, Дж. Расселла.
Консигнатором к внедрению технологии модульного обучения явилась конференция специализированного учреждения Организации Объединённых Наций по вопросам образования, науки и культура (ЮНЕСКО), состоявшееся в Париже в 1974 году, в содержании резолюции содержалась следующая рекомендация: «создание открытых и гибких структур образования и профессионального обучения, позволяющих приспосабливаться к изменяющимся потребностям производства, науки, а также адаптироваться к местным условиям». Данному международному призыву соответствовало модульное обучение.
Модуль по теме «Неопределенный интеграл» для дисциплины «Математика» должен включать в себя:
- теоретический материал (лекция по теме курса);
- контрольные вопросы для самопроверки;
- примеры решения задач;
- задачи для самостоятельного решения;
- итоговое тестирование;
- систему оценивания;
- дополнительную литературу;
- словарь или справочник основных понятий и определений;
- табличка-памятка основных интегралов и методов интегрирования.
Цели и задачи освоения модуля.
Самостоятельное изучение темы «Неопределенный интеграл», его основных понятий, свойств, овладение основными методами интегрирования и применением их на практике, отработка вычисления табличных интегралов.
Основные виды занятий.
Самостоятельное изучение лекции на тему «Неопределенный интеграл», ответы на контрольные вопросы, рассмотрение примеров с развернутым ответом, выполнение блока заданий для самостоятельного решения, тестирование.
В качестве примера представлен фрагмент лекции на тему «Неопределенный интеграл».
«Определение. Совокупность всех первообразных функции f(x) на данном промежутке называют неопределенным интегралом от функции f(x) и обозначают ![]() , при этом f(x) называют подынтегральной функцией, выражение f(x) dx – подынтегральным, а переменной интегрирования является x.
, при этом f(x) называют подынтегральной функцией, выражение f(x) dx – подынтегральным, а переменной интегрирования является x.
Итак, ![]() f(x).
f(x).
Теорема (о существовании неопределенного интеграла). Если функция f(x) непрерывна на некотором промежутке, то для нее на этом промежутке существует первообразная, а следовательно, и неопределенный интеграл.
Геометрическая интерпретация неопределенного интеграла.
Неопределенный интеграл представляет собой семейство параллельно расположенных кривых F(x)+C, где каждому конкретному числовому значению постоянной C соответствует определенная кривая из указанного семейства.
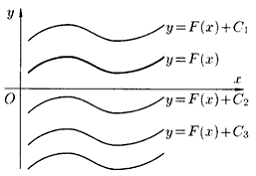
интегральной кривой.
Теорема 3. Каждая непрерывная на промежутке (a;b) функция, имеет на этом интервале первообразную.
Основные свойства неопределенного интеграла.
1) ![]() ;
;
2) ![]() ;
;
3)![]() где
где ![]() – константа, т.е. постоянный множитель можно выносить за знак неопределенного интеграла;
– константа, т.е. постоянный множитель можно выносить за знак неопределенного интеграла;
4)![]() , т.е. неопределенный интеграл от алгебраической суммы непрерывных на некоторым промежутке функций равен алгебраической сумме интегралов от каждой слагаемой функции.
, т.е. неопределенный интеграл от алгебраической суммы непрерывных на некоторым промежутке функций равен алгебраической сумме интегралов от каждой слагаемой функции.
Доказательство.
![]() .
.
![]() .
.
Пусть ![]() – первообразная для функции
– первообразная для функции ![]() . Из свойств производной, что
. Из свойств производной, что ![]() является первообразной для функции
является первообразной для функции ![]() .
.
Тогда
Так как ![]() и
и ![]() – произвольные константы, то
– произвольные константы, то ![]() – тоже произвольная константа. Поэтому, правые, а, значит, и левые части в равенствах (1) и (2) равны.
– тоже произвольная константа. Поэтому, правые, а, значит, и левые части в равенствах (1) и (2) равны.
Пусть ![]() – первообразная для функции
– первообразная для функции ![]() ; Ц(x) – первообразная для
; Ц(x) – первообразная для ![]() . Тогда
. Тогда ![]() Ц(x) – первообразная для
Ц(x) – первообразная для ![]() . Поэтому выполняется равенство
. Поэтому выполняется равенство
Так как ![]() ,
, ![]() ,
, ![]() – произвольные константы, то в равенствах (3) и (4) правые, а, значит, и левые части равны.
– произвольные константы, то в равенствах (3) и (4) правые, а, значит, и левые части равны.
Первые два свойства неопределенного интеграла говорят о том, что дифференцирование и интегрирование – взаимно обратные операции. Третье и четвертое свойства означают, то операция интегрирования линейна. Свойства (1), (3) и (4) используют для вычисления интегралов».
Если учесть тот факт, что «Математика» является одной из важнейших образовательных дисциплин, то при организации самостоятельной работы обучающихся тестирование является одной из наиболее технологичных форм проведения автоматизированного контроля с управляемыми параметрами качества. В этом плане ни одна из известных форм контроля знаний учащихся с тестированием сравниться не может. ТКТ (технология компьютерного тестирования) позволяет обеспечить эффективный предварительный, текущий, тематический и итоговый контроль знаний, умений, учет успеваемости, академических достижений. Сильной стороной тестового контроля знаний является возможность охватить в процессе тестирования большой объем материала и тем самым получить действительно широкое представление о знаниях тестируемого студента. Использование тестирования в реальной педагогической деятельности позволяет заметно повысить объективность, детальность и точность оценивания результатов процесса обучения.
В совокупности технологии модульного и тестового обучения, опираясь на их основные принципы и характеристики, дают возможность самостоятельной и правильной организации современного учебного процесса, формируют самоконтроль у студентов, являются заместителем традиционного обучения и ведущим средством повышения качества самостоятельной работы студента.
Таким образом, результатами внедрения в учебно-воспитательный процесс образовательных организаций высшего образования технологий профессионально ориентированного обучения являются:
повышение уровня сформированности основ профессиональной культуры, компетентности, конкурентоспособности специалиста (выпускника);
развитие его социальной, служебной и профессиональной мобильности; развитие научно-исследовательской и методической компетенций преподавателей.
На основании всего вышеизложенного можно сделать вывод о том, что без описанных технологий (а частности, технологии модульного обучения) существование модуля в рамках темы «Неопределенный интеграл» просто невозможно.
Стоит заметить еще тот факт, что данные технологии могут применяться также при создании модулей, затрагивающих любые другие темы из курса высшей математики, и не только математики, ну и других дисциплин.
Библиографический список
- Технология и методика профессионально ориентированного обучения : учебное пособие / под ред. Н. В. Сердюк ; [Н. В. Сердюк и др.]. – М. : Академия управления МВД России, 2019. – 64 с
- Жукова Г.С., Никитина Н.И., Комарова Е.В. Ж 86 Технологии профессионально-ориентированного обучения: учеб. пособие. – М.: Издательство РГСУ, 2012. – 165 с
- Принципы модульного обучения. Методическая разработка для преподавателе http://elib.sfu-kras.ru/bitstream/handle/2311/1416/m_moduledu.pdf?sequence=1&isAllowed=y
- Тестирование как технология контроля качества самостоятельной работы студента. Электронный научный журнал «Современные проблемы науки и образования» https://science-education.ru/ru/article/view?id=10685
- ИННОВАЦИОННЫЙ КОМПЕТЕНТНОСТНЫЙ МОДУЛЬНЫЙ ПОДХОД И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В ПРЕПОДАВАНИИ ВУЗОВСКОГО КУРСА МАТЕМАТИКИ [Электронный ресурс] // CYBERLENINKA https://cyberleninka.ru/article/n/innovatsionnyy-kompetentnostnyy-modulnyy-podhod-i-informatsionnye-tehnologii-v-prepodavanii-vuzovskogo-kursa-matematiki
- МОДУЛЬНОЕ ОБУЧЕНИЕ КАК МЕТОДИЧЕСКАЯ ОСНОВА КОНСТРУИРОВАНИЯ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ ВЫСШЕГО ОБРАЗОВАНИЯ https://cyberleninka.ru/article/n/modulnoe-obuchenie-kak-metodicheskaya-osnova-konstruirovaniya-obrazovatelnyh-programm-vysshego-obrazovaniya
- Глава пятая. Парижская мирная конференция/ история дипломатии http://art-of-diplomacy.ru/books/item/f00/s00/z0000007/st006.shtml
- МОДУЛЬНОЕ ОБУЧЕНИЕ МАТЕМАТИКЕ ПРИ ФОРМИРОВАНИИ ПРОФЕССИОНАЛЬНОЙ КОМПЕТЕНТНОСТИ СПЕЦИАЛИСТА» (https://elibrary.ru/download/elibrary_16860929_52953469.pdf
- Наиболее волнующие проблемы современного российского образования» http://e-notabene.ru/pr/article_519.html
- МОДУЛЬНОЕ ОБУЧЕНИЕ В СТРУКТУРЕ КУРСА ВЫСШЕЙ МАТЕМАТИКИ https://elibrary.ru/download/elibrary_26063320_29257333.PDF
- Модульная технология как один из путей повышения эффективности учебно-воспитательного процесса http://old.iro.yar.ru/resource/distant/society_sciense/katsch/kat2.htm
